Comment trouver la longueur d'un vecteur connaissant ses coordonnées. Vecteurs pour les nuls. Actions avec des vecteurs. Coordonnées vectorielles. Les problèmes les plus simples avec les vecteurs

10.10.2019

Comment trouver la longueur d'un vecteur ?

Afin de dériver une formule pour calculer la longueur d'un vecteur arbitraire étant donné ses coordonnées, considérons le problème suivant :

Exemple 1

Étant donné : vecteur $\overline(α)$ de coordonnées $(x,y)$. Trouver : la longueur de ce vecteur.

Introduisons un système de coordonnées cartésiennes $xOy$ sur le plan. Mettons de côté $\overline(OA)=\overline(a)$ des origines du système de coordonnées introduit. Construisons les projections $OA_1$ et $OA_2$ du vecteur construit sur les axes $Ox$ et $Oy$, respectivement (Fig. 3).

Le vecteur $\overline(OA)$ que nous avons construit sera le rayon vecteur du point $A$, il aura donc les coordonnées $(x,y)$, ce qui signifie

$=x$, $[OA_2]=y$

Maintenant, nous pouvons facilement trouver la longueur requise en utilisant le théorème de Pythagore, nous obtenons

$|\overline(α)|^2=^2+^2$

$|\overline(α)|^2=x^2+y^2$

$|\overline(α)|=\sqrt(x^2+y^2)$

Réponse : $\sqrt(x^2+y^2)$.

Conclusion: Pour trouver la longueur d'un vecteur dont les coordonnées sont données, il faut trouver la racine du carré de la somme de ces coordonnées.

Exemples de tâches

Exemple 2

Trouvez la distance entre les points $X$ et $Y$, qui ont les coordonnées suivantes : $(-1,5)$ et $(7,3)$, respectivement.

Deux points quelconques peuvent être facilement associés au concept de vecteur. Considérons, par exemple, le vecteur $\overline(XY)$. Comme nous le savons déjà, les coordonnées d'un tel vecteur peuvent être trouvées en soustrayant les coordonnées correspondantes du point de départ ($X$) des coordonnées du point final ($Y$). Nous obtenons cela

Depuis nos années d'école, nous savons ce que c'est vecteur est un segment qui a une direction et se caractérise par valeur numérique paire de points ordonnée. Le nombre égal à la longueur du segment qui sert de base est défini comme longueur du vecteur . Pour le définir, nous utiliserons système de coordonnées. Nous prenons également en compte une autre caractéristique - direction du segment . Pour trouver la longueur d’un vecteur, vous pouvez utiliser deux méthodes. Le plus simple est de prendre une règle et de mesurer ce que ce sera. Ou vous pouvez utiliser la formule. Nous allons maintenant considérer cette option.

Nécessaire:

— système de coordonnées (x, y);
— vecteur ;
- connaissance de l'algèbre et de la géométrie.

Instructions:

Formule pour déterminer la longueur d'un segment dirigéécrivons-le comme suit r²= x²+y². En prenant la racine carrée de r² et le nombre résultant sera le résultat. Pour trouver la longueur d’un vecteur, nous effectuons les étapes suivantes. Nous désignons le point de départ des coordonnées (x1;y1), point final (x2;y2). Nous trouvons X Et oui par la différence entre les coordonnées de fin et de début du segment orienté. Autrement dit, le nombre (X) déterminé par la formule suivante x=x2-x1, et le numéro (o) respectivement y=y2-y1.
Trouvez le carré de la somme des coordonnées à l'aide de la formule x²+y². On extrait la racine carrée du nombre résultant, qui sera la longueur du vecteur (r). La solution au problème posé sera simplifiée si les données initiales des coordonnées du segment orienté sont immédiatement connues. Tout ce que vous avez à faire est d’insérer les données dans la formule.
Attention! Le vecteur ne peut pas être sur le plan de coordonnées, mais dans l'espace, auquel cas une valeur supplémentaire sera ajoutée à la formule, et il aura vue suivante: r²= x²+y²+ z², Où - (z) un axe supplémentaire qui permet de déterminer la taille d'un segment dirigé dans l'espace.

J’ai enfin mis la main sur ce sujet vaste et tant attendu. géométrie analytique. Tout d'abord, un peu sur cette section mathématiques supérieures…. Vous vous souvenez sûrement maintenant d'un cours de géométrie scolaire avec de nombreux théorèmes, leurs preuves, dessins, etc. De quoi cacher, un sujet mal-aimé et souvent obscur pour une partie importante des étudiants. Curieusement, la géométrie analytique peut sembler plus intéressante et plus accessible. Que signifie l’adjectif « analytique » ? Deux expressions mathématiques clichées me viennent immédiatement à l’esprit : « méthode de solution graphique » et « méthode de solution analytique ». Méthode graphique , bien sûr, est associé à la construction de graphiques et de dessins. Analytique même méthode implique de résoudre des problèmes principalementà travers des opérations algébriques. À cet égard, l'algorithme permettant de résoudre presque tous les problèmes de géométrie analytique est simple et transparent ; il suffit souvent d'appliquer soigneusement les formules nécessaires - et la réponse est prête ! Non, bien sûr, nous ne pourrons pas faire cela sans dessins du tout, et d'ailleurs, pour une meilleure compréhension de la matière, j'essaierai de les citer au-delà de la nécessité.

Le nouveau cours de géométrie ne prétend pas être théoriquement complet ; il est axé sur la résolution de problèmes pratiques. J'inclurai dans mes cours uniquement ce qui, de mon point de vue, est important en termes pratiques. Si vous avez besoin d'une aide plus complète sur une sous-section, je recommande la littérature suivante assez accessible :

1) Une chose que, sans blague, plusieurs générations connaissent bien : Manuel scolaire de géométrie, auteurs - L.S. Atanasyan et compagnie. Ce cintre de vestiaire scolaire a déjà fait l'objet de 20 (!) réimpressions, ce qui, bien sûr, n'est pas la limite.

2) Géométrie en 2 volumes. Auteurs L.S. Atanasyan, Bazylev V.T.. C'est de la littérature pour lycée, Tu auras besoin de premier tome. Des tâches rarement rencontrées peuvent tomber hors de ma vue, et Didacticiel apportera une aide précieuse.

Les deux livres peuvent être téléchargés gratuitement en ligne. De plus, vous pouvez utiliser mes archives avec solutions toutes faites, que l'on peut trouver sur la page Télécharger des exemples en mathématiques supérieures.

Parmi les outils, je propose à nouveau mon propre développement - progiciel en géométrie analytique, ce qui simplifiera grandement la vie et fera gagner beaucoup de temps.

Il est supposé que le lecteur connaît les concepts et figures géométriques de base : point, droite, plan, triangle, parallélogramme, parallélépipède, cube, etc. Il convient de rappeler certains théorèmes, au moins le théorème de Pythagore, bonjour les répétiteurs)

Et maintenant, nous allons considérer séquentiellement : la notion de vecteur, les actions avec des vecteurs, les coordonnées vectorielles. Je recommande de lire plus loin l'article le plus important Produit scalaire des vecteurs, et aussi Vecteur et produit mixte de vecteurs. Une tâche locale - la division d'un segment à cet égard - ne sera pas non plus superflue. Sur la base des informations ci-dessus, vous pouvez maîtriser équation d'une droite dans un plan Avec exemples de solutions les plus simples, ce qui permettra apprendre à résoudre des problèmes de géométrie. Les articles suivants sont également utiles : Équation d'un avion dans l'espace, Équations d'une droite dans l'espace, Problèmes de base sur une droite et un plan, autres sections de géométrie analytique. Naturellement, des tâches standards seront prises en compte en cours de route.

Notion de vecteur. Vecteur libre

Tout d’abord, répétons la définition scolaire d’un vecteur. Vecteur appelé dirigé un segment pour lequel son début et sa fin sont indiqués :

DANS dans ce cas le début du segment est le point, la fin du segment est le point. Le vecteur lui-même est noté . Direction est essentiel, si vous déplacez la flèche à l'autre extrémité du segment, vous obtenez un vecteur, et c'est déjà vecteur complètement différent. Le concept de vecteur est commodément identifié au mouvement corps physique: D'accord, franchir les portes de l'institut ou sortir des portes de l'institut sont des choses complètement différentes.

Il est pratique de considérer les points individuels d'un plan ou d'un espace comme ce qu'on appelle vecteur zéro. Pour un tel vecteur, la fin et le début coïncident.

!!! Note: Ici et plus loin, vous pouvez supposer que les vecteurs se trouvent dans le même plan ou vous pouvez supposer qu'ils sont situés dans l'espace - l'essence du matériau présenté est valable à la fois pour le plan et pour l'espace.

Désignations : Beaucoup ont immédiatement remarqué le bâton sans flèche dans la désignation et ont dit : il y a aussi une flèche en haut ! C'est vrai, on peut l'écrire avec une flèche : , mais c'est aussi possible l'entrée que j'utiliserai à l'avenir. Pourquoi? Apparemment, cette habitude s'est développée pour des raisons pratiques : mes tireurs à l'école et à l'université se sont révélés trop différents et hirsutes. Dans la littérature pédagogique, parfois ils ne s'embarrassent pas du tout de l'écriture cunéiforme, mais mettent en évidence les lettres en gras : , ce qui implique qu'il s'agit d'un vecteur.

C'était de la stylistique, et maintenant des façons d'écrire des vecteurs :

1) Les vecteurs peuvent être écrits en deux lettres latines majuscules :
et ainsi de suite. Dans ce cas, la première lettre Nécessairement désigne le point de départ du vecteur et la deuxième lettre désigne le point final du vecteur.

2) Les vecteurs s'écrivent aussi en petites lettres latines :
En particulier, notre vecteur peut être redésigné par souci de concision par une petite lettre latine.

Longueur ou module un vecteur non nul est appelé la longueur du segment. La longueur du vecteur zéro est nulle. Logique.

La longueur du vecteur est indiquée par le signe du module : ,

Nous apprendrons comment trouver la longueur d'un vecteur (ou nous le répéterons, selon qui) un peu plus tard.

Il s’agissait d’informations de base sur les vecteurs, familières à tous les écoliers. En géométrie analytique, ce qu'on appelle vecteur libre.

Pour le dire simplement - le vecteur peut être tracé à partir de n'importe quel point:

Nous avons l'habitude d'appeler de tels vecteurs égaux (la définition des vecteurs égaux sera donnée ci-dessous), mais d'un point de vue purement mathématique, ce sont le MÊME VECTEUR ou vecteur libre. Pourquoi gratuit ? Car au cours de la résolution de problèmes, vous pouvez « attacher » tel ou tel vecteur à N'IMPORTE QUEL point du plan ou de l'espace dont vous avez besoin. C'est une fonctionnalité très intéressante ! Imaginez un vecteur de longueur et de direction arbitraires - il peut être « cloné » un nombre infini de fois et à n'importe quel point de l'espace, en fait, il existe PARTOUT. Il y a un tel étudiant qui dit : tous les professeurs se soucient du vecteur. Après tout, ce n'est pas seulement une rime pleine d'esprit, tout est mathématiquement correct - le vecteur peut également y être attaché. Mais ne vous précipitez pas pour vous réjouir, ce sont souvent les étudiants eux-mêmes qui en souffrent =)

Donc, vecteur libre- Ce un tas de segments orientés identiques. La définition scolaire d'un vecteur, donnée au début du paragraphe : « Un segment orienté est appelé vecteur... », implique spécifique segment dirigé tiré de ensemble donné, qui est lié à un point spécifique du plan ou de l’espace.

Il convient de noter que du point de vue de la physique, le concept de vecteur libre est généralement incorrect et que le point d'application du vecteur compte. En effet, un coup direct de la même force sur le nez ou le front, suffisant pour développer mon stupide exemple, entraîne des conséquences différentes. Cependant, non libre des vecteurs se trouvent également au cours de vyshmat (n'y allez pas :)).

Actions avec des vecteurs. Colinéarité des vecteurs

DANS cours scolaire géométrie, un certain nombre d'actions et de règles avec des vecteurs sont considérées : addition selon la règle du triangle, addition selon la règle du parallélogramme, règle de différence vectorielle, multiplication d'un vecteur par un nombre, produit scalaire de vecteurs, etc. Pour commencer, répétons deux règles particulièrement pertinentes pour résoudre des problèmes de géométrie analytique.

La règle pour ajouter des vecteurs à l'aide de la règle du triangle

Considérons deux vecteurs arbitraires non nuls et :

Vous devez trouver la somme de ces vecteurs. Etant donné que tous les vecteurs sont considérés comme libres, nous mettrons de côté le vecteur de fin vecteur:

La somme des vecteurs est le vecteur. Pour une meilleure compréhension de la règle, il convient de lui donner une signification physique : laisser un corps se déplacer le long du vecteur , puis le long du vecteur . Ensuite, la somme des vecteurs est le vecteur du chemin résultant avec le début au point de départ et la fin au point d'arrivée. Une règle similaire est formulée pour la somme d’un nombre quelconque de vecteurs. Comme on dit, le corps peut parcourir son chemin très penché en zigzag, ou peut-être en pilote automatique - le long du vecteur résultant de la somme.

D'ailleurs, si le vecteur est reporté de commencé vecteur, alors on obtient l'équivalent règle du parallélogramme ajout de vecteurs.

Premièrement, à propos de la colinéarité des vecteurs. Les deux vecteurs sont appelés colinéaire, s'ils se trouvent sur la même ligne ou sur des lignes parallèles. En gros, nous parlons de vecteurs parallèles. Mais à leur égard, l'adjectif « colinéaire » est toujours utilisé.

Imaginez deux vecteur colinéaire. Si les flèches de ces vecteurs sont dirigées dans la même direction, alors ces vecteurs sont appelés co-dirigé. Si les flèches pointent vers différents côtés, alors les vecteurs seront directions opposées.

Désignations : la colinéarité des vecteurs s'écrit avec le symbole de parallélisme habituel : , tandis que le détail est possible : (les vecteurs sont co-dirigés) ou (les vecteurs sont dirigés de manière opposée).

Le travail un vecteur non nul sur un nombre est un vecteur dont la longueur est égale à , et les vecteurs et sont co-dirigés vers et dirigés de manière opposée vers .

La règle pour multiplier un vecteur par un nombre est plus facile à comprendre à l'aide d'une image :

Regardons cela plus en détail :

1 direction. Si le multiplicateur est négatif, alors le vecteur change de direction au contraire.

2) Longueur. Si le multiplicateur est contenu dans ou , alors la longueur du vecteur diminue. Ainsi, la longueur du vecteur est la moitié de la longueur du vecteur. Si le module du multiplicateur est supérieur à un, alors la longueur du vecteur augmenteà l'heure.

3) Veuillez noter que tous les vecteurs sont colinéaires, tandis qu'un vecteur est exprimé à travers un autre, par exemple . L'inverse est également vrai: si un vecteur peut être exprimé par un autre, alors ces vecteurs sont nécessairement colinéaires. Ainsi: si on multiplie un vecteur par un nombre, on obtient colinéaire(par rapport à l'original) vecteur.

4) Les vecteurs sont co-dirigés. Les vecteurs et sont également co-dirigés. Tout vecteur du premier groupe est dirigé de manière opposée par rapport à tout vecteur du deuxième groupe.

Quels vecteurs sont égaux ?

Deux vecteurs sont égaux s’ils vont dans la même direction et ont la même longueur. Notez que la codirectionnalité implique la colinéarité des vecteurs. La définition serait inexacte (redondante) si l’on disait : « Deux vecteurs sont égaux s’ils sont colinéaires, codirectionnels et ont la même longueur. »

Du point de vue du concept de vecteur libre, les vecteurs égaux sont le même vecteur, comme indiqué dans le paragraphe précédent.

Coordonnées vectorielles dans le plan et dans l'espace

Le premier point est de considérer les vecteurs sur le plan. Représentons un système de coordonnées rectangulaires cartésiennes et traçons-le à partir de l'origine des coordonnées célibataire vecteurs et :

Vecteurs et orthogonal. Orthogonal = Perpendiculaire. Je vous recommande de vous habituer petit à petit aux termes : au lieu de parallélisme et perpendiculaire, on utilise respectivement les mots colinéarité Et orthogonalité.

Désignation: L'orthogonalité des vecteurs s'écrit avec le symbole habituel de perpendiculaire, par exemple : .

Les vecteurs considérés sont appelés vecteurs de coordonnées ou orts. Ces vecteurs forment base en surface. Ce qu'est une base, je pense, est intuitivement clair pour beaucoup, plus des informations détaillées peut être trouvé dans l'article Dépendance linéaire (non) des vecteurs. Base des vecteurs En termes simples, la base et l'origine des coordonnées définissent l'ensemble du système - c'est une sorte de fondement sur lequel bout une vie géométrique pleine et riche.

Parfois, la base construite est appelée orthonormé base du plan : « ortho » - parce que les vecteurs de coordonnées sont orthogonaux, l'adjectif « normalisé » signifie unité, c'est-à-dire les longueurs des vecteurs de base sont égales à un.

Désignation: la base est généralement écrite entre parenthèses, à l'intérieur desquelles dans un ordre strict les vecteurs de base sont répertoriés, par exemple : . Coordonner les vecteurs c'est interdit réarranger.

N'importe lequel vecteur d'avion Le seul moyen exprimé comme suit :
, Où - Nombres qui sont appelés coordonnées vectorielles dans cette base. Et l'expression elle-même appelé décomposition vectoriellepar base .

Dîner servi :

Commençons par la première lettre de l'alphabet : . Le dessin montre clairement que lors de la décomposition d'un vecteur en base, ceux qui viennent d'être discutés sont utilisés :
1) la règle pour multiplier un vecteur par un nombre : et ;
2) addition de vecteurs selon la règle du triangle : .

Tracez maintenant mentalement le vecteur à partir de n’importe quel autre point du plan. Il est bien évident que sa déchéance « le suivra sans relâche ». La voici, la liberté du vecteur - le vecteur « porte tout avec lui ». Bien entendu, cette propriété est vraie pour tout vecteur. C'est drôle que les vecteurs de base (libres) eux-mêmes n'aient pas besoin d'être tracés à partir de l'origine ; l'un peut être dessiné, par exemple, en bas à gauche, et l'autre en haut à droite, et rien ne changera ! Certes, vous n’avez pas besoin de le faire, puisque le professeur fera également preuve d’originalité et vous tirera un « crédit » dans un endroit inattendu.

Les vecteurs illustrent exactement la règle de multiplication d'un vecteur par un nombre, le vecteur est codirectionnel avec le vecteur de base, le vecteur est dirigé à l'opposé du vecteur de base. Pour ces vecteurs, une des coordonnées est égale à zéro, vous pouvez l'écrire minutieusement comme ceci :

Et les vecteurs de base, d'ailleurs, sont comme ceci : (en fait, ils s'expriment par eux-mêmes).

Et enfin: , . Au fait, qu’est-ce que la soustraction vectorielle et pourquoi n’ai-je pas parlé de la règle de soustraction ? Quelque part en algèbre linéaire, je ne sais plus où, j'ai remarqué que la soustraction est cas particulier ajout. Ainsi, les développements des vecteurs « de » et « e » s'écrivent facilement sous la forme d'une somme : , . Réorganisez les termes et voyez sur le dessin à quel point la bonne vieille addition de vecteurs selon la règle du triangle fonctionne dans ces situations.

La décomposition considérée de la forme parfois appelé décomposition vectorielle dans le système ort(c'est-à-dire dans un système de vecteurs unitaires). Mais ce n’est pas la seule façon d’écrire un vecteur ; l’option suivante est courante :

Ou avec un signe égal :

Les vecteurs de base eux-mêmes s'écrivent comme suit : et

C'est-à-dire que les coordonnées du vecteur sont indiquées entre parenthèses. Dans les problèmes pratiques, les trois options de notation sont utilisées.

Je doutais de parler, mais je le dis quand même : les coordonnées vectorielles ne peuvent pas être réorganisées. Strictement en première place on note la coordonnée qui correspond au vecteur unitaire, strictement en deuxième position on note la coordonnée qui correspond au vecteur unitaire. En effet, et ce sont deux vecteurs différents.

Nous avons trouvé les coordonnées dans l'avion. Regardons maintenant les vecteurs dans l'espace tridimensionnel, presque tout est pareil ici ! Cela ajoutera simplement une coordonnée supplémentaire. Il est difficile de réaliser des dessins en trois dimensions, je me limiterai donc à un seul vecteur, que par simplicité je mettrai de côté de l'origine :

N'importe lequel Vecteur spatial 3D Le seul moyen développer sur une base orthonormée :
, où sont les coordonnées du vecteur (nombre) dans cette base.

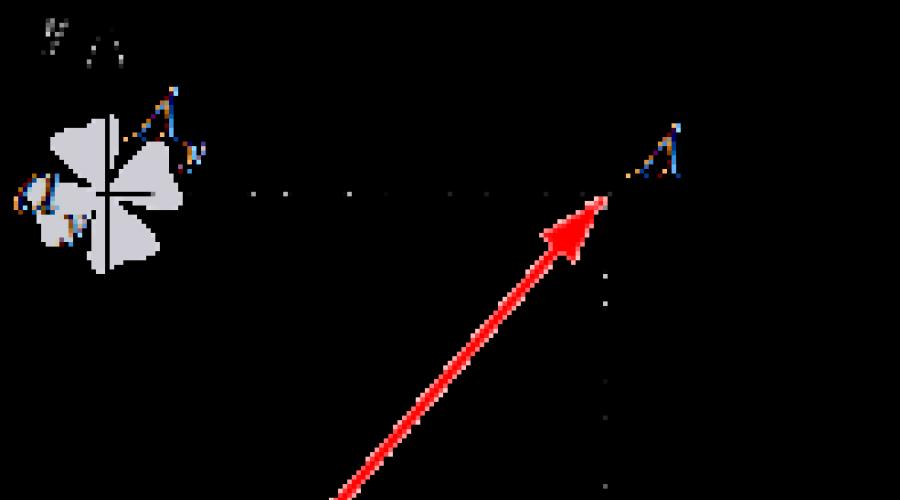
Exemple tiré de l'image : . Voyons comment fonctionnent les règles vectorielles ici. Tout d’abord, multipliez le vecteur par un nombre : (flèche rouge), (flèche verte) et (flèche framboise). Deuxièmement, voici un exemple d'ajout de plusieurs, dans ce cas de trois, vecteurs : . Le vecteur somme commence au point de départ initial (début du vecteur) et se termine au point d'arrivée final (fin du vecteur).

Naturellement, tous les vecteurs de l'espace tridimensionnel sont également libres ; essayez de séparer mentalement le vecteur de tout autre point, et vous comprendrez que sa décomposition « restera avec lui ».

Semblable au boîtier plat, en plus d'écrire les versions avec parenthèses sont largement utilisées : soit .

S'il manque un (ou deux) vecteurs de coordonnées dans le développement, alors des zéros sont mis à leur place. Exemples:
vecteur (méticuleusement ) - écrivons ;
vecteur (méticuleusement ) - écrivons ;
vecteur (méticuleusement ) - écrivons .

Les vecteurs de base s'écrivent comme suit :

C'est peut-être là toutes les connaissances théoriques minimales nécessaires pour résoudre les problèmes de géométrie analytique. Il peut y avoir beaucoup de termes et de définitions, je recommande donc aux théières de relire et de comprendre à nouveau ces informations. Et il sera utile à tout lecteur de se référer de temps en temps à la leçon de base pour mieux assimiler la matière. Colinéarité, orthogonalité, base orthonormée, décomposition vectorielle - ces concepts et d'autres seront souvent utilisés à l'avenir. Je tiens à préciser que les matériaux du site ne suffisent pas pour réussir un test théorique ou un colloque de géométrie, puisque je crypte soigneusement tous les théorèmes (et sans preuves) - au détriment de style scientifique présentation, mais un plus pour votre compréhension du sujet. Pour recevoir des informations théoriques détaillées, veuillez vous incliner devant le professeur Atanasyan.

Et on passe à la partie pratique :

Les problèmes les plus simples de géométrie analytique.
Actions avec des vecteurs en coordonnées

Il est fortement conseillé d'apprendre à résoudre les tâches qui seront prises en compte de manière entièrement automatique, ainsi que les formules mémoriser, ne vous en souvenez même pas spécifiquement, ils se souviendront d'eux-mêmes =) C'est très important, car dans le plus simple exemples élémentaires d'autres problèmes de géométrie analytique reposent, et il serait dommage de passer plus de temps à manger des pions. Il n'est pas nécessaire de fermer les boutons du haut de votre chemise ; beaucoup de choses vous sont familières depuis l'école.

La présentation du matériel suivra un parcours parallèle - tant pour l'avion que pour l'espace. Parce que toutes les formules... vous le constaterez par vous-même.

Comment trouver un vecteur à partir de deux points ?

Si deux points du plan et sont donnés, alors le vecteur a les coordonnées suivantes :

Si deux points dans l'espace et sont donnés, alors le vecteur a les coordonnées suivantes :

C'est, à partir des coordonnées de la fin du vecteur vous devez soustraire les coordonnées correspondantes début du vecteur.

Exercice: Pour les mêmes points, notez les formules pour trouver les coordonnées du vecteur. Formules en fin de cours.

Exemple 1

Étant donné deux points du plan et . Trouver des coordonnées vectorielles

Solution: selon la formule appropriée :

Alternativement, l'entrée suivante pourrait être utilisée :

Les esthètes en décideront :

Personnellement, je suis habitué à la première version de l'enregistrement.

Répondre:

Selon la condition, il n'était pas nécessaire de construire un dessin (ce qui est typique des problèmes de géométrie analytique), mais afin de clarifier certains points pour les nuls, je ne serai pas paresseux :

Tu dois absolument comprendre différence entre les coordonnées du point et les coordonnées vectorielles:

Coordonnées des points– ce sont des coordonnées ordinaires dans un système de coordonnées rectangulaires. Je pense que tout le monde sait tracer des points sur un plan de coordonnées de la 5e à la 6e année. Chaque point a une place stricte dans l'avion et ne peut être déplacé nulle part.

Les coordonnées du vecteur– c'est son expansion selon la base, dans ce cas. Tout vecteur est libre, donc si nécessaire, nous pouvons facilement l'éloigner d'un autre point du plan. Il est intéressant de noter que pour les vecteurs, vous n’avez pas du tout besoin de construire des axes ou un système de coordonnées rectangulaires ; vous avez seulement besoin d’une base, dans ce cas une base orthonormée du plan ;

Les enregistrements de coordonnées de points et de coordonnées de vecteurs semblent être similaires : , et signification des coordonnées absolument différent, et vous devriez être bien conscient de cette différence. Bien entendu, cette différence s’applique également à l’espace.

Mesdames et messieurs, remplissons nos mains :

Exemple 2

a) Les points et sont attribués. Trouver des vecteurs et .
b) Les points sont attribués Et . Trouver des vecteurs et .
c) Les points et sont attribués. Trouver des vecteurs et .
d) Des points sont attribués. Trouver des vecteurs .

C'est peut-être suffisant. Ce sont des exemples pour décision indépendante, essayez de ne pas les négliger, cela sera payant ;-). Il n'est pas nécessaire de faire des dessins. Solutions et réponses à la fin de la leçon.

Qu'est-ce qui est important lors de la résolution de problèmes de géométrie analytique ? Il est important d’être EXTRÊMEMENT PRUDENT pour éviter de commettre l’erreur magistrale « deux plus deux égale zéro ». Je m'excuse tout de suite si j'ai fait une erreur quelque part =)

Comment trouver la longueur d'un segment ?

La longueur, comme déjà noté, est indiquée par le signe du module.

Si deux points du plan sont donnés et , alors la longueur du segment peut être calculée à l'aide de la formule

Si deux points dans l'espace et sont donnés, alors la longueur du segment peut être calculée à l'aide de la formule

Note: Les formules resteront correctes si les coordonnées correspondantes sont interverties : et , mais la première option est plus standard

Exemple 3

Solution: selon la formule appropriée :

Répondre:

Pour plus de clarté, je vais faire un dessin

Segment de ligne - ce n'est pas un vecteur, et bien sûr, vous ne pouvez le déplacer nulle part. De plus, si vous dessinez à l'échelle : 1 unité. = 1 cm (deux cellules de cahier), alors la réponse obtenue peut être vérifiée avec une règle ordinaire en mesurant directement la longueur du segment.

Oui, la solution est courte, mais elle en contient quelques autres les points importants que je voudrais clarifier:

Tout d'abord, dans la réponse nous mettons la dimension : « unités ». La condition ne dit pas de quoi il s’agit, millimètres, centimètres, mètres ou kilomètres. Par conséquent, une solution mathématiquement correcte serait la formulation générale : « unités » – abrégé en « unités ».

Deuxièmement, répétons le matériel scolaire, qui est utile non seulement pour la tâche considérée :

faire attention à technique importante – retirer le multiplicateur sous la racine. À la suite des calculs, nous obtenons un résultat et un bon style mathématique consiste à supprimer le facteur sous la racine (si possible). Plus en détail, le processus ressemble à ceci : . Bien sûr, laisser la réponse telle quelle ne serait pas une erreur – mais ce serait certainement une lacune et un argument de poids pour ergoter de la part de l’enseignant.

Voici d'autres cas courants :

Il y en a souvent assez à la racine grand nombre, Par exemple . Que faire dans de tels cas ? A l'aide de la calculatrice, on vérifie si le nombre est divisible par 4 : . Oui, il était complètement divisé, ainsi : . Ou peut-être que le nombre peut à nouveau être divisé par 4 ? . Ainsi: . Le dernier chiffre du nombre est impair, donc diviser par 4 une troisième fois ne fonctionnera évidemment pas. Essayons de diviser par neuf : . Par conséquent:
Prêt.

Conclusion: si sous la racine nous obtenons un nombre qui ne peut pas être extrait dans son ensemble, alors nous essayons de supprimer le facteur sous la racine - à l'aide d'une calculatrice, nous vérifions si le nombre est divisible par : 4, 9, 16, 25, 36, 49, etc.

Lors de la décision diverses tâches les racines sont courantes, essayez toujours d'extraire les facteurs sous la racine afin d'éviter une note inférieure et des problèmes inutiles pour finaliser vos solutions sur la base des commentaires de l'enseignant.

Répétons également la quadrature des racines et autres puissances :

Règles pour les actions avec diplômes en vue générale peut être trouvé dans un manuel scolaire d'algèbre, mais je pense qu'à partir des exemples donnés, tout ou presque est déjà clair.

Tâche de solution indépendante avec un segment dans l'espace :

Exemple 4

Les points et sont donnés. Trouvez la longueur du segment.

La solution et la réponse se trouvent à la fin de la leçon.

Comment trouver la longueur d'un vecteur ?

Si un vecteur plan est donné, alors sa longueur est calculée par la formule.

Si un vecteur spatial est donné, alors sa longueur est calculée par la formule .

Définition 1

Un segment est une partie d'une ligne qui a deux limites sous forme de points.

Définition 2

Nous appellerons vecteur ou segment orienté un segment pour lequel on sait laquelle des limites du segment est considérée comme le début et laquelle est sa fin.

Désignation : En deux lettres : $\overline(AB)$ – (où $A$ est son début et $B$ est sa fin).

En une petite lettre : $\overline(a)$ (Fig. 1).

Introduisons maintenant directement la notion de longueurs vectorielles.

Définition 3

La longueur du vecteur $\overline(a)$ sera la longueur du segment $a$.

Notation : $|\overline(a)|$

Le concept de longueur de vecteur est associé, par exemple, à un concept tel que l'égalité de deux vecteurs.

Définition 4

Nous appellerons deux vecteurs égaux s’ils satisfont à deux conditions : 1. Ils sont codirectionnels ; 1. Leurs longueurs sont égales (Fig. 2).

Définition 5

Nous appellerons les coefficients de dilatation du vecteur $\overline(c)=m\overline(i)+n\overline(j)$ les coordonnées de ce vecteur dans le système de coordonnées introduit. Mathématiquement:

$\overline(c)=(m,n)$

Comment trouver la longueur d'un vecteur ?

Afin de dériver une formule pour calculer la longueur d'un vecteur arbitraire étant donné ses coordonnées, considérons le problème suivant :

Exemple 1

Étant donné : vecteur $\overline(α)$ de coordonnées $(x,y)$. Trouver : la longueur de ce vecteur.

Le vecteur $\overline(OA)$ que nous avons construit sera le rayon vecteur du point $A$, il aura donc les coordonnées $(x,y)$, ce qui signifie

$=x$, $[OA_2]=y$

Maintenant, nous pouvons facilement trouver la longueur requise en utilisant le théorème de Pythagore, nous obtenons

$|\overline(α)|^2=^2+^2$

$|\overline(α)|^2=x^2+y^2$

$|\overline(α)|=\sqrt(x^2+y^2)$

Réponse : $\sqrt(x^2+y^2)$.

Conclusion: Pour trouver la longueur d'un vecteur dont les coordonnées sont données, il faut trouver la racine du carré de la somme de ces coordonnées.

Exemples de tâches

Exemple 2

Trouvez la distance entre les points $X$ et $Y$, qui ont les coordonnées suivantes : $(-1,5)$ et $(7,3)$, respectivement.

Comment trouver la longueur d'un vecteur connaissant ses coordonnées. Vecteurs pour les nuls. Actions avec des vecteurs. Coordonnées vectorielles. Les problèmes les plus simples avec les vecteurs

Lire aussi

Comment trouver la longueur d'un vecteur ?

Exemples de tâches

Nécessaire:

Instructions:

Notion de vecteur. Vecteur libre

Actions avec des vecteurs. Colinéarité des vecteurs

La règle pour ajouter des vecteurs à l'aide de la règle du triangle

Quels vecteurs sont égaux ?

Coordonnées vectorielles dans le plan et dans l'espace

Les problèmes les plus simples de géométrie analytique.Actions avec des vecteurs en coordonnées

Comment trouver un vecteur à partir de deux points ?

Comment trouver la longueur d'un segment ?

Comment trouver la longueur d'un vecteur ?

Comment trouver la longueur d'un vecteur ?

Exemples de tâches

Les problèmes les plus simples de géométrie analytique.
Actions avec des vecteurs en coordonnées