Formules pour fonctions complexes. Dérivés complexes. Dérivée logarithmique. Dérivée d'une fonction puissance-exponentielle
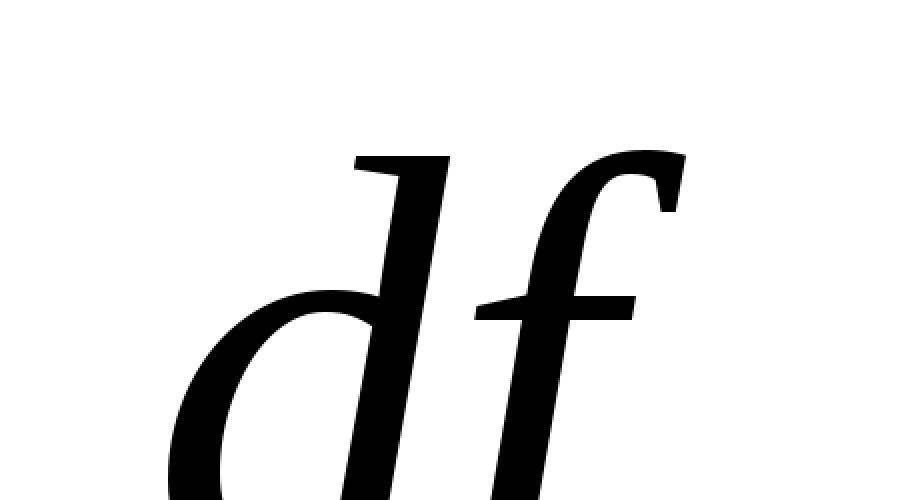
Dans les manuels « anciens », on l’appelle aussi la règle de la « chaîne ». Donc si y = f (u), et u = φ (x), c'est
y = f (φ (x))
complexe - fonction composite (composition de fonctions) alors
Où  , après calcul est considéré à u = φ (x).
, après calcul est considéré à u = φ (x).


A noter qu'ici nous avons pris des compositions « différentes » à partir des mêmes fonctions, et le résultat de la différenciation s'est naturellement avéré dépendre de l'ordre de « mélange ».
La règle de la chaîne s’étend naturellement aux compositions de trois fonctions ou plus. Dans ce cas, il y aura trois « maillons » ou plus dans la « chaîne » qui constitue le dérivé. Voici une analogie avec la multiplication : « nous avons » une table de dérivées ; "là" - table de multiplication ; « avec nous » est la règle de la chaîne et « là » est la règle de multiplication de la « colonne ». Lors du calcul de telles dérivées « complexes », aucun argument auxiliaire (u¸v, etc.), bien sûr, n'est introduit, mais, ayant noté par eux-mêmes le nombre et la séquence de fonctions impliquées dans la composition, les liens correspondants sont « enfilés » dans l'ordre indiqué.
 . Ici, avec le « x » pour obtenir la valeur du « y », cinq opérations sont effectuées, c'est-à-dire qu'il y a une composition de cinq fonctions : « externe » (la dernière d'entre elles) - exponentielle - e ; puis dans l'ordre inverse, la puissance. (♦) 2 ; péché trigonométrique(); calme. () 3 et enfin logarithmique ln.(). C'est pourquoi
. Ici, avec le « x » pour obtenir la valeur du « y », cinq opérations sont effectuées, c'est-à-dire qu'il y a une composition de cinq fonctions : « externe » (la dernière d'entre elles) - exponentielle - e ; puis dans l'ordre inverse, la puissance. (♦) 2 ; péché trigonométrique(); calme. () 3 et enfin logarithmique ln.(). C'est pourquoi
Avec les exemples suivants, nous allons « faire d'une pierre deux coups » : nous nous entraînerons à différencier des fonctions complexes et à compléter le tableau des dérivées des fonctions élémentaires. Donc:
4. Pour une fonction puissance - y = x α - réécrivez-la en utilisant la fameuse « fonction de base » identité logarithmique" - b=e ln b - sous la forme x α = x α ln x on obtient
5. Pour une fonction exponentielle arbitraire, en utilisant la même technique que nous aurons
6. Pour une fonction logarithmique arbitraire, en utilisant la formule bien connue de transition vers une nouvelle base, on obtient systématiquement
 .
.
7. Pour différencier la tangente (cotangente), on utilise la règle de différenciation des quotients :
Pour obtenir les dérivées des fonctions trigonométriques inverses, nous utilisons la relation qui est satisfaite par les dérivées de deux fonctions mutuellement inverses, c'est-à-dire les fonctions φ (x) et f (x) liées par les relations :
C'est le rapport

C'est à partir de cette formule pour les fonctions mutuellement inverses
 Et
Et  ,
,
Enfin, résumons ces dérivées et quelques autres qui sont également facilement obtenues dans le tableau suivant.
|
|
|
||
|
|
|
||
|
|
Depuis votre arrivée ici, vous avez probablement déjà vu cette formule dans le manuel
et fais une grimace comme celle-ci :
Ami, ne t'inquiète pas ! En fait, tout est tout simplement scandaleux. Vous comprendrez certainement tout. Une seule demande - lisez l'article lentement, essayez de comprendre chaque étape. J'ai écrit aussi simplement et clairement que possible, mais encore faut-il comprendre l'idée. Et assurez-vous de résoudre les tâches de l'article.
Qu'est-ce qu'une fonction complexe ?
Imaginez que vous déménagez dans un autre appartement et que vous emballez donc vos affaires dans de grandes cartons. Supposons que nous devions en collecter petits objets, par exemple, le matériel d'écriture scolaire. Si vous les jetez simplement dans une énorme boîte, ils se perdront entre autres. Pour éviter cela, vous les mettez d'abord, par exemple, dans un sac, que vous mettez ensuite dans une grande boîte, après quoi vous la scellez. Ce processus « complexe » est présenté dans le schéma ci-dessous :

Il semblerait, qu'est-ce que les mathématiques ont à voir là-dedans ? Oui, malgré le fait qu’une fonction complexe se forme EXACTEMENT DE LA MÊME manière ! Seulement, nous « emballons » non pas des cahiers et des stylos, mais des \(x\), alors que les « paquets » et les « boîtes » sont différents.
Par exemple, prenons x et « emballons-le » dans une fonction :

En conséquence, nous obtenons, bien sûr, \(\cosx\). C'est notre « sac de choses ». Maintenant, mettons-le dans une « boîte » - emballons-le, par exemple, dans une fonction cubique.

Que va-t-il se passer à la fin ? Oui, c’est vrai, il y aura un « sac de choses dans une boîte », c’est-à-dire un « cosinus de X au cube ».

La conception qui en résulte est une fonction complexe. Il diffère du simple en ce sens PLUSIEURS « impacts » (packages) sont appliqués sur un X à la suite et il s'avère que c'est « fonction à partir de la fonction » - « emballage dans l'emballage ».
DANS cours scolaire Il existe très peu de types de ces « packages », seulement quatre :

Maintenant, "emballons" X d'abord dans fonction exponentielle en base 7, puis en fonction trigonométrique. On a:
\(x → 7^x → tg(7^x)\)
Maintenant, "emballons" X deux fois dans fonctions trigonométriques, d'abord dans , puis dans :
\(x → sinx → cotg (sinx)\)
Simple, non ?
Maintenant, écrivez vous-même les fonctions, où x :
- il est d'abord « emballé » dans un cosinus, puis dans une fonction exponentielle de base \(3\) ;
- d'abord à la puissance cinquième, puis à la tangente ;
- d'abord au logarithme en base \(4\)
, puis à la puissance \(-2\).
Trouvez les réponses à cette tâche à la fin de l'article.
Pouvons-nous « emballer » X non pas deux, mais trois fois ? Aucun problème! Et quatre, cinq et vingt-cinq fois. Voici, par exemple, une fonction dans laquelle x est « compressé » \(4\) fois :
\(y=5^(\log_2(\sin(x^4)))\)
Mais de telles formules ne se retrouvent pas dans la pratique scolaire (les étudiants ont plus de chance - la leur peut être plus compliquée☺).
"Déballer" une fonction complexe
Regardez à nouveau la fonction précédente. Pouvez-vous comprendre la séquence « emballage » ? Dans quoi X a été inséré en premier, dans quoi ensuite, et ainsi de suite jusqu'à la toute fin. Autrement dit, quelle fonction est imbriquée dans laquelle ? Prenez une feuille de papier et écrivez ce que vous pensez. Vous pouvez le faire avec une chaîne avec des flèches comme nous l'avons écrit ci-dessus ou de toute autre manière.
Maintenant, la bonne réponse est : d’abord, x a été « compressé » dans la \(4\)ième puissance, puis le résultat a été compressé dans un sinus, celui-ci, à son tour, a été placé dans le logarithme à la base \(2\) , et à la fin toute cette construction a été mise dans une puissance cinq.
Autrement dit, vous devez dérouler la séquence DANS L'ORDRE INVERSE. Et voici un indice pour y parvenir plus facilement : regardez immédiatement le X – vous devriez danser dessus. Regardons quelques exemples.
Par exemple, voici la fonction suivante : \(y=tg(\log_2x)\). Nous regardons X - que lui arrive-t-il en premier ? Pris de lui. Et puis? La tangente du résultat est prise. La séquence sera la même :
\(x → \log_2x → tg(\log_2x)\)
Autre exemple : \(y=\cos((x^3))\). Analysons - nous avons d'abord divisé X au cube, puis avons pris le cosinus du résultat. Cela signifie que la séquence sera : \(x → x^3 → \cos((x^3))\). Attention, la fonction semble être similaire à la toute première (où elle a des images). Mais c'est une fonction complètement différente : ici dans le cube se trouve x (c'est-à-dire \(\cos((x·x·x)))\), et là dans le cube se trouve le cosinus \(x\) ( c'est-à-dire \(\cos x·\cosx·\cosx\)). Cette différence provient de différentes séquences de « packing ».
Le dernier exemple (avec une information important dedans): \(y=\sin((2x+5))\). Il est clair qu'ici ils ont d'abord fait des opérations arithmétiques avec x, puis ont pris le sinus du résultat : \(x → 2x+5 → \sin((2x+5))\). Et ça point important: malgré le fait que les opérations arithmétiques ne sont pas des fonctions en elles-mêmes, elles agissent ici aussi comme un moyen de « packaging ». Approfondissons un peu cette subtilité.
Comme je l'ai dit plus haut, dans les fonctions simples, x est « compressé » une fois, et dans les fonctions complexes, deux ou plus. De plus, toute combinaison de fonctions simples (c'est-à-dire leur somme, leur différence, leur multiplication ou leur division) est également fonction simple. Par exemple, \(x^7\) est une fonction simple, tout comme \(ctg x\). Cela signifie que toutes leurs combinaisons sont des fonctions simples :
\(x^7+ ctg x\) - simple,
\(x^7· lit bébé x\) – simple,
\(\frac(x^7)(ctg x)\) – simple, etc.
Cependant, si une fonction supplémentaire est appliquée à une telle combinaison, elle deviendra une fonction complexe, puisqu'il y aura deux « packages ». Voir schéma :

OK, vas-y maintenant. Écrivez la séquence de fonctions de « wrapping » :
\(y=cos((sinx))\)
\(y=5^(x^7)\)
\(y=arctg(11^x)\)
\(y=log_2(1+x)\)
Les réponses se trouvent à nouveau à la fin de l'article.
Fonctions internes et externes
Pourquoi devons-nous comprendre l’imbrication des fonctions ? Qu'est-ce que cela nous donne ? Le fait est que sans une telle analyse, nous ne pourrons pas trouver de manière fiable les dérivées des fonctions évoquées ci-dessus.
Et pour avancer, nous aurons besoin de deux autres concepts : les fonctions internes et externes. C'est très Chose simple, d'ailleurs, en fait, nous les avons déjà analysés plus haut : si l'on rappelle notre analogie du tout début, alors la fonction interne est un « package », et la fonction externe est une « boîte ». Ceux. ce dans quoi X est « enveloppé » en premier est une fonction interne, et ce dans quoi la fonction interne est « enveloppée » est déjà externe. Eh bien, c'est clair pourquoi - elle est dehors, cela veut dire externe.
Dans cet exemple : \(y=tg(log_2x)\), la fonction \(\log_2x\) est interne, et  - externe.
- externe.
Et en ceci : \(y=\cos((x^3+2x+1))\), \(x^3+2x+1\) est interne, et  - externe.
- externe.
Terminez la dernière pratique d'analyse de fonctions complexes, et passons enfin à ce pour quoi nous avons tous commencé - nous trouverons les dérivées de fonctions complexes :
Remplissez les espaces vides du tableau :
Dérivée d'une fonction complexe
Bravo à nous, nous sommes enfin arrivés au « patron » de ce sujet - en fait, un dérivé fonction complexe, et plus précisément, à cette formule très terrible du début de l'article.☺
\((f(g(x)))"=f"(g(x))\cdot g"(x)\)
Cette formule se lit ainsi :
La dérivée d'une fonction complexe est égale au produit de la dérivée de la fonction externe par rapport à une fonction interne constante et de la dérivée de la fonction interne.
Et regardez immédiatement le diagramme d'analyse, selon les mots, pour comprendre quoi faire avec quoi :

J'espère que les termes « dérivé » et « produit » ne posent aucune difficulté. "Fonction complexe" - nous l'avons déjà réglé. Le problème réside dans la « dérivée d’une fonction externe par rapport à une fonction interne constante ». Ce que c'est?
Réponse : il s'agit de la dérivée habituelle d'une fonction externe, dans laquelle seule la fonction externe change et la fonction interne reste la même. Ce n'est toujours pas clair ? D'accord, utilisons un exemple.
Ayons une fonction \(y=\sin(x^3)\). Il est clair que la fonction interne est ici \(x^3\), et la fonction externe  . Trouvons maintenant la dérivée de l'extérieur par rapport à l'intérieur constant.
. Trouvons maintenant la dérivée de l'extérieur par rapport à l'intérieur constant.
Après une préparation préliminaire de l'artillerie, les exemples avec des imbrications de fonctions 3-4-5 seront moins effrayants. Peut-être que les deux exemples suivants sembleront compliqués à certains, mais si vous les comprenez (quelqu'un en souffrira), alors presque tout le reste est calculs différentiels Cela ressemblera à une blague d'enfant.
Exemple 2
Trouver la dérivée d'une fonction
Comme déjà noté, pour trouver la dérivée d'une fonction complexe, il faut tout d'abord Droite COMPRENEZ vos investissements. En cas de doute, je vous rappelle astuce utile: nous prenons par exemple le sens expérimental de « x » et essayons (mentalement ou dans un brouillon) de substituer ce sens dans « l'expression terrible ».
1) Nous devons d’abord calculer l’expression, ce qui signifie que la somme est l’intégration la plus profonde.
2) Ensuite, vous devez calculer le logarithme :
4) Puis cubez le cosinus :
5) A la cinquième étape la différence :
6) Et enfin, la fonction la plus externe est la racine carrée : ![]()
Formule pour différencier une fonction complexe ![]() sont appliqués dans l’ordre inverse, de la fonction la plus externe à la fonction la plus interne. Nous décidons:
sont appliqués dans l’ordre inverse, de la fonction la plus externe à la fonction la plus interne. Nous décidons:

Il ne semble y avoir aucune erreur :
1) Prenez la dérivée de la racine carrée.
2) Prendre la dérivée de la différence en utilisant la règle ![]()
3) La dérivée d'un triplet est nulle. Au deuxième terme on prend la dérivée du degré (cube).
4) Prenez la dérivée du cosinus.
6) Et enfin, on prend la dérivée du plongement le plus profond.
Cela peut paraître trop difficile, mais ce n’est pas l’exemple le plus brutal. Prenez, par exemple, la collection de Kuznetsov et vous apprécierez toute la beauté et la simplicité du dérivé analysé. J'ai remarqué qu'ils aiment donner une chose similaire lors d'un examen pour vérifier si un étudiant comprend comment trouver la dérivée d'une fonction complexe ou ne comprend pas.
L'exemple suivant est pour décision indépendante.
Exemple 3
Trouver la dérivée d'une fonction
Astuce : nous appliquons d’abord les règles de linéarité et la règle de différenciation des produits.
Solution complète et réponse à la fin de la leçon.
Il est temps de passer à quelque chose de plus petit et de plus joli.
Il n'est pas rare qu'un exemple montre le produit non pas de deux, mais trois fonctions. Comment trouver la dérivée du produit de trois facteurs ?
Exemple 4
Trouver la dérivée d'une fonction ![]()
Tout d’abord, regardons : est-il possible de transformer le produit de trois fonctions en produit de deux fonctions ? Par exemple, si nous avions deux polynômes dans le produit, nous pourrions alors ouvrir les parenthèses. Mais dans l’exemple considéré, toutes les fonctions sont différentes : degré, exposant et logarithme.
Dans de tels cas, il est nécessaire séquentiellement appliquer la règle de différenciation des produits ![]() deux fois
deux fois
L'astuce est que par « y » nous désignons le produit de deux fonctions : , et par « ve » nous désignons le logarithme : . Pourquoi cela peut-il être fait ? Est ce que c'est vraiment ![]() - ce n'est pas le produit de deux facteurs et la règle ne fonctionne pas ?! Il n'y a rien de compliqué :
- ce n'est pas le produit de deux facteurs et la règle ne fonctionne pas ?! Il n'y a rien de compliqué :
Reste maintenant à appliquer la règle une seconde fois ![]() mettre entre parenthèses :
mettre entre parenthèses :
Vous pouvez toujours être pervers et prendre quelque chose entre parenthèses, mais dans dans ce cas Il est préférable de laisser la réponse sous cette forme - ce sera plus facile à vérifier.
L'exemple considéré peut être résolu de la deuxième manière :

Les deux solutions sont absolument équivalentes.
Exemple 5
Trouver la dérivée d'une fonction
Ceci est un exemple de solution indépendante ; dans l’exemple, elle est résolue en utilisant la première méthode.
Regardons des exemples similaires avec des fractions.
Exemple 6
Trouver la dérivée d'une fonction ![]()
Vous pouvez y accéder de plusieurs manières :
Ou comme ceci :
Mais la solution s'écrira de manière plus compacte si l'on utilise d'abord la règle de différenciation du quotient  , en prenant pour tout le numérateur :
, en prenant pour tout le numérateur :

En principe, l’exemple est résolu, et s’il reste tel quel, ce ne sera pas une erreur. Mais si vous avez le temps, il est toujours conseillé de vérifier sur un brouillon pour voir si la réponse peut être simplifiée ?
Réduisons l'expression du numérateur à dénominateur commun et débarrassons-nous de la fraction à trois étages:

L'inconvénient des simplifications supplémentaires est qu'il y a un risque de se tromper non pas lors de la recherche de la dérivée, mais lors de transformations scolaires banales. D'un autre côté, les enseignants rejettent souvent le devoir et demandent de « y penser » par la dérivée.
Un exemple plus simple à résoudre par vous-même :
Exemple 7
Trouver la dérivée d'une fonction
Nous continuons à maîtriser les méthodes de recherche de la dérivée, et nous allons maintenant considérer un cas typique où le logarithme « terrible » est proposé pour la différenciation
Résoudre des problèmes physiques ou des exemples mathématiques est totalement impossible sans la connaissance de la dérivée et des méthodes de calcul. La dérivée est l'un des concepts les plus importants analyse mathematique. Nous avons décidé de consacrer l’article d’aujourd’hui à ce sujet fondamental. Qu'est-ce qu'un dérivé, quelle est sa nature physique et signification géométrique comment calculer la dérivée d'une fonction ? Toutes ces questions peuvent être regroupées en une seule : comment comprendre la dérivée ?
Signification géométrique et physique de la dérivée
Qu'il y ait une fonction f(x) , spécifié dans un certain intervalle (un B) . Les points x et x0 appartiennent à cet intervalle. Lorsque x change, la fonction elle-même change. Changer l'argument - la différence de ses valeurs x-x0 . Cette différence s’écrit deltax et est appelé incrément d’argument. Un changement ou un incrément d'une fonction est la différence entre les valeurs d'une fonction en deux points. Définition du dérivé :
La dérivée d'une fonction en un point est la limite du rapport de l'incrément de la fonction en un point donné à l'incrément de l'argument lorsque ce dernier tend vers zéro.
Sinon, cela peut s'écrire ainsi :

Quel est l'intérêt de trouver une telle limite ? Et voici ce que c'est :
la dérivée d'une fonction en un point est égale à la tangente de l'angle entre l'axe OX et la tangente au graphique de la fonction en un point donné.

Signification physique de la dérivée : la dérivée de la trajectoire par rapport au temps est égale à la vitesse du mouvement rectiligne.
En effet, depuis l'école tout le monde sait que la vitesse est un chemin particulier x=f(t) et le temps t . vitesse moyenne pendant une certaine période :

Pour connaître la vitesse de déplacement à un instant donné t0 vous devez calculer la limite :

Première règle : définir une constante
La constante peut être soustraite du signe dérivé. De plus, cela doit être fait. Lorsque vous résolvez des exemples en mathématiques, prenez-le comme règle : Si vous pouvez simplifier une expression, assurez-vous de la simplifier .
Exemple. Calculons la dérivée :

Deuxième règle : dérivée de la somme des fonctions
La dérivée de la somme de deux fonctions est égale à la somme des dérivées de ces fonctions. Il en va de même pour la dérivée de la différence de fonctions.

Nous ne donnerons pas de démonstration de ce théorème, mais considérerons plutôt un exemple pratique.
Trouvez la dérivée de la fonction :


Troisième règle : dérivée du produit de fonctions
La dérivée du produit de deux fonctions différentiables est calculée par la formule :

Exemple : trouver la dérivée d'une fonction :

Solution: 
Il est important de parler ici du calcul des dérivées de fonctions complexes. La dérivée d'une fonction complexe est égale au produit de la dérivée de cette fonction par rapport à l'argument intermédiaire et de la dérivée de l'argument intermédiaire par rapport à la variable indépendante.
DANS exemple ci-dessus on retrouve l'expression :

Dans ce cas, l’argument intermédiaire est 8x à la puissance cinq. Afin de calculer la dérivée d'une telle expression, nous calculons d'abord la dérivée de la fonction externe par rapport à l'argument intermédiaire, puis multiplions par la dérivée de l'argument intermédiaire lui-même par rapport à la variable indépendante.
Règle quatre : dérivée du quotient de deux fonctions
Formule pour déterminer la dérivée du quotient de deux fonctions :



Nous avons essayé de parler de produits dérivés pour les nuls à partir de zéro. Ce sujet n'est pas aussi simple qu'il y paraît, alors soyez prévenu : il y a souvent des pièges dans les exemples, alors soyez prudent lors du calcul des dérivées.
Pour toute question sur ce sujet ou sur d’autres sujets, vous pouvez contacter le service étudiants. Derrière court terme Nous vous aiderons à résoudre les tests les plus difficiles et à résoudre les problèmes, même si vous n'avez jamais effectué de calculs de dérivées auparavant.
Les fonctions type complexe ne correspondent pas toujours à la définition d’une fonction complexe. S'il existe une fonction de la forme y = sin x - (2 - 3) · a r c t g x x 5 7 x 10 - 17 x 3 + x - 11, alors elle ne peut pas être considérée comme complexe, contrairement à y = sin 2 x.
Cet article montrera le concept de fonction complexe et son identification. Travaillons avec des formules pour trouver la dérivée avec des exemples de solutions en conclusion. L'utilisation de la table de dérivées et des règles de différenciation réduit considérablement le temps nécessaire pour trouver la dérivée.
Yandex.RTB R-A-339285-1
Définitions basiques
Définition 1Une fonction complexe est une fonction dont l’argument est aussi une fonction.
Il est noté ainsi : f (g (x)). Nous avons que la fonction g (x) est considérée comme un argument f (g (x)).
Définition 2
S'il existe une fonction f et qu'elle est une fonction cotangente, alors g(x) = ln x est la fonction logarithme népérien. Nous constatons que la fonction complexe f (g (x)) s’écrira arctg(lnx). Soit une fonction f, qui est une fonction élevée à la puissance 4, où g (x) = x 2 + 2 x - 3 est considérée comme une fonction rationnelle entière, on obtient que f (g (x)) = (x 2 + 2x-3) 4 .
Évidemment, g(x) peut être complexe. D'après l'exemple y = sin 2 x + 1 x 3 - 5, il est clair que la valeur de g est racine cubique avec une fraction. Cette expression peut être notée y = f (f 1 (f 2 (x))). D'où on a que f est une fonction sinusoïdale, et f 1 est une fonction située sous racine carrée, f 2 (x) = 2 x + 1 x 3 - 5 - fonction rationnelle fractionnaire.
Définition 3
Le degré d'imbrication est déterminé par tout entier naturel et s'écrit y = f (f 1 (f 2 (f 3 (... (f n (x)))))) .
Définition 4
Le concept de composition de fonctions fait référence au nombre de fonctions imbriquées selon les conditions du problème. Pour résoudre, utilisez la formule pour trouver la dérivée d'une fonction complexe de la forme
(f (g (x))) " = f " (g (x)) g " (x)
Exemples
Exemple 1Trouver la dérivée d'une fonction complexe de la forme y = (2 x + 1) 2.
Solution
La condition montre que f est une fonction quadratique et que g(x) = 2 x + 1 est considéré comme une fonction linéaire.
Appliquons la formule dérivée pour une fonction complexe et écrivons :
f " (g (x)) = ((g (x)) 2) " = 2 (g (x)) 2 - 1 = 2 g (x) = 2 (2 x + 1) ; g " (x) = (2 x + 1) " = (2 x) " + 1 " = 2 x " + 0 = 2 1 x 1 - 1 = 2 ⇒ (f (g (x))) " = f " (g (x)) g " (x) = 2 (2 x + 1) 2 = 8 x + 4
Il faut trouver la dérivée avec une forme originale simplifiée de la fonction. On a:
y = (2 x + 1) 2 = 4 x 2 + 4 x + 1
De là, nous avons ça
y " = (4 x 2 + 4 x + 1) " = (4 x 2) " + (4 x) " + 1 " = 4 (x 2) " + 4 (x) " + 0 = = 4 · 2 · x 2 - 1 + 4 · 1 · x 1 - 1 = 8 x + 4
Les résultats étaient les mêmes.
Lors de la résolution de problèmes de ce type, il est important de comprendre où se situera la fonction de forme f et g (x).
Exemple 2
Vous devriez trouver les dérivées de fonctions complexes de la forme y = sin 2 x et y = sin x 2.
Solution
La première notation de fonction dit que f est la fonction de quadrature et g(x) est la fonction sinusoïdale. Ensuite, nous obtenons cela
y " = (sin 2 x) " = 2 sin 2 - 1 x (sin x) " = 2 sin x cos x
La deuxième entrée montre que f est une fonction sinusoïdale et que g(x) = x 2 est noté fonction de puissance. Il s’ensuit que nous écrivons le produit d’une fonction complexe sous la forme
y " = (sin x 2) " = cos (x 2) (x 2) " = cos (x 2) 2 x 2 - 1 = 2 x cos (x 2)
La formule de la dérivée y = f (f 1 (f 2 (f 3 (. . . (f n (x))))) s'écrira y " = f " (f 1 (f 2 (f 3 (. . ( f n (x)))) · f 1 " (f 2 (f 3 (. . . (f n (x)))) · · f 2 " (f 3 (. . . (f n (x) )) )) · . . . fn "(x)
Exemple 3
Trouvez la dérivée de la fonction y = sin (ln 3 a r c t g (2 x)).
Solution
Cet exemple montre la difficulté d’écrire et de déterminer l’emplacement des fonctions. Alors y = f (f 1 (f 2 (f 3 (f 4 (x))))) désigne où f , f 1 , f 2 , f 3 , f 4 (x) est la fonction sinusoïdale, la fonction d'augmentation à 3 degrés, fonction avec logarithme et base e, fonction arctangente et linéaire.
De la formule pour définir une fonction complexe, nous avons cela
y " = f " (f 1 (f 2 (f 3 (f 4 (x)))) f 1 " (f 2 (f 3 (f 4 (x)))) f 2 " (f 3 (f 4 (x)) f 3 " (f 4 (x)) f 4 " (x)
Nous obtenons ce dont nous avons besoin pour trouver
- f " (f 1 (f 2 (f 3 (f 4 (x))))) comme dérivée du sinus selon le tableau des dérivées, puis f " (f 1 (f 2 (f 3 (f 4 ( x)))) ) = cos (ln 3 a r c t g (2 x)) .
- f 1 " (f 2 (f 3 (f 4 (x)))) comme dérivée d'une fonction puissance, alors f 1 " (f 2 (f 3 (f 4 (x)))) = 3 ln 3 - 1 a r c t g (2 x) = 3 ln 2 a r c t g (2 x) .
- f 2 " (f 3 (f 4 (x))) comme dérivée logarithmique, alors f 2 " (f 3 (f 4 (x))) = 1 a r c t g (2 x) .
- f 3 " (f 4 (x)) comme dérivée de l'arctangente, alors f 3 " (f 4 (x)) = 1 1 + (2 x) 2 = 1 1 + 4 x 2.
- Lors de la recherche de la dérivée f 4 (x) = 2 x, supprimez 2 du signe de la dérivée en utilisant la formule de la dérivée d'une fonction puissance avec un exposant égal à 1, alors f 4 " (x) = (2 x) " = 2 x " = 2 · 1 · x 1 - 1 = 2 .
Nous combinons les résultats intermédiaires et obtenons cela
y " = f " (f 1 (f 2 (f 3 (f 4 (x)))) f 1 " (f 2 (f 3 (f 4 (x)))) f 2 " (f 3 (f 4 (x)) f 3 " (f 4 (x)) f 4 " (x) = = cos (ln 3 a r c t g (2 x)) 3 ln 2 a r c t g (2 x) 1 a r c t g (2 x) 1 1 + 4 x 2 2 = = 6 cos (ln 3 a r c t g (2 x)) ln 2 a r c t g (2 x) a r c t g (2 x) (1 + 4 x 2)
L’analyse de telles fonctions n’est pas sans rappeler celle des poupées gigognes. Les règles de différenciation ne peuvent pas toujours être appliquées explicitement à l'aide d'une table dérivée. Vous devez souvent utiliser une formule pour trouver des dérivées de fonctions complexes.
Il existe certaines différences entre l'apparence complexe et les fonctions complexes. Avec une capacité claire à distinguer cela, trouver des dérivés sera particulièrement facile.
Exemple 4
Il faut envisager de donner un tel exemple. S'il existe une fonction de la forme y = t g 2 x + 3 t g x + 1, alors elle peut être considérée comme une fonction complexe de la forme g (x) = t g x, f (g) = g 2 + 3 g + 1 . Évidemment, il faut utiliser la formule d'une dérivée complexe :
f " (g (x)) = (g 2 (x) + 3 g (x) + 1) " = (g 2 (x)) " + (3 g (x)) " + 1 " = = 2 · g 2 - 1 (x) + 3 g " (x) + 0 = 2 g (x) + 3 1 g 1 - 1 (x) = = 2 g (x) + 3 = 2 t g x + 3 ; g " (x) = (t g x) " = 1 cos 2 x ⇒ y " = (f (g (x))) " = f " (g (x)) g " (x) = (2 t g x + 3 ) · 1 cos 2 x = 2 t g x + 3 cos 2 x
Une fonction de la forme y = t g x 2 + 3 t g x + 1 n'est pas considérée comme complexe, car elle a la somme de t g x 2, 3 t g x et 1. Cependant, t g x 2 est considéré comme une fonction complexe, on obtient alors une fonction puissance de la forme g (x) = x 2 et f, qui est une fonction tangente. Pour ce faire, différenciez par montant. Nous obtenons cela
y " = (t g x 2 + 3 t g x + 1) " = (t g x 2) " + (3 t g x) " + 1 " = = (t g x 2) " + 3 (t g x) " + 0 = (t g x 2) " + 3 parce que 2 x
Passons à la recherche de la dérivée d'une fonction complexe (t g x 2) » :
f " (g (x)) = (t g (g (x))) " = 1 cos 2 g (x) = 1 cos 2 (x 2) g " (x) = (x 2) " = 2 x 2 - 1 = 2 x ⇒ (t g x 2) " = f " (g (x)) g " (x) = 2 x cos 2 (x 2)
On obtient que y " = (t g x 2 + 3 t g x + 1) " = (t g x 2) " + 3 cos 2 x = 2 x cos 2 (x 2) + 3 cos 2 x
Les fonctions d'un type complexe peuvent être incluses dans des fonctions complexes, et les fonctions complexes elles-mêmes peuvent être des composants de fonctions d'un type complexe.
Exemple 5
Par exemple, considérons une fonction complexe de la forme y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 + ln 2 x (x 2 + 1)
Cette fonction peut être représentée par y = f (g (x)), où la valeur de f est fonction du logarithme en base 3, et g (x) est considéré comme la somme de deux fonctions de la forme h (x) = x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 et k (x) = ln 2 x (x 2 + 1) . Évidemment, y = f (h (x) + k (x)).
Considérons la fonction h(x). C'est le rapport l (x) = x 2 + 3 cos 3 (2 x + 1) + 7 à m (x) = e x 2 + 3 3
On a que l (x) = x 2 + 3 cos 2 (2 x + 1) + 7 = n (x) + p (x) est la somme de deux fonctions n (x) = x 2 + 7 et p ( x) = 3 cos 3 (2 x + 1) , où p (x) = 3 p 1 (p 2 (p 3 (x))) est une fonction complexe avec un coefficient numérique 3, et p 1 est une fonction cubique, p 2 par une fonction cosinus, p 3 (x) = 2 x + 1 par une fonction linéaire.
Nous avons constaté que m (x) = e x 2 + 3 3 = q (x) + r (x) est la somme de deux fonctions q (x) = e x 2 et r (x) = 3 3, où q (x) = q 1 (q 2 (x)) est une fonction complexe, q 1 est une fonction avec une exponentielle, q 2 (x) = x 2 est une fonction puissance.
Cela montre que h (x) = l (x) m (x) = n (x) + p (x) q (x) + r (x) = n (x) + 3 p 1 (p 2 ( p 3 (x))) q 1 (q 2 (x)) + r (x)
Lorsqu'on passe à une expression de la forme k (x) = ln 2 x · (x 2 + 1) = s (x) · t (x), il est clair que la fonction se présente sous la forme d'un complexe s ( x) = ln 2 x = s 1 ( s 2 (x)) avec un entier rationnel t (x) = x 2 + 1, où s 1 est une fonction quadratique, et s 2 (x) = ln x est logarithmique avec base e.
Il s'ensuit que l'expression prendra la forme k (x) = s (x) · t (x) = s 1 (s 2 (x)) · t (x).
Ensuite, nous obtenons cela
y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 + ln 2 x (x 2 + 1) = = f n (x) + 3 p 1 (p 2 (p 3 ( x))) q 1 (q 2 (x)) = r (x) + s 1 (s 2 (x)) t (x)
Sur la base des structures de la fonction, il est devenu clair comment et quelles formules doivent être utilisées pour simplifier l'expression lors de sa différenciation. Pour se familiariser avec de tels problèmes et le concept de leur solution, il faut se tourner vers la différenciation d'une fonction, c'est-à-dire trouver sa dérivée.
Si vous remarquez une erreur dans le texte, veuillez la surligner et appuyer sur Ctrl+Entrée




