Fractionnement rationnel. Résolution d'équations entières et fractionnellement rationnelles
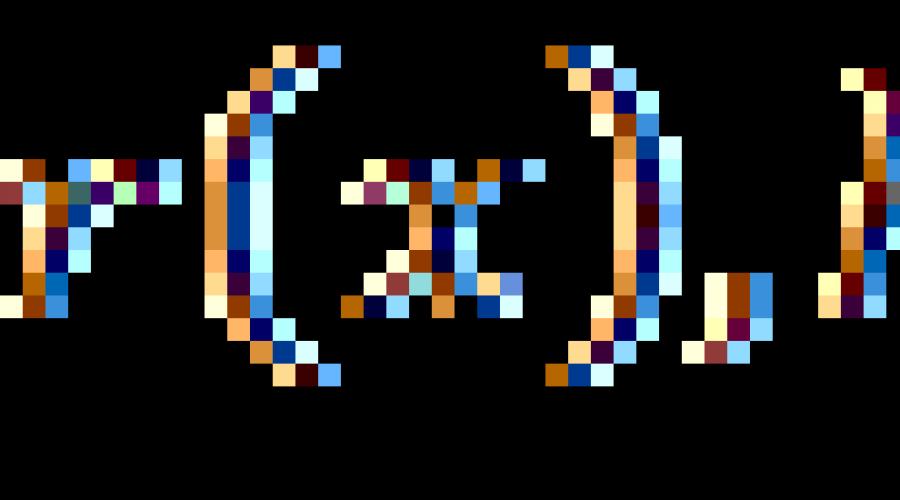
Lire aussi
« Équations rationnelles avec des polynômes" est l'un des sujets les plus courants dans les tests UTILISER les devoirs mathématiques. Pour cette raison, leur répétition doit être donnée Attention particulière. De nombreux élèves sont confrontés au problème de trouver le discriminant, de transférer les indicateurs du côté droit au côté gauche et de ramener l'équation à un dénominateur commun, ce qui rend difficile la réalisation de telles tâches. Résoudre des équations rationnelles en préparation de l'examen sur notre site Web vous aidera à faire face rapidement à des tâches de toute complexité et à réussir parfaitement le test.
Choisissez le portail éducatif "Shkolkovo" pour une préparation réussie à l'examen unifié de mathématiques !
Connaître les règles de calcul des inconnues et obtenir facilement résultats corrects utiliser notre service en ligne. Le portail "Shkolkovo" est une plate-forme unique en son genre où le nécessaire UTILISER des matériaux. Nos professeurs ont systématisé et présenté sous une forme compréhensible toutes les règles mathématiques. De plus, nous invitons les écoliers à s'essayer à la résolution d'équations rationnelles typiques, dont la base est constamment mise à jour et complétée.
Pour une préparation plus efficace aux tests, nous vous recommandons de suivre nos méthode spéciale et commencez par répéter les règles et résolvez tâches simples, passant progressivement à des plus complexes. Ainsi, le diplômé pourra mettre en évidence les sujets les plus difficiles pour lui-même et se concentrer sur leur étude.
Commencez dès aujourd'hui à vous préparer pour les tests finaux avec Shkolkovo, et le résultat ne vous fera pas attendre ! Choisissez l'exemple le plus simple parmi ceux donnés. Si vous avez rapidement maîtrisé l'expression, passez à plus tâche difficile. Ainsi, vous pouvez améliorer vos connaissances jusqu'à résoudre des tâches USE en mathématiques au niveau du profil.
L'éducation est accessible non seulement aux diplômés de Moscou, mais également aux écoliers d'autres villes. Passez quelques heures par jour à étudier sur notre portail, par exemple, et très bientôt vous pourrez faire face à des équations de n'importe quelle complexité !
Nous avons déjà appris à résoudre des équations quadratiques. Étendons maintenant les méthodes étudiées aux équations rationnelles.
Qu'est-ce qu'une expression rationnelle ? Nous avons déjà rencontré ce concept. Expressions rationnelles appelées expressions composées de nombres, de variables, de leurs degrés et signes d'opérations mathématiques.
Par conséquent, les équations rationnelles sont des équations de la forme : , où ![]() - expressions rationnelles.
- expressions rationnelles.
Auparavant, nous ne considérions que les équations rationnelles qui se réduisent à des équations linéaires. Considérons maintenant ces équations rationnelles qui peuvent être réduites à des équations quadratiques.
Exemple 1
Résous l'équation: .
Décision:
![]()
![]()
![]()
![]()
Une fraction vaut 0 si et seulement si son numérateur est 0 et son dénominateur différent de 0.
On obtient le système suivant :
![]()
La première équation du système est équation quadratique. Avant de le résoudre, on divise tous ses coefficients par 3. On obtient :
![]()
On obtient deux racines : ; .
Comme 2 n'est jamais égal à 0, deux conditions doivent être remplies : ![]() . Puisqu'aucune des racines d'équation obtenues ci-dessus ne correspond aux valeurs invalides de la variable résultant de la résolution de la deuxième inégalité, elles sont toutes deux des solutions équation donnée.
. Puisqu'aucune des racines d'équation obtenues ci-dessus ne correspond aux valeurs invalides de la variable résultant de la résolution de la deuxième inégalité, elles sont toutes deux des solutions équation donnée.
Réponse:.
Alors, formulons un algorithme pour résoudre des équations rationnelles :
1. Transférer tous les termes à côté gauche pour obtenir 0 sur le côté droit.
2. Transformez et simplifiez le côté gauche, amenez toutes les fractions à un dénominateur commun.
3. Égalez la fraction résultante à 0, selon l'algorithme suivant : ![]() .
.
4. Notez les racines qui sont obtenues dans la première équation et satisfont la deuxième inégalité en réponse.
Prenons un autre exemple.
Exemple 2
Résous l'équation: ![]() .
.
Décision
Au tout début, on reporte tous les termes à gauche pour que 0 reste à droite. On obtient :
![]()
Maintenant, amenons le côté gauche de l'équation à un dénominateur commun :
![]()
![]()
![]()
![]()
![]()
Cette équation est équivalente au système :
![]()
La première équation du système est une équation quadratique.
Les coefficients de cette équation : . On calcule le discriminant :
On obtient deux racines : ; .
Résolvons maintenant la seconde inégalité : le produit des facteurs n'est pas égal à 0 si et seulement si aucun des facteurs n'est égal à 0.
Deux conditions doivent être remplies : ![]() . On obtient que des deux racines de la première équation, une seule convient - 3.
. On obtient que des deux racines de la première équation, une seule convient - 3.
Réponse:.
Dans cette leçon, nous avons rappelé ce qu'est une expression rationnelle, et avons également appris à résoudre des équations rationnelles, qui sont réduites à des équations quadratiques.
Dans la prochaine leçon, nous considérerons les équations rationnelles comme des modèles de situations réelles, ainsi que des problèmes de mouvement.
Bibliographie
- Bashmakov M.I. Algèbre, 8e année. - M. : Lumières, 2004.
- Dorofeev G.V., Suvorova S.B., Bunimovich E.A. et autres Algèbre, 8. 5e éd. - M. : Éducation, 2010.
- Nikolsky S.M., Potapov M.A., Reshetnikov N.N., Shevkin A.V. Algèbre, 8e année. Tutoriel pour les établissements d'enseignement. - M. : Éducation, 2006.
- Festival idées pédagogiques "Leçon publique" ().
- School.xvatit.com().
- Rudocs.exdat.com().
§ 1 Équations rationnelles entières et fractionnaires
Dans cette leçon, nous analyserons des concepts tels qu'une équation rationnelle, une expression rationnelle, une expression entière, une expression fractionnaire. Considérons la solution d'équations rationnelles.
Une équation rationnelle est une équation dans laquelle les membres gauche et droit sont des expressions rationnelles.
Les expressions rationnelles sont :
Fractionnaire.
Une expression entière est composée de nombres, de variables, de puissances entières utilisant les opérations d'addition, de soustraction, de multiplication et de division par un nombre autre que zéro.
Par example:
Dans les expressions fractionnaires, il y a une division par une variable ou une expression avec une variable. Par example:
Une expression fractionnaire n'a pas de sens pour toutes les valeurs des variables qui y sont incluses. Par exemple, l'expression
à x = -9, cela n'a pas de sens, car à x = -9, le dénominateur tend vers zéro.
Cela signifie qu'une équation rationnelle peut être entière et fractionnaire.
Une équation rationnelle entière est une équation rationnelle dans laquelle les côtés gauche et droit sont des expressions entières.
Par example:
![]()
Une équation rationnelle fractionnaire est une équation rationnelle dans laquelle les côtés gauche ou droit sont des expressions fractionnaires.
Par example:

§ 2 Solution d'une équation rationnelle entière
Considérons la solution d'une équation rationnelle entière.
Par example:
Multiplier les deux membres de l'équation par le plus petit dénominateur commun dénominateurs de ses fractions.
Pour ça:
1. trouver un dénominateur commun pour les dénominateurs 2, 3, 6. Il est égal à 6 ;
2. trouver un facteur supplémentaire pour chaque fraction. Pour ce faire, divisez le dénominateur commun 6 par chaque dénominateur
multiplicateur supplémentaire pour la fraction
multiplicateur supplémentaire pour la fraction
3. multiplier les numérateurs des fractions par les facteurs supplémentaires qui leur correspondent. Ainsi, on obtient l'équation
![]()
ce qui équivaut à cette équation
Ouvrons les parenthèses à gauche, déplaçons la partie droite vers la gauche, en changeant le signe du terme lors du transfert vers le contraire.
![]()
Nous donnons des termes similaires du polynôme et obtenons
On voit que l'équation est linéaire.
En le résolvant, nous trouvons que x = 0,5.
§ 3 Solution d'une équation rationnelle fractionnaire
Considérons la solution d'une équation rationnelle fractionnaire.
Par example:
![]()
1. Multipliez les deux côtés de l'équation par le plus petit dénominateur commun des dénominateurs des fractions rationnelles qui y sont incluses.
Trouvez le dénominateur commun des dénominateurs x + 7 et x - 1.
Il est égal à leur produit (x + 7)(x - 1).
2. Trouvons un facteur supplémentaire pour chaque fraction rationnelle.
Pour ce faire, nous divisons le dénominateur commun (x + 7) (x - 1) par chaque dénominateur. Multiplicateur supplémentaire pour les fractions
est égal à x - 1,
multiplicateur supplémentaire pour la fraction
est égal à x+7.
3. Multipliez les numérateurs des fractions par leurs facteurs supplémentaires correspondants.
Nous obtenons l'équation (2x - 1) (x - 1) \u003d (3x + 4) (x + 7), qui équivaut à cette équation
4.Gauche et droite multiplient le binôme par le binôme et obtiennent l'équation suivante
5. Nous transférons la partie droite vers la gauche, en changeant le signe de chaque terme lors du transfert vers l'opposé:
6. Nous présentons des membres similaires du polynôme :
![]()
7. Vous pouvez diviser les deux parties par -1. On obtient une équation quadratique :
![]()
8. Après l'avoir résolu, nous trouverons les racines
![]()
Puisque dans l'équation
les parties gauche et droite sont des expressions fractionnaires, et dans les expressions fractionnaires, pour certaines valeurs des variables, le dénominateur peut s'annuler, il faut alors vérifier si le dénominateur commun ne s'annule pas lorsque x1 et x2 sont trouvés.
A x = -27 le dénominateur commun (x + 7)(x - 1) ne s'annule pas, à x = -1 le dénominateur commun est également non nul.
Par conséquent, les racines -27 et -1 sont les racines de l'équation.
Lors de la résolution d'une équation rationnelle fractionnaire, il est préférable d'indiquer immédiatement l'aire valeurs autorisées. Éliminez les valeurs auxquelles le dénominateur commun va à zéro.
Prenons un autre exemple de résolution d'une équation rationnelle fractionnaire.
Par exemple, résolvons l'équation
![]()
Nous décomposons le dénominateur de la fraction du côté droit de l'équation en facteurs
![]()
On obtient l'équation

Trouvez un dénominateur commun pour les dénominateurs (x - 5), x, x (x - 5).
Ce sera l'expression x (x - 5).
maintenant, trouvons la plage des valeurs admissibles de l'équation
Pour ce faire, nous assimilons le dénominateur commun à zéro x (x - 5) \u003d 0.
Nous obtenons une équation, en résolvant laquelle, nous constatons qu'à x \u003d 0 ou à x \u003d 5, le dénominateur commun disparaît.
Donc x = 0 ou x = 5 ne peuvent pas être les racines de notre équation.
Vous pouvez maintenant trouver des multiplicateurs supplémentaires.
Multiplicateur supplémentaire pour les fractions rationnelles
multiplicateur supplémentaire pour les fractions
sera (x - 5),
et le facteur supplémentaire de la fraction
Nous multiplions les numérateurs par les facteurs supplémentaires correspondants.
Nous obtenons l'équation x(x - 3) + 1(x - 5) = 1(x + 5).
Ouvrons les parenthèses à gauche et à droite, x2 - 3x + x - 5 = x + 5.
Déplaçons les termes de droite à gauche en changeant le signe des termes à déplacer :
X2 - 3x + x - 5 - x - 5 = 0
Et après avoir apporté des termes similaires, nous obtenons l'équation quadratique x2 - 3x - 10 \u003d 0. Après l'avoir résolue, nous trouvons les racines x1 \u003d -2; x2 = 5.
Mais nous avons déjà découvert qu'à x = 5, le dénominateur commun x(x - 5) s'annule. Par conséquent, la racine de notre équation
sera x = -2.
§ quatre Bref résumé leçon
Important à retenir :
Lorsque vous résolvez des équations rationnelles fractionnaires, vous devez effectuer les opérations suivantes :
1. Trouvez le dénominateur commun des fractions incluses dans l'équation. De plus, si les dénominateurs des fractions peuvent être décomposés en facteurs, décomposez-les en facteurs, puis trouvez le dénominateur commun.
2. Multipliez les deux côtés de l'équation par un dénominateur commun : trouvez des facteurs supplémentaires, multipliez les numérateurs par des facteurs supplémentaires.
3. Résolvez l'équation entière résultante.
4. Exclure de ses racines celles qui ramènent le dénominateur commun à zéro.
Liste de la littérature utilisée :
- Makarychev Yu.N., N.G. Mindyuk, Neshkov K.I., Suvorova S.B. / Sous la direction de Telyakovsky S.A. Algèbre: manuel. pour 8 cellules. enseignement général établissements. - M. : Éducation, 2013.
- Mordkovitch A.G. Algèbre. 8e année : en deux parties. Partie 1 : Proc. pour l'enseignement général établissements. - M. : Mnémosyne.
- Rurukin A.N. Développements de leçons en algèbre: 8e année. - M.: VAKO, 2010.
- Algèbre 8e année: plans de cours selon le manuel de Yu.N. Makarycheva, N.G. Mindyuk, K.I. Neshkova, S.B. Suvorova / Auth.-comp. TL Afanasiev, L.A. Tapilina. - Volgograd : Enseignant, 2005.
Nous avons introduit l'équation ci-dessus au § 7. Tout d'abord, nous rappelons ce qu'est une expression rationnelle. Il s'agit d'une expression algébrique composée de nombres et de la variable x utilisant les opérations d'addition, de soustraction, de multiplication, de division et d'exponentiation avec un exposant naturel.
Si r(x) est une expression rationnelle, alors l'équation r(x) = 0 est appelée une équation rationnelle.
Cependant, en pratique, il est plus pratique d'utiliser une interprétation un peu plus large du terme "équation rationnelle": il s'agit d'une équation de la forme h(x) = q(x), où h(x) et q(x) sont expressions rationnelles.
Jusqu'à présent, nous ne pouvions résoudre aucune équation rationnelle, mais une seule qui, à la suite de diverses transformations et raisonnements, se réduisait à équation linéaire. Maintenant nos possibilités sont bien plus grandes : nous serons capables de résoudre une équation rationnelle, qui se réduit non seulement à des
mu, mais aussi à l'équation quadratique.
Rappelez-vous comment nous avons résolu les équations rationnelles plus tôt et essayez de formuler un algorithme de solution.
Exemple 1 résous l'équation
Décision. On réécrit l'équation sous la forme
Dans ce cas, comme d'habitude, nous utilisons le fait que les égalités A \u003d B et A - B \u003d 0 expriment la même relation entre A et B. Cela nous a permis de transférer le terme vers le côté gauche de l'équation avec le signe opposé.
Effectuons des transformations du côté gauche de l'équation. Nous avons

Rappel des conditions d'égalité fractions zéro : si, et seulement si, deux relations sont satisfaites simultanément :
1) le numérateur de la fraction est zéro (a = 0) ; 2) le dénominateur de la fraction est différent de zéro).
En égalant à zéro le numérateur de la fraction du côté gauche de l'équation (1), nous obtenons

Il reste à vérifier la réalisation de la deuxième condition mentionnée ci-dessus. Le rapport signifie pour l'équation (1) que . Les valeurs x 1 = 2 et x 2 = 0,6 satisfont les relations indiquées et servent donc de racines à l'équation (1), et en même temps de racines à l'équation donnée.
1) Transformons l'équation sous la forme
![]()
2) Effectuons les transformations du membre gauche de cette équation :

(modifié simultanément les signes du numérateur et
fractions).
De cette façon, équation donnée prend la forme
![]()
3) Résolvez l'équation x 2 - 6x + 8 = 0. Trouvez

4) Pour les valeurs trouvées, vérifier la condition ![]() . Le chiffre 4 satisfait à cette condition, mais pas le chiffre 2. Donc 4 est la racine de l'équation donnée, et 2 est une racine étrangère.
. Le chiffre 4 satisfait à cette condition, mais pas le chiffre 2. Donc 4 est la racine de l'équation donnée, et 2 est une racine étrangère.
Réponse : 4.
2. Solution d'équations rationnelles en introduisant une nouvelle variable
La méthode d'introduction d'une nouvelle variable vous est familière, nous l'avons utilisée plus d'une fois. Montrons par des exemples comment il est utilisé dans la résolution d'équations rationnelles.
Exemple 3 Résolvez l'équation x 4 + x 2 - 20 = 0.
Décision. Nous introduisons une nouvelle variable y \u003d x 2. Puisque x 4 \u003d (x 2) 2 \u003d y 2, alors l'équation donnée peut être réécrite sous la forme
y 2 + y - 20 = 0.
Il s'agit d'une équation quadratique dont nous trouverons les racines à l'aide de l'équation connue formules; on obtient y 1 = 4, y 2 = - 5.
Mais y \u003d x 2, ce qui signifie que le problème a été réduit à résoudre deux équations :
x2=4 ; x 2 \u003d -5.
À partir de la première équation, nous trouvons que la deuxième équation n'a pas de racines.
Réponse: .
Une équation de la forme ax 4 + bx 2 + c \u003d 0 est appelée une équation biquadratique ("bi" - deux, c'est-à-dire, pour ainsi dire, une équation "deux fois carré"). L'équation qui vient d'être résolue était exactement biquadratique. Toute équation biquadratique est résolue de la même manière que l'équation de l'exemple 3 : une nouvelle variable y \u003d x 2 est introduite, l'équation quadratique résultante est résolue par rapport à la variable y, puis renvoyée à la variable x.
Exemple 4 résous l'équation
![]()
Décision. Notez que la même expression x 2 + 3x apparaît deux fois ici. Par conséquent, il est logique d'introduire une nouvelle variable y = x 2 + Zx. Cela nous permettra de réécrire l'équation d'une manière plus simple et beau(ce qui, en fait, est le but d'introduire une nouvelle variable- et l'enregistrement est plus facile
, et la structure de l'équation devient plus claire) :
![]()
Et maintenant, nous allons utiliser l'algorithme pour résoudre une équation rationnelle.
1) Déplaçons tous les termes de l'équation en une seule partie :
![]() = 0
= 0
2) Transformons le côté gauche de l'équation

Nous avons donc transformé l'équation donnée sous la forme

3) À partir de l'équation - 7y 2 + 29y -4 = 0, nous trouvons (nous avons déjà résolu pas mal d'équations quadratiques, donc cela ne vaut probablement pas la peine de toujours donner des calculs détaillés dans le manuel).
4) Vérifions les racines trouvées en utilisant la condition 5 (y - 3) (y + 1). Les deux racines satisfont à cette condition.
Ainsi, l'équation quadratique pour la nouvelle variable y est résolue : ![]()
Puisque y \u003d x 2 + Zx, et y, comme nous l'avons établi, prend deux valeurs : 4 et, - nous devons encore résoudre deux équations : x 2 + Zx \u003d 4 ; x 2 + Zx \u003d. Les racines de la première équation sont les nombres 1 et - 4, les racines de la seconde équation sont les nombres

Dans les exemples considérés, la méthode d'introduction d'une nouvelle variable était, comme aiment à le dire les mathématiciens, adéquate à la situation, c'est-à-dire qu'elle lui correspondait bien. Pourquoi? Oui, car la même expression a été clairement rencontrée plusieurs fois dans l'équation et il était raisonnable de désigner cette expression nouvelle lettre. Mais ce n'est pas toujours le cas, parfois une nouvelle variable "n'apparaît" que dans le processus de transformations. C'est exactement ce qui se passera dans l'exemple suivant.
Exemple 5 résous l'équation
x(x-1)(x-2)(x-3) = 24.
Décision. Nous avons
x (x - 3) \u003d x 2 - 3x;
(x - 1) (x - 2) \u003d x 2 -3x + 2.
Ainsi, l'équation donnée peut être réécrite comme
(x 2 - 3x)(x 2 + 3x + 2) = 24
Maintenant une nouvelle variable est "apparue": y = x 2 - Zx.
Avec son aide, l'équation peut être réécrite sous la forme y (y + 2) \u003d 24 puis y 2 + 2y - 24 \u003d 0. Les racines de cette équation sont les nombres 4 et -6.
En revenant à la variable d'origine x, nous obtenons deux équations x 2 - Zx \u003d 4 et x 2 - Zx \u003d - 6. De la première équation, nous trouvons x 1 \u003d 4, x 2 \u003d - 1; la deuxième équation n'a pas de racines.
Réponse : 4, - 1.
Dans cet article je vais vous montrer algorithmes pour résoudre sept types d'équations rationnelles, qui sont réduits au carré au moyen d'un changement de variables. Dans la plupart des cas, les transformations qui conduisent au remplacement ne sont pas triviales et il est assez difficile de les deviner par vous-même.
Pour chaque type d'équation, j'expliquerai comment y apporter un changement de variable, puis je montrerai une solution détaillée dans le didacticiel vidéo correspondant.
Vous avez la possibilité de continuer à résoudre les équations vous-même, puis de vérifier votre solution avec le didacticiel vidéo.
Alors, commençons.
1 . (x-1)(x-7)(x-4)(x+2)=40
Notez que le produit de quatre parenthèses est sur le côté gauche de l'équation, et le nombre est sur le côté droit.
1. Regroupons les parenthèses par deux pour que la somme des termes libres soit la même.
2. Multipliez-les.
3. Introduisons un changement de variable.
Dans notre équation, nous regroupons la première tranche avec la troisième, et la seconde avec la quatrième, puisque (-1) + (-4) \u003d (-7) + 2 :
![]()
À ce stade, le changement de variable devient évident :
On obtient l'équation ![]()
Réponse: ![]()
2 .
Une équation de ce type est similaire à la précédente avec une différence : à droite de l'équation se trouve le produit d'un nombre par. Et il est résolu d'une manière complètement différente:
1. Nous regroupons les parenthèses par deux pour que le produit des termes libres soit le même.
2. Nous multiplions chaque paire de parenthèses.
3. De chaque facteur, nous retirons x de la parenthèse.
4. Divisez les deux membres de l'équation par .
5. On introduit un changement de variable.
Dans cette équation, on regroupe la première tranche avec la quatrième, et la seconde avec la troisième, puisque :
Notez que dans chaque tranche le coefficient at et le terme libre sont les mêmes. Retirons le multiplicateur de chaque parenthèse :
Puisque x=0 n'est pas la racine de l'équation d'origine, nous divisons les deux côtés de l'équation par . On a:
![]()
![]()
On obtient l'équation : ![]()
Réponse: ![]()
3
. ![]()
Notez que les dénominateurs des deux fractions contiennent trinômes carrés, dont le coefficient directeur et le terme libre sont identiques. Nous retirons, comme dans l'équation du deuxième type, x de la parenthèse. On a:

Divisez le numérateur et le dénominateur de chaque fraction par x :

On peut maintenant introduire un changement de variable :
On obtient l'équation pour la variable t :
4 .
Notez que les coefficients de l'équation sont symétriques par rapport au central. Une telle équation est appelée consigné .
Pour le résoudre
1. Divisez les deux membres de l'équation par (Nous pouvons le faire puisque x=0 n'est pas la racine de l'équation.) Nous obtenons :
![]()
2. Regroupez les termes de cette manière :

3. Dans chaque groupe, on sort le facteur commun :

4. Introduisons un remplacement :
5. Exprimons l'expression en fonction de t :
D'ici ![]()
On obtient l'équation pour t :
![]()
Réponse:
5. Équations homogènes.
Des équations ayant la structure d'une équation homogène peuvent être rencontrées lors de la résolution d'équations exponentielles, logarithmiques et équations trigonométriques, il faut donc le reconnaître.
Les équations homogènes ont la structure suivante :
Dans cette égalité, A, B et C sont des nombres, et les mêmes expressions sont indiquées par un carré et un cercle. Autrement dit, sur le côté gauche de l'équation homogène se trouve la somme des monômes qui ont le même degré (en ce cas le degré des monômes est 2), et il n'y a pas de terme libre.
Pour résoudre l'équation homogène, on divise les deux côtés par
Attention! Lorsque vous divisez les côtés droit et gauche de l'équation par une expression contenant une inconnue, vous pouvez perdre les racines. Par conséquent, il est nécessaire de vérifier si les racines de l'expression par laquelle nous divisons les deux parties de l'équation sont les racines de l'équation d'origine.
Allons-y par le premier chemin. On obtient l'équation :
Maintenant, nous introduisons une substitution de variable :
Simplifiez l'expression et obtenez une équation biquadratique pour t :
![]()
Réponse: ou alors
7
. 
Cette équation a la structure suivante :
Pour le résoudre, vous devez sélectionner le carré complet sur le côté gauche de l'équation.
Pour sélectionner un carré complet, vous devez ajouter ou soustraire le produit double. Ensuite, nous obtenons le carré de la somme ou de la différence. Ceci est essentiel pour une substitution de variable réussie.
Commençons par trouver le produit double. Ce sera la clé pour remplacer la variable. Dans notre équation, le produit double est
![]()
Voyons maintenant ce qui nous convient le mieux - le carré de la somme ou de la différence. Considérons, pour commencer, la somme des expressions :
Excellent! cette expression est exactement égale à deux fois le produit. Ensuite, pour obtenir le carré de la somme entre parenthèses, il faut additionner et soustraire le produit double :
