Que signifie prouver un exemple d'identité. Équations
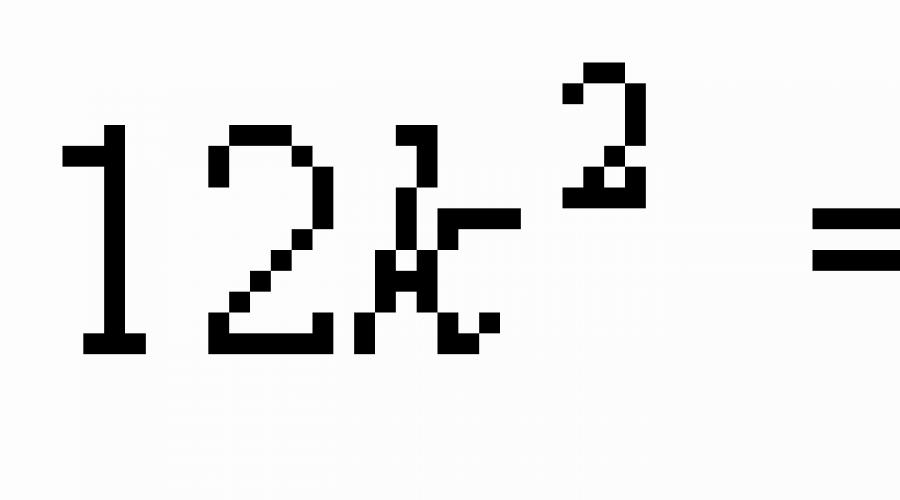
Lire aussi
CONFÉRENCE N°3 Preuve d'identité
Objectif : 1. Répéter les définitions de l'identité et à l'identique expressions égales.
2.Introduire le concept de transformation identique des expressions.
3. Multiplier un polynôme par un polynôme.
4. Factoriser un polynôme à l'aide de la méthode de regroupement.
Que chaque jour et chaque heure
Il nous apportera quelque chose de nouveau,
Que notre esprit soit bon,
Et le cœur sera intelligent !
Il existe de nombreux concepts en mathématiques. L’un d’eux est l’identité.
Une identité est une égalité qui vaut pour toutes les valeurs des variables qui y sont incluses. Nous connaissons déjà certaines identités.
Par exemple, tout le monde formules de multiplication abrégées sont des identités.
Formules de multiplication abrégées
1. (un ± b)2 = un 2 ± 2 un B + b 2,
2. (un ± b)3 = un 3 ± 3 un 2b + 3un B 2 ± b 3,
3. un 2 - b 2 = (un - b)(un + b),
4. un 3 ± b 3 = (un ± b)(un 2 un B + b 2).
Prouver son identité- cela revient à établir que pour toute valeur de variable valide, son côté gauche est égal au côté droit.
Il y en a plusieurs en algèbre de diverses façons preuves d'identité.
Méthodes de preuve d'identité
- Effectuer des conversions équivalentes côté gauche de l’identité. Si l’on se retrouve avec le côté droit, alors l’identité est considérée comme prouvée. Effectuer des conversions équivalentes le côté droit de l’identité. Si nous finissons par obtenir côté gauche, alors l'identité est considérée comme prouvée. Effectuer des conversions équivalentes côtés gauche et droit de l’identité. Si nous obtenons le même résultat, alors l’identité est considérée comme prouvée. Du côté droit de l’identité, nous soustrayons le côté gauche. Nous effectuons des transformations équivalentes sur la différence. Et si au final nous obtenons zéro, alors l’identité est considérée comme prouvée. Le côté droit est soustrait du côté gauche de l’identité. Nous effectuons des transformations équivalentes sur la différence. Et si au final nous obtenons zéro, alors l’identité est considérée comme prouvée.
Il convient également de rappeler que l'identité n'est valable que pour les valeurs admissibles des variables.
Comme vous pouvez le constater, il existe de nombreuses façons. Quelle méthode choisir dans ce domaine cas spécifique, dépend de l’identité que vous devez prouver. Au fur et à mesure que vous prouverez diverses identités, vous acquerrez de l’expérience dans le choix d’une méthode de preuve.
Une identité est une équation satisfaite de manière identique, c'est-à-dire valable pour toutes les valeurs admissibles des variables qui y sont incluses. Prouver une identité signifie établir que pour tous valeurs acceptables variables, ses côtés gauche et droit sont égaux.
Moyens de prouver votre identité :
1. Effectuez des transformations sur le côté gauche et obtenez finalement le côté droit.
2. Effectuez des transformations sur le côté droit et obtenez finalement le côté gauche.
3. Transformez séparément les côtés droit et gauche et obtenez la même expression dans le premier et le deuxième cas.
4. Composez la différence entre les côtés gauche et droit et, grâce à ses transformations, obtenez zéro.
Regardons quelques exemples simples
Exemple 1. Prouver l'identité x·(a+b) + a·(b-x) = b·(a+x).
Solution.
Puisque le côté droit a une petite expression, essayons de transformer le côté gauche en égalité.
x·(a+b) + a·(b-x) = x·a +x·b + a·b – a·x.
Présentons des termes similaires et retirons le facteur commun de la parenthèse.
x a + x b + a b – a x = x b + a b = b (a + x).
Nous avons constaté que le côté gauche après les transformations est devenu le même que le côté droit. Cette égalité est donc une identité.
Exemple 2. Prouvez l’identité : un² + 7·un + 10 = (un+5)·(un+2).
Solution:
Dans cet exemple, vous pouvez procéder de la manière suivante. Ouvrons les parenthèses du côté droit de l'égalité.
(a+5)·(a+2) = (a²) + 5·a +2·a +10 = a²+7·a + 10.
Nous voyons qu'après les transformations, le côté droit de l'égalité est devenu le même que le côté gauche de l'égalité. Cette égalité est donc une identité.
« Le remplacement d’une expression par une autre identiquement égale à elle s’appelle une transformation identique de l’expression »
Découvrez quelle égalité est une identité :
1. - (une – c) = - une – c ;
2. 2 · (x + 4) = 2x – 4;
3. (x – 5) · (-3) = - 3x + 15.
4. рху (- р2 x2 y) = - р3 x3 y3.
"Pour prouver qu'une certaine égalité est une identité, ou, comme on dit autrement, pour prouver une identité, on utilise des transformations identiques d'expressions"
Une égalité vraie pour toutes les valeurs des variables est appelée identité. Prouver qu'une certaine égalité est une identité, ou, comme on dit autrement, pour que prouver son identité, utilisez des transformations identiques d'expressions.
Prouvons l'identité :
xy - 3y - 5x + 16 = (x - 3)(y - 5) + 1 Transformez le côté gauche de cette égalité :
xy - 3y - 5x + 16 = (xy - 3y) + (- 5x + 15) +1 = y(x - 3) - 5(x -3) +1 = (y - 5)(x - 3) + 1 En conséquence transformation de l'identité du côté gauche du polynôme nous avons obtenu son côté droit et avons ainsi prouvé que cette égalité est identité.
Pour des preuves d'identité transformer son côté gauche en droit ou son côté droit en gauche, ou montrer que les côtés gauche et droit de l'égalité originale sont identiquement égaux à la même expression.
Multiplier un polynôme par un polynôme
Multiplions le polynôme a+bà un polynôme c + d. Composons le produit de ces polynômes :
(a+b)(c+d).
Notons le binôme a+b lettre X et transformer le produit obtenu selon la règle de multiplication d'un monôme par un polynôme :
(a+b)(c+d) = x(c+d) = xc + xd.
En expression xc + xd. substituons X polynôme a+b et utilisez à nouveau la règle pour multiplier un monôme par un polynôme :
xc + xd = (a+b)c + (a+b)d = ac + bc + ad + bd.
Donc: (a+b)(c+d) = ac + bc + ad + bd.
Produit de polynômes a+b Et c + d nous l'avons représenté comme un polynôme ac + bc + annonce + bd. Ce polynôme est la somme de tous les monômes résultant de la multiplication de chaque terme du polynôme a+b pour chaque terme du polynôme c + d.
Conclusion:
le produit de deux polynômes quelconques peut être représenté comme un polynôme.
Règle:
Pour multiplier un polynôme par un polynôme, vous devez multiplier chaque terme d'un polynôme par chaque terme d'un autre polynôme et additionner les produits résultants.
Notez que lors de la multiplication d'un polynôme contenant m termes d'un polynôme contenant n termes dans le produit, avant d'apporter des termes similaires, le résultat doit être minute membres. Cela peut être utilisé pour le contrôle.
Factoriser un polynôme à l'aide de la méthode de regroupement :
Auparavant, nous avons appris à factoriser un polynôme en retirant le facteur commun des parenthèses. Parfois, il est possible de factoriser un polynôme en utilisant une autre méthode - regroupement de ses membres.
Factorisons le polynôme
ab - 2b + 3a - 6 Regroupons-le pour que les termes de chaque groupe aient un facteur commun et retirons ce facteur entre parenthèses :
ab - 2b + 3a - 6 = (ab - 2b) + (3a - 6) = b(a - 2) + 3(a - 2) Chaque terme de l'expression résultante a un facteur commun (a - 2). Sortons ce facteur commun des parenthèses :
b(a - 2) + 3(a - 2) = (b +3)(a - 2) En conséquence, nous avons factorisé le polynôme d'origine :
ab - 2b + 3a - 6 = (b +3)(a - 2) La méthode que nous avons utilisée pour factoriser le polynôme s'appelle méthode de regroupement.
Expansion polynomiale ab-2b + 3a-6 la factorisation peut être effectuée en regroupant ses termes différemment :
ab - 2b + 3a - 6 = (ab + 3a) + (- 2b - 6) = a(b + 3) -2(b + 3) = (a - 2)(b + 3)
Répéter:
1. Méthodes de preuve d'identité.
2. Ce qu'on appelle la transformation identitaire d'une expression.
3. Multiplier un polynôme par un polynôme.
4. Factorisation d'un polynôme à l'aide de la méthode de regroupement
Objectif d'apprentissage:
répéter les définitions des équations, des identités ;
apprendre à distinguer les concepts d'équation et d'identité ;
identifier les moyens de prouver les identités ;
répéter les méthodes de réduction d'un monôme en vue générale, ajout de polynômes, multiplication d'un monôme par un polynôme lors de la preuve d'identités.
Objectif de développement :
développer le discours mathématique compétent des élèves (enrichir et compliquer lexique lors de l'utilisation de termes mathématiques spéciaux),
développer la réflexion : la capacité de comparer, d'analyser, de faire des analogies, de prédire, de tirer des conclusions (lors du choix des méthodes de preuve d'identité) ;
développer les compétences pédagogiques et cognitives des élèves.
Objectif pédagogique :
développer la capacité de travailler en groupe, de coordonner vos activités avec les autres participants au processus éducatif ;
cultiver la tolérance.
Type de cours : application globale des connaissances.
Étapes du cours : préparatoire, application des connaissances, résultat.
La frontière entre connaissance et ignorance :
peut appliquer des opérations de réduction d'un monôme à une forme standard ;
addition de polynômes, multiplication d'un polynôme par un polynôme.
Distinguer les notions d'équation et d'identité ;
effectuer des justificatifs d'identité ;
choisir et appliquer rationnellement des méthodes pour prouver son identité.
Travail de façade
Verbal
Visuel
Application des connaissances (assurer l'assimilation de nouvelles connaissances et méthodes d'action au niveau de l'application en situation d'apprentissage modifiée)
Basé sur les transformations des côtés gauche et droit du donné
égalité mathématique, identifier les moyens de prouver les identités ;
Révéler manière rationnelle parmi ceux proposés et élaborer la sélection décision rationnelle selon une condition d'identité donnée
Travail de groupe
Recherche
Pratique
Résultat (analyse et évaluation du succès dans la réalisation de l'objectif)
Résumer le travail de la leçon en faisant travail individuel, où il est proposé de sélectionner une identité parmi les égalités présentées et de la prouver par l'une des méthodes proposées (de préférence rationnelle) ;
Ensuite, les élèves auto-évaluent leur travail pendant la leçon selon les critères donnés (dès le début de la leçon).
Frontale
Verbal
Résumé de la leçon (brièvement) :
1. Étape (préparatoire)
Considérons la notation mathématique : (travail de façade)
En règle générale, les élèves de 7e croient qu'il s'agit d'une équation et, en la résolvant, ils obtiennent une équation linéaire de la forme : 0 x = 0, vraie pour tout x.
Ensuite, l'enseignant montre le travail d'une autre classe, et les enfants sont confrontés à une contradiction : dans le travail d'une autre classe, les élèves prouvent qu'il s'agit d'une identité.
Conclusion: il faut prêter attention au fait que la même égalité peut être considérée comme une identité et comme une équation. Cela dépend de la condition d'un travail donné : si vous devez établir à quelle valeur d'une variable se produit l'égalité, alors ceci- l'équation. Et si vous devez prouver que l'égalité est valable pour toutes les valeurs des variables -identité.
2. Étape (candidature)
Identifier les moyens de prouver les identités : (travail de groupe)
L'expression s'écrit :
Tâche pratique en groupe pour identifier les moyens de prouver les identités :
Suivre les règles de travail en groupe (elles sont imprimées sur des panneaux placés par l'enseignant aux postes de travail des élèves)
Sur papier Whatman, dans le cadre d'un travail commun, effectuez quelques transformations en utilisant une certaine technologie spécifiée dans le devoir de groupe et prouvez que l'expression donnée ne dépend pas des valeurs des variables, et est donc une identité ;
Donner une explication du travail effectué et tirer une conclusion : quel est le cette méthode des preuves d'identité;
Groupe Tâche 1 :
Déplacez le côté droit de l’équation vers la gauche. Montrer que cette expression ne dépend pas des valeurs des variables.
Groupe Tâche 2 :
Transformez le côté gauche de l’égalité. Montrer qu'elle est égale à la bonne, ce qui signifie que cette expression ne dépend pas des valeurs des variables.
Tâche pour le groupe 3 :
Transformez simultanément les côtés gauche et droit de l’équation. Montrer que cette égalité ne dépend pas des valeurs des variables.
Lorsque l'on considère le travail effectué par les enfants pour prouver leur identité, il convient de représenter les résultats des méthodes utilisées sous forme de diagrammes sur des feuilles de papier séparées, avec un indicateur numérique, afin que plus tard, ces diagrammes puissent être utilisés non seulement dans cela, mais aussi dans d'autres cours d'algèbre.
3. Étape (résultat)
a) Identités pour choisir une solution rationnelle : (travail de façade)
5)
![]()
Professeur: Afonasova Irina Olegovna
Sujet : algèbre
Niveau : 7e année
Type de cours : apprendre du nouveau matériel
Sujet: Preuve d'identité
Objectifs de la leçon:
- Répétez les définitions de l'identité et des expressions identiquement égales, transformation identique des expressions.
- Formation de l'habileté à choisir une méthode de preuve d'identité en utilisant la méthode de transformation à l'identique des expressions.
- Favoriser une culture de communication parmi les étudiants.
Pendant les cours
1 . Étape organisationnelle de la leçon
Avant le début du cours, les élèves de la classe sont répartis en six groupes d'étude composition mixte.
Professeur : Bonjour les gars, je propose de transformer la salle d'étude enlaboratoire de recherche, et toi et moi dans Master ès sciences en sciences mathématiques.
Mais tout scientifique qui se respecte décide constamment de problème important, il faut donc avant tout découvrir : sur quel problème allons-nous travailler aujourd'hui ?
2. Déterminer le sujet de la leçon
Pour ce faire, considérons les expressions 2x+y et 2xy. Trouvons les valeurs des expressions pour x=1 et y=2.
professeur b suggère d'aller au tableauà l'étudiant et décider cette tâche, etformuler une conclusion: lorsque x=1 et y=2, les expressions prennent des valeurs égales (4).
Professeur: Cependant, vous pouvez spécifier des valeurs des variables x et y telles que les valeurs de ces expressions ne soient pas égales. Par exemple, x=3, y=4.
Étudiant , debout au tableau, le vérifie.
Professeur: Considérons maintenant les expressions 3(x+y) et 3x+3y. Trouvons les valeurs des expressions pour x=5 et y=4.
Étudiant, debout au tableau : résoudre un problème, formuler une conclusion.
Professeur: Pour toutes les valeurs des variables, les valeurs de ces expressions sont-elles égales ? Si oui, pourquoi?
Étudiant réponses. (Réponse : Oui, selon la propriété distributive de la multiplication).
L'enseignant invite la classe à retenir le nom de telles expressions, le nom de leur égalité.
Après cela, diapositive 1.
Puis le professeur demande : « Quel est le sujet de la leçon d’aujourd’hui. »
Professeur : Aujourd'hui, nous allons travailler sur la « Preuve d'Identité ».
Le sujet de la leçon s'écrit : « Preuve d'identités » ( Diapositive2)
Professeur : D'accord, maintenant testons-nous. Des égalités apparaîtront à l'écran, si cette égalité est une identité, alors je vous invite à lever la main. ( Diapositive 3)
- - (a – c) = - a + c (oui)
- a (b + c) = ab – ac (non)
- une – (b + c) = une – b + c(Non)
- (une + b) – c = une – c + c(Oui)
- - (a + b) = - a – b (oui)
3. Déterminer le but de la leçon
Professeur : D'accord, il est maintenant temps pour nous de passer du statut de théoriciens à celui de scientifiques pratiques, mais pour cela, nous devons découvrir ce que nous devons utiliser pourprouver son identité, et ici nous ne pouvons pas nous passer de la littérature scientifique ; nous trouverons la réponse à cette question à la page 18 de votre manuel. Les élèves trouvent la réponse dans le manuel :"Pour prouver qu'une certaine égalité est une identité, utilisez des transformations identiques d'expressions". Les participants des autres groupes indiquent leur accord ou leur désaccord avec les signaux spéciaux évoqués ci-dessus. ( Diapositive 4)
Professeur : Bravo, mais maintenant la question suivante se pose, qu'est-ce quetransformation identitaire des expressions?
« Le remplacement d’une expression par une autre identiquement égale à elle s’appelle une transformation identique de l’expression »(l'enseignant invite l'un des participants de n'importe quel groupe à répondre à cette question) ( Diapositive 5)
Professeur : Alors, quel est le but de la leçon ? Les élèves citent l'un de leurs objectifs : apprendre à prouver des identités à l'aide de transformations identiques d'expressions.
4. Identifier un moyen de prouver les identités en utilisant la méthode de transformation à l'identique des expressions
Enseignant : Maintenant, nous sommes déjà « mûrs » pour Travaux pratiques, et je vous demanderais de porter votre attention sur carte . Mission : « Prouver l'identité », chaque groupe de scientifiques a reçu un exemple qu'il doit résoudre de manière indépendante si des difficultés surviennent, des cartes de consultant viendront à la rescousse ;
Cartes de tâches
Carte 1
Carte 2
Carte 3
Carte 4
Carte 5
Carte 6
Nous devons maintenant protéger notre travail. (Présentation des travaux réalisés au tableau, les membres volontaires du groupe prennent la parole)
Professeur : Super, et maintenant, chers collègues, il est temps de résumer, que devons-nous faire pour prouver que l’égalité est identité ? Réponses suggérées aux élèves : ( Diapositive 6)
- Écrivez le côté gauche de l'égalité, transformez-le et assurez-vous qu'il est égal au côté droit.
ou - Notez le côté droit de l'égalité, transformez-le et assurez-vous qu'il est égal au côté gauche.
ou - Transformez les côtés gauche et droit de l’égalité et assurez-vous qu’ils sont égaux à la même expression.
Professeur : Quelle conclusion peut-on tirer dans le cas où tout ce que nous venons de dire ne se réalisera pas ? Réponse suggérée aux élèves :L'égalité ne sera pas l'identité.
5. Résumer la leçon.
Avons-nous réussi à atteindre notre objectif ? ….
Professeur : Pour pérenniser les connaissances acquises, nous poursuivrons ce travail chez nous :Devoirs(Diapositive 7) :
N° 691(a), 692(a), 715(a), tâche créative(facultatif) : * Faire 3 égalités qui seront une identité (illustrer chaque méthode de preuve).
Professeur : Et maintenant place à la créativité : Dans le poème que vous voyez, insérez les mots manquants ( Diapositive 8) :
Il y a toutes sortes d'égalités, frères,
Et bien sûr, tout le monde le sait.
Il y a – avec des variables, il y a – (numérique),
Très, très complexe (simple)
Mais parmi les égalités, il existe une classe spéciale,
Nous allons maintenant raconter notre histoire à son sujet.
C’est ce qu’on appelle l’égalité (identitaire).
Mais il nous reste encore à le prouver.
Pour ce faire, il suffit de prendre
Et l'égalité est (convertir)
Bien sûr, il ne nous sera pas difficile de le savoir
Quelle partie devrons-nous changer ?
Ou peut-être que nous devrons changer les deux,
Par égalité d'esprit, ce n'est pas difficile (à comprendre)
Hourra! Nous avons pu appliquer nos connaissances
Conversion d'égalité terminée.
Et nous disons hardiment la réponse :
Alors, est-ce une identité, ou pas !
Professeur : Merci pour la leçon !
Aperçu:
Cartes de tâches
Légendes des diapositives :
Définition de l'identité : Une identité est une égalité qui est vraie pour toutes les valeurs admissibles des variables qui y sont incluses. Définition d'expressions identiquement égales : Deux expressions dont les valeurs correspondantes sont égales pour toutes les valeurs des variables sont dites identiquement égales.
Preuve d'identité
Exemples d'identités : - (a – b) = - a + b a (b + c) = ab - ac a – (b + c) = a – b + c (a + b) – c = a – c + b - (une + b) = - une - b
Que devez-vous utiliser pour prouver l’identité ? Pour prouver qu'une certaine égalité est une identité, ou, comme on dit autrement, pour prouver une identité, on utilise des transformations identiques d'expressions.
Transformation à l'identique d'une expression Le remplacement d'une expression par une autre qui lui est identiquement égale est appelé transformation à l'identique d'une expression.
Pour prouver qu'une égalité est une identité, il faut : Écrire le côté gauche de l'égalité, le transformer et s'assurer qu'il est égal au côté droit. ou Notez le côté droit de l'égalité, transformez-le et assurez-vous qu'il est égal au côté gauche. ou Transformez à tour de rôle les deux côtés de l'égalité et assurez-vous qu'ils sont égaux à la même expression.
Devoir : N° 691(a), N° 692(a), N° 694, Composez 3 égalités qui seront une identité. *
Il y a toutes sortes d’égalités, mes frères, et bien sûr tout le monde le sait. Il y a - avec des variables, il y a -... Très, très complexe... . Mais parmi les égalités, il existe une classe spéciale dont nous allons maintenant raconter notre histoire. ... c'est ce qu'on appelle l'égalité, mais encore faut-il le prouver. Pour ce faire, il suffit de prendre Et l’égalité est…. Il ne nous sera bien sûr pas difficile de savoir quelle partie nous devrons changer, Ou peut-être devrons-nous changer les deux, Selon l'égalité des espèces, ce ne sera pas difficile... Hourra ! Nous avons réussi à appliquer nos connaissances. La transformation de l’égalité est terminée. Et nous répondons avec audace : cette identité est-elle ainsi, ou n'est-elle toujours pas ?
Équations
Comment résoudre des équations ?
Dans cette section nous rappellerons (ou étudierons, selon qui vous choisirez) les équations les plus élémentaires. Alors quelle est l’équation ? Dans le langage humain, il s'agit d'une sorte d'expression mathématique où il y a un signe égal et une inconnue. Ce qui est généralement désigné par la lettre "X". Résous l'équation- il s'agit de trouver de telles valeurs de x qui, une fois substituées dans original l’expression nous donnera l’identité correcte. Permettez-moi de vous rappeler que l'identité est une expression qui ne fait aucun doute même pour une personne qui n'est absolument pas chargée de connaissances mathématiques. Comme 2=2, 0=0, ab=ab, etc. Alors comment résoudre des équations ? Voyons cela.
Il existe toutes sortes d’équations (je suis surpris, non ?). Mais toute leur infinie variété peut être divisée en quatre types seulement.
4. Autre.)
Tous les autres, bien sûr, et surtout, oui...) Cela inclut à la fois les cubes et les démonstratif, Et logarithmique, Et trigonométrique et toutes sortes d'autres. Nous travaillerons en étroite collaboration avec eux dans les sections appropriées.
Je dirai tout de suite que parfois les équations du premier trois types ils vous tromperont tellement que vous ne les reconnaîtrez même pas... Rien. Nous apprendrons comment les dérouler.
Et pourquoi avons-nous besoin de ces quatre types ? Et maintenant quoi équations linéaires résolu d'une manière carré autres, rationnels fractionnaires - troisième, UN repos Ils n’osent pas du tout ! Eh bien, ce n’est pas qu’ils ne peuvent pas du tout décider, c’est que je me suis trompé en mathématiques.) C’est juste qu’ils ont leurs propres techniques et méthodes spéciales.
Mais pour tout (je le répète - pour n'importe lequel!) les équations fournissent une base de résolution fiable et sûre. Fonctionne partout et toujours. Cette fondation... Cela semble effrayant, mais c'est très simple. Et très (Très!) important.
En fait, la solution de l’équation consiste précisément en ces transformations. 99% Réponse à la question : " Comment résoudre des équations ?" réside précisément dans ces transformations. L'indice est-il clair ?)
Transformations identiques d'équations.
DANS toutes les équations Pour trouver l’inconnu, vous devez transformer et simplifier l’exemple original. Et pour qu'au changement apparence l’essence de l’équation n’a pas changé. De telles transformations sont appelées identique ou équivalent.
Notez que ces transformations s'appliquent spécifiquement aux équations. En mathématiques, il y a aussi transformations identitaires expressions. C'est un autre sujet.
Maintenant, nous allons répéter tout, tout, tout de base transformations identiques d'équations.
Basiques car ils peuvent être appliqués à n'importe lequeléquations - linéaire, carré, fractionnaire trigonométrique, indicatif, logarithmique etc. et ainsi de suite.
Première transformation identitaire : vous pouvez ajouter (soustraire) les deux côtés de n'importe quelle équation n'importe lequel(mais un seul et même !) nombre ou expression (y compris une expression avec une inconnue !). Cela ne change pas l’essence de l’équation.
D'ailleurs, vous avez constamment utilisé cette transformation, vous pensiez juste que vous transfériez certains termes d'une partie de l'équation à une autre avec un changement de signe. Taper:
Le cas est familier, on déplace les deux vers la droite, et on obtient :
![]()
En fait, tu emporté des deux côtés de l’équation est deux. Le résultat est le même:
x+2 - 2 = 3 - 2
Déplacer les termes vers la gauche et la droite avec un changement de signe n’est qu’une version abrégée de la première transformation identitaire. Et pourquoi avons-nous besoin de connaissances aussi approfondies ? - tu demandes. Rien dans les équations. Pour l'amour de Dieu, supportez-le. N'oubliez pas de changer le signe. Mais en inégalités l'habitude du transfert peut conduire à une impasse...
Deuxième transformation identitaire: les deux côtés de l'équation peuvent être multipliés (divisés) par la même chose non nul nombre ou expression. Ici, une limitation compréhensible apparaît déjà : multiplier par zéro est stupide, et diviser est totalement impossible. C'est la transformation que vous utilisez lorsque vous résolvez quelque chose de cool comme
Il est clair X= 2. Comment l'avez-vous trouvé ? Par sélection ? Ou est-ce que cela vous vient tout juste de comprendre ? Afin de ne pas sélectionner et de ne pas attendre un aperçu, vous devez comprendre que vous êtes simplement divisé les deux côtés de l'équation par 5. Lors de la division du côté gauche (5x), le cinq a été réduit, laissant X pur. C'est exactement ce dont nous avions besoin. Et en divisant le côté droit de (10) par cinq, nous obtenons, vous savez, deux.
C'est tout.
C'est drôle, mais ces deux (seulement deux !) transformations identiques sont la base de la solution toutes les équations mathématiques. Ouah! Il est logique de regarder des exemples de quoi et comment, n'est-ce pas ?)
Exemples de transformations identiques d'équations. Problèmes principaux.
Commençons avec d'abord transformation identitaire. Transférer gauche-droite.
Un exemple pour les plus jeunes.)
Disons que nous devons résoudre l'équation suivante :
3-2x=5-3x
Rappelons le sort : "avec X - à gauche, sans X - à droite !" Ce sort est une instruction pour utiliser la première transformation d'identité.) Quelle est l'expression avec un X à droite ? 3x? La réponse est incorrecte ! A notre droite - 3x! Moins trois x ! Par conséquent, en vous déplaçant vers la gauche, le signe deviendra plus. Il s'avérera :
3-2x+3x=5
Ainsi, les X ont été rassemblés en tas. Passons aux chiffres. Il y a un trois à gauche. Avec quel signe ? La réponse « sans aucun » n'est pas acceptée !) Devant les trois, en effet, rien n'est tiré au sort. Et cela veut dire qu'avant les trois il y a plus. Les mathématiciens étaient donc d’accord. Rien n'est écrit, ce qui veut dire plus. Le triple sera donc transféré du côté droit avec un moins. On a:
-2x+3x=5-3
Il ne reste que des bagatelles. A gauche - apportez des similaires, à droite - comptez. La réponse vient tout de suite :
Dans cet exemple, une seule transformation d’identité suffisait. Le deuxième n'était pas nécessaire. Bien, OK.)
Un exemple pour les enfants plus âgés.)
Si vous aimez ce site...
Au fait, j'ai quelques autres sites intéressants pour vous.)
Vous pouvez vous entraîner à résoudre des exemples et découvrir votre niveau. Test avec vérification instantanée. Apprenons - avec intérêt !)
Vous pouvez vous familiariser avec les fonctions et les dérivées.