À quoi est égal le cosinus alpha ? Formules pour angles doubles et ajout d'arguments. Graphique de la fonction cotangente, y = ctg x
Lire aussi
Centré au point A.
α est l'angle exprimé en radians.
Tangente ( bronzage α) est une fonction trigonométrique dépendant de l'angle α entre l'hypoténuse et la jambe triangle rectangle, égal au rapport longueur du côté opposé |BC| à la longueur de la jambe adjacente |AB| .
Cotangente ( ctg α) est une fonction trigonométrique dépendant de l'angle α entre l'hypoténuse et la branche d'un triangle rectangle, égal au rapport de la longueur de la branche adjacente |AB| à la longueur de la jambe opposée |BC| .
Tangente
Où n- entier.
Dans la littérature occidentale, la tangente est notée comme suit :
.
;
;
.
Graphique de la fonction tangente, y = tan x
Cotangente
Où n- entier.
Dans la littérature occidentale, la cotangente est notée comme suit :
.
Les notations suivantes sont également acceptées :
;
;
.
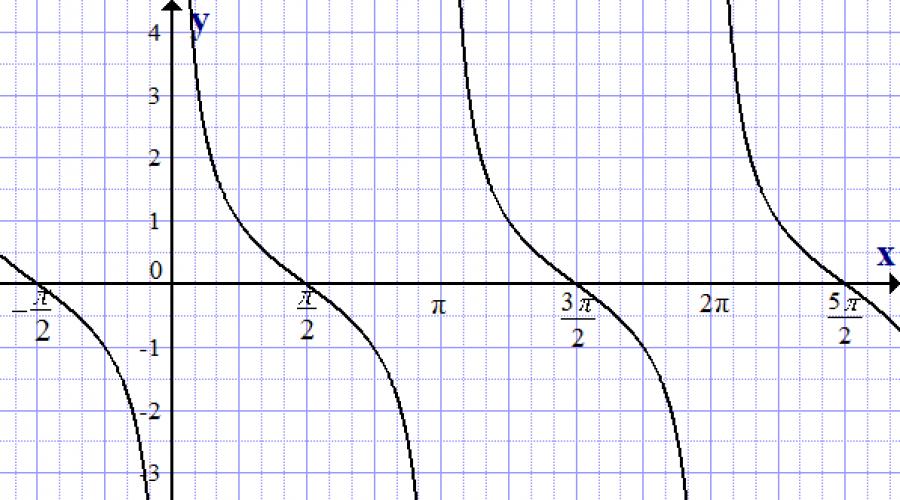
Graphique de la fonction cotangente, y = ctg x

Propriétés de la tangente et de la cotangente
Périodicité
Fonctions y = tgx et y = ctg x sont périodiques de période π.
Parité
Les fonctions tangente et cotangente sont impaires.
Zones de définition et de valeurs, croissantes, décroissantes
Les fonctions tangente et cotangente sont continues dans leur domaine de définition (voir preuve de continuité). Les principales propriétés de la tangente et de la cotangente sont présentées dans le tableau ( n- entier).
| y = tgx | y = ctg x | |
| Portée et continuité | ||
| Plage de valeurs | -∞ < y < +∞ | -∞ < y < +∞ |
| En augmentant | - | |
| Descendant | - | |
| Extrêmes | - | - |
| Des zéros, y = 0 | ||
| Intercepter les points avec l'axe des ordonnées, x = 0 | y = 0 | - |
Formules
Expressions utilisant le sinus et le cosinus
;
;
;
;
;
Formules pour la tangente et la cotangente à partir de la somme et de la différence
Les formules restantes sont faciles à obtenir, par exemple
Produit de tangentes
Formule pour la somme et la différence des tangentes
Ce tableau présente les valeurs des tangentes et des cotangentes pour certaines valeurs de l'argument. 
Expressions utilisant des nombres complexes
Expressions via des fonctions hyperboliques
;
;
Dérivés
; .
.
Dérivée du nième ordre par rapport à la variable x de la fonction :
.
Dériver des formules pour la tangente > > > ; pour cotangente > > >
Intégrales
Extensions de série
Pour obtenir le développement de la tangente en puissances de x, il faut prendre plusieurs termes du développement en série de puissance pour les fonctions péché x Et parce que x et divisez ces polynômes les uns par les autres, . Cela produit les formules suivantes.
À .
à .
Où Bn- Les nombres de Bernoulli. Ils sont déterminés soit à partir de la relation de récurrence :
;
;
Où .
Ou selon la formule de Laplace : 
Fonctions inverses
Les fonctions inverses de tangente et de cotangente sont respectivement arctangente et arccotangente.
Arctangente, arctg
, Où n- entier.
Arccotangente, arcctg
, Où n- entier.
Les références:
DANS. Bronstein, KA (2004). Semendyaev, Manuel de mathématiques pour ingénieurs et étudiants, « Lan », 2009.
G. Korn, Manuel de mathématiques pour travailleurs scientifiques et ingénieurs, 2012.
- 2. Plage de valeurs : [-1;1]
- 3. Fonction étrange.
- 7. Intervalles sur lesquels la fonction est positive : (2*pi*n; pi+2*pi*n)
- 8. Intervalles sur lesquels la fonction est négative : (-pi + 2*pi*n; 2*pi*n)
- 9. Intervalles croissants : [-pi/2 +2*pi*n ; pi/2 +2*pi*n]
- 10. Intervalles décroissants :
- 11. Points minimum : -pi/2 +2*pi*n
- 12. Fonction minimale : -1
- 13. Points maximum : pi/2 +2*pi*n
- 14. Fonction maximale : 1
Propriétés du cosinus
.jpg)
- 1. Zone de définition : axe des nombres entier
- 2. Plage de valeurs : [-1;1]
- 3. Même fonction.
- 4. Plus petite période positive : 2*pi
- 5. Coordonnées des points d'intersection du graphe de fonctions avec l'axe Ox : (pi/2 +pi*n; 0)
- 6. Coordonnées des points d'intersection du graphe de fonctions avec l'axe Oy : (0;1)
- 7. Intervalles auxquels la fonction est positive : (-pi/2 +2*pi*n ; pi/2 +2*pi*n)
- 8. Intervalles auxquels la fonction est négative : (pi/2 +2*pi*n ; 3*pi/2 +2*pi*n)
- 9. Intervalles croissants : [-pi + 2*pi*n ; 2*pi*n]
- 10. Intervalles décroissants :
- 11. Points minimum : pi+2*pi*n
- 12. Fonction minimale : -1
- 13. Points maximum : 2*pi*n
- 14. Fonction maximale : 1
Propriétés de la tangente
.jpg)
- 1. Zone de définition : (-pi/2 +pi*n ; pi/2 +pi*n)
- 3. Fonction étrange.
- 5. Coordonnées des points d'intersection du graphe de fonctions avec l'axe Ox : (pi*n; 0)
- 6. Coordonnées des points d'intersection du graphe de fonction avec l'axe Oy : (0;0)
- 9. La fonction augmente par intervalles (-pi/2 + pi*n; pi/2 + pi*n)
Propriétés de la cotangente
.jpg)
- 1. Domaine de définition : (pi*n; pi +pi*n)
- 2. Plage de valeurs : axe des nombres entier
- 3. Fonction étrange.
- 4. Plus petite période positive : pi
- 5. Coordonnées des points d'intersection du graphe de fonctions avec l'axe Ox : (pi/2 + pi*n; 0)
- 6. Coordonnées des points d'intersection du graphe de fonctions avec l'axe Oy : non
- 7. Intervalles sur lesquels la fonction est positive : (pi*n; pi/2 +pi*n)
- 8. Intervalles auxquels la fonction est négative : (-pi/2 +pi*n ; pi*n)
- 9. La fonction décroît par intervalles (pi*n; pi +pi*n)
- 10. Il n’y a pas de points maximum ni minimum.
La figure ci-dessous montre plusieurs cercles unitaires, qui indiquent les signes du sinus, du cosinus, de la tangente et de la cotangente dans différents quartiers de coordonnées.
Le sinus et le cosinus sont nés à l’origine de la nécessité de calculer des quantités dans des triangles rectangles. Il a été remarqué que si la mesure en degrés des angles dans un triangle rectangle n'est pas modifiée, alors le rapport hauteur/largeur, quelle que soit la variation de longueur de ces côtés, reste toujours le même.
C’est ainsi qu’ont été introduites les notions de sinus et de cosinus. Le sinus d'un angle aigu dans un triangle rectangle est le rapport du côté opposé à l'hypoténuse, et le cosinus est le rapport du côté adjacent à l'hypoténuse.
Théorèmes des cosinus et des sinus
Mais les cosinus et les sinus peuvent être utilisés pour bien plus que de simples triangles rectangles. Pour trouver la valeur d'un angle ou d'un côté obtus ou aigu d'un triangle, il suffit d'appliquer le théorème des cosinus et des sinus.
Le théorème du cosinus est assez simple : « Le carré d’un côté d’un triangle est égal à la somme des carrés des deux autres côtés moins le double du produit de ces côtés et le cosinus de l’angle qui les sépare. »
Il existe deux interprétations du théorème des sinus : petite et étendue. Selon la mineure : « Dans un triangle, les angles sont proportionnels aux côtés opposés. » Ce théorème est souvent élargi en raison de la propriété du cercle circonscrit d'un triangle : « Dans un triangle, les angles sont proportionnels aux côtés opposés, et leur rapport est égal au diamètre du cercle circonscrit. »
Dérivés
La dérivée est un outil mathématique qui montre la rapidité avec laquelle une fonction change par rapport à un changement dans son argument. Les dérivés sont utilisés en géométrie et dans un certain nombre de disciplines techniques.
Lorsque vous résolvez des problèmes, vous devez savoir valeurs du tableau dérivés fonctions trigonométriques: sinus et cosinus. La dérivée d'un sinus est un cosinus, et un cosinus est un sinus, mais avec un signe moins.
Application en mathématiques
Les sinus et les cosinus sont particulièrement souvent utilisés pour résoudre des triangles rectangles et des problèmes qui leur sont associés.
La commodité des sinus et des cosinus se reflète également dans la technologie. Les angles et les côtés étaient faciles à évaluer à l’aide des théorèmes du cosinus et du sinus, décomposant les formes et les objets complexes en triangles « simples ». Les ingénieurs qui s'occupent souvent des calculs de rapports d'aspect et de mesures de degrés ont consacré beaucoup de temps et d'efforts à calculer les cosinus et les sinus des angles non tabulaires.
Puis les tables de Bradis sont venues à la rescousse, contenant des milliers de valeurs de sinus, cosinus, tangentes et cotangentes différents angles. À l'époque soviétique, certains enseignants obligeaient leurs élèves à mémoriser des pages de tableaux de Bradis.
Radian- magnitude angulaire arcs, longueur égal au rayon ou 57,295779513° degrés.
Un degré (en géométrie) équivaut à 1/360ème de cercle ou 1/90ème d'angle droit.
π = 3,141592653589793238462… (valeur approximative de Pi).
Table des cosinus pour les angles : 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, 180°, 210°, 225°, 240°, 270°, 300°, 315°, 330°, 360°.
| Angle x (en degrés) | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Angle x (en radians) | 0 | π/6 | π/4 | π/3 | π/2 | 2 x π/3 | 3xπ/4 | 5 x π/6 | π | 7xπ/6 | 5 x π/4 | 4 x π/3 | 3 x π/2 | 5 x π/3 | 7xπ/4 | 11 x π/6 | 2 x π |
| parce que x | 1 | √3/2 (0,8660) | √2/2 (0,7071) | 1/2 (0,5) | 0 | -1/2 (-0,5) | -√2/2 (-0,7071) | -√3/2 (-0,8660) | -1 | -√3/2 (-0,8660) | -√2/2 (-0,7071) | -1/2 (-0,5) | 0 | 1/2 (0,5) | √2/2 (0,7071) | √3/2 (0,8660) | 1 |
Notes IMPORTANTES!
1. Si vous voyez du charabia au lieu de formules, videz votre cache. Comment faire cela dans votre navigateur est écrit ici :
2. Avant de commencer à lire l'article, faites attention à notre navigateur pour la plupart ressource utile Pour
Sinus, cosinus, tangente, cotangente
Les notions de sinus (), cosinus (), tangente (), cotangente () sont inextricablement liées à la notion d'angle. Afin de bien comprendre ces concepts, à première vue complexes (qui provoquent un état d'horreur chez de nombreux écoliers), et pour s'assurer que « le diable n'est pas aussi terrible qu'on le peint », commençons par le tout début et comprendre le concept d’angle.
Notion d'angle : radian, degré
Regardons la photo. Le vecteur a « tourné » par rapport au point d’un certain montant. Donc la mesure de cette rotation par rapport à la position initiale sera coin.
Que devez-vous savoir d’autre sur le concept d’angle ? Et bien sûr, les unités d'angle !
L'angle, tant en géométrie qu'en trigonométrie, peut être mesuré en degrés et en radians.
Un angle de (un degré) est appelé angle central dans un cercle, basé sur un arc de cercle égal à une partie du cercle. Ainsi, le cercle entier est constitué de « morceaux » d’arcs de cercle, ou l’angle décrit par le cercle est égal.

Autrement dit, la figure ci-dessus montre un angle égal à, c'est-à-dire que cet angle repose sur un arc de cercle de la taille de la circonférence.
Un angle en radians est l'angle au centre d'un cercle sous-tendu par un arc de cercle dont la longueur est égale au rayon du cercle. Eh bien, avez-vous compris ? Sinon, comprenons-le à partir du dessin.

Ainsi, la figure montre un angle égal à un radian, c'est-à-dire que cet angle repose sur un arc de cercle dont la longueur est égale au rayon du cercle (la longueur est égale à la longueur ou au rayon égal à la longueur arcs). Ainsi, la longueur de l'arc est calculée par la formule :
Où est l’angle central en radians.
Eh bien, sachant cela, pouvez-vous répondre combien de radians sont contenus dans l’angle décrit par le cercle ? Oui, pour cela, vous devez vous rappeler la formule de la circonférence. Elle est là:
Eh bien, corrélons maintenant ces deux formules et constatons que l’angle décrit par le cercle est égal. Autrement dit, en corrélant la valeur en degrés et en radians, nous obtenons cela. Respectivement, . Comme vous pouvez le constater, contrairement à « degrés », le mot « radian » est omis, car l'unité de mesure ressort généralement clairement du contexte.
Combien y a-t-il de radians ? C'est exact!
J'ai compris? Alors allez-y et corrigez-le :
Vous rencontrez des difficultés ? Alors regarde réponses:
Triangle rectangle : sinus, cosinus, tangente, cotangente d'un angle
Nous avons donc compris le concept d'angle. Mais qu’est-ce que le sinus, le cosinus, la tangente et la cotangente d’un angle ? Voyons cela. Pour ce faire, un triangle rectangle nous aidera.

Comment s’appellent les côtés d’un triangle rectangle ? C'est vrai, l'hypoténuse et les jambes : l'hypoténuse est le côté qui se trouve à l'opposé de l'angle droit (dans notre exemple c'est le côté) ; les jambes sont les deux côtés restants et (ceux adjacents à angle droit), et, si l'on considère les jambes par rapport à l'angle, alors la jambe est la jambe adjacente et la jambe est l'opposée. Alors maintenant, répondons à la question : que sont le sinus, le cosinus, la tangente et la cotangente d’un angle ?
Sinus d'angle- c'est le rapport de la jambe opposée (éloignée) à l'hypoténuse.
Dans notre triangle.
Cosinus de l'angle- c'est le rapport entre la jambe adjacente (fermée) et l'hypoténuse.
Dans notre triangle.
Tangente de l'angle- c'est le rapport du côté opposé (éloigné) au côté adjacent (proche).
Dans notre triangle.
Cotangente d'angle- c'est le rapport entre la jambe adjacente (proche) et la jambe opposée (éloignée).
Dans notre triangle.
Ces définitions sont nécessaires souviens-toi! Pour qu'il soit plus facile de se rappeler quelle jambe diviser en quoi, vous devez clairement comprendre que dans tangente Et cotangente seules les jambes sont assises et l'hypoténuse n'apparaît que dans sinus Et cosinus. Et puis vous pouvez créer une chaîne d’associations. Par exemple, celui-ci :
Cosinus → toucher → toucher → adjacent ;
Cotangente → toucher → toucher → adjacent.
Tout d'abord, vous devez vous rappeler que le sinus, le cosinus, la tangente et la cotangente, comme les rapports des côtés d'un triangle, ne dépendent pas des longueurs de ces côtés (au même angle). Ne crois pas? Assurez-vous ensuite en regardant la photo :

Prenons par exemple le cosinus d’un angle. Par définition, à partir d'un triangle : , mais on peut calculer le cosinus d'un angle à partir d'un triangle : . Vous voyez, les longueurs des côtés sont différentes, mais la valeur du cosinus d'un angle est la même. Ainsi, les valeurs du sinus, du cosinus, de la tangente et de la cotangente dépendent uniquement de la grandeur de l'angle.
Si vous comprenez les définitions, alors allez-y et consolidez-les !
Pour le triangle représenté dans la figure ci-dessous, nous trouvons.

Eh bien, tu l'as eu ? Alors essayez-le vous-même : calculez la même chose pour l’angle.
Cercle unitaire (trigonométrique)
Comprenant les notions de degrés et de radians, nous avons considéré un cercle de rayon égal à. Un tel cercle s'appelle célibataire. Ce sera très utile lors de l’étude de la trigonométrie. Par conséquent, regardons-le un peu plus en détail.

Comme vous pouvez le voir, ce cercle est construit dans le système de coordonnées cartésiennes. Le rayon du cercle est égal à un, tandis que le centre du cercle se trouve à l'origine des coordonnées, la position initiale du rayon vecteur est fixée le long de la direction positive de l'axe (dans notre exemple, il s'agit du rayon).
Chaque point du cercle correspond à deux nombres : la coordonnée de l'axe et la coordonnée de l'axe. Quels sont ces numéros de coordonnées ? Et de manière générale, qu’ont-ils à voir avec le sujet abordé ? Pour ce faire, nous devons nous souvenir du triangle rectangle considéré. Dans la figure ci-dessus, vous pouvez voir deux triangles rectangles entiers. Considérons un triangle. Il est rectangulaire car perpendiculaire à l’axe.
A quoi est égal le triangle ? C'est exact. De plus, nous savons qu’il s’agit du rayon du cercle unité, ce qui signifie . Remplaçons cette valeur dans notre formule du cosinus. Voici ce qui se passe :
A quoi est égal le triangle ? Oui bien sur, ! Remplacez la valeur du rayon dans cette formule et obtenez :
Alors, pouvez-vous dire quelles sont les coordonnées du point, appartenant à un cercle? Eh bien, pas question ? Et si vous vous rendiez compte de cela et que vous n’étiez que des chiffres ? A quelle coordonnée correspond-il ? Et bien sûr, les coordonnées ! Et à quelle coordonnée correspond-elle ? C'est vrai, les coordonnées ! Donc point final.

À quoi valent donc et sont égaux ? C'est vrai, utilisons les définitions correspondantes de tangente et de cotangente et obtenons cela, a.
Et si l'angle est plus grand ? Par exemple, comme sur cette photo :

Qu'est-ce qui a changé dans cet exemple ? Voyons cela. Pour ce faire, revenons à un triangle rectangle. Considérons un triangle rectangle : angle (comme adjacent à un angle). Quelles sont les valeurs du sinus, du cosinus, de la tangente et de la cotangente pour un angle ? C'est vrai, nous adhérons aux définitions correspondantes des fonctions trigonométriques :
Eh bien, comme vous pouvez le constater, la valeur du sinus de l'angle correspond toujours à la coordonnée ; la valeur du cosinus de l'angle - la coordonnée ; et les valeurs de tangente et de cotangente aux rapports correspondants. Ainsi, ces relations s’appliquent à toute rotation du rayon vecteur.
Il a déjà été mentionné que la position initiale du rayon vecteur se situe dans la direction positive de l’axe. Jusqu’à présent, nous avons fait pivoter ce vecteur dans le sens inverse des aiguilles d’une montre, mais que se passe-t-il si nous le faisons pivoter dans le sens des aiguilles d’une montre ? Rien d'extraordinaire, vous obtiendrez aussi un angle d'une certaine valeur, mais seulement il sera négatif. Ainsi, en faisant tourner le rayon vecteur dans le sens inverse des aiguilles d'une montre, nous obtenons angles positifs, et en tournant dans le sens des aiguilles d'une montre - négatif.
Ainsi, nous savons qu’une révolution entière du rayon vecteur autour d’un cercle est ou. Est-il possible de faire pivoter le rayon vecteur vers ou vers ? Bien sûr que tu peux! Dans le premier cas, le rayon vecteur fera donc un tour complet et s'arrêtera en position ou.
Dans le deuxième cas, c'est-à-dire que le rayon vecteur fera trois tours complets et s'arrêtera en position ou.
Ainsi, à partir des exemples ci-dessus, nous pouvons conclure que les angles qui diffèrent par ou (où est un nombre entier) correspondent à la même position du rayon vecteur.
La figure ci-dessous montre un angle. La même image correspond au coin, etc. Cette liste peut être poursuivie indéfiniment. Tous ces angles peuvent être écrits par la formule générale ou (où est un nombre entier)

Maintenant, connaissant les définitions des fonctions trigonométriques de base et en utilisant le cercle unité, essayez de répondre quelles sont les valeurs :
Voici un cercle unitaire pour vous aider :

Vous rencontrez des difficultés ? Alors découvrons-le. Nous savons donc que :
A partir de là, on détermine les coordonnées des points correspondant à certaines mesures d'angle. Bon, commençons dans l'ordre : l'angle à correspond à un point avec des coordonnées, donc :
N'existe pas;
De plus, en adhérant à la même logique, nous découvrons que les coins correspondent respectivement à des points avec des coordonnées. Sachant cela, il est facile de déterminer les valeurs des fonctions trigonométriques aux points correspondants. Essayez-le vous-même d'abord, puis vérifiez les réponses.
Réponses:
Ainsi, nous pouvons faire le tableau suivant :

Il n’est pas nécessaire de mémoriser toutes ces valeurs. Il suffit de rappeler la correspondance entre les coordonnées des points sur le cercle unité et les valeurs des fonctions trigonométriques :
Mais les valeurs des fonctions trigonométriques des angles dans et, données dans le tableau ci-dessous, il faut se souvenir:

N'ayez pas peur, nous allons maintenant vous montrer un exemple assez simple pour retenir les valeurs correspondantes:
Pour utiliser cette méthode, il est essentiel de mémoriser les valeurs du sinus pour les trois mesures d'angle (), ainsi que la valeur de la tangente de l'angle. Connaissant ces valeurs, il est assez simple de restituer l'intégralité du tableau - les valeurs du cosinus sont transférées conformément aux flèches, soit :
Sachant cela, vous pouvez restaurer les valeurs de. Le numérateur " " correspondra et le dénominateur " " correspondra. Les valeurs cotangentes sont transférées conformément aux flèches indiquées sur la figure. Si vous comprenez cela et que vous vous souvenez du diagramme avec les flèches, il suffira alors de mémoriser toutes les valeurs du tableau.
Coordonnées d'un point sur un cercle
Est-il possible de trouver un point (ses coordonnées) sur un cercle, connaître les coordonnées du centre du cercle, son rayon et son angle de rotation?
Bien sûr que tu peux! Sortons-le formule générale trouver les coordonnées d'un point.
Par exemple, voici un cercle devant nous :

On nous dit que le point est le centre du cercle. Le rayon du cercle est égal. Il faut trouver les coordonnées d'un point obtenues en faisant pivoter le point de degrés.
Comme le montre la figure, la coordonnée du point correspond à la longueur du segment. La longueur du segment correspond à la coordonnée du centre du cercle, c'est-à-dire qu'elle est égale. La longueur d'un segment peut être exprimée en utilisant la définition du cosinus :
Ensuite, nous avons cela pour la coordonnée du point.
En utilisant la même logique, nous trouvons la valeur de coordonnée y du point. Ainsi,
Alors, dans vue générale les coordonnées des points sont déterminées par les formules :
Coordonnées du centre du cercle,
Rayon du cercle,
L'angle de rotation du rayon vectoriel.
Comme vous pouvez le constater, pour le cercle unité que nous considérons, ces formules sont considérablement réduites, puisque les coordonnées du centre sont égales à zéro et le rayon est égal à un :
Eh bien, essayons ces formules en nous entraînant à trouver des points sur un cercle ?
1. Trouvez les coordonnées d'un point sur le cercle unité obtenu en faisant pivoter le point.
2. Trouvez les coordonnées d'un point sur le cercle unité obtenu en faisant pivoter le point.
3. Trouvez les coordonnées d'un point sur le cercle unité obtenu en faisant pivoter le point.
4. Le point est le centre du cercle. Le rayon du cercle est égal. Il faut retrouver les coordonnées du point obtenu en faisant tourner le rayon vecteur initial de.
5. Le point est le centre du cercle. Le rayon du cercle est égal. Il faut retrouver les coordonnées du point obtenu en faisant tourner le rayon vecteur initial de.
Vous avez du mal à trouver les coordonnées d'un point sur un cercle ?
Résolvez ces cinq exemples (ou apprenez à les résoudre) et vous apprendrez à les trouver !
RÉSUMÉ ET FORMULES DE BASE
Le sinus d'un angle est le rapport entre la jambe opposée (lointaine) et l'hypoténuse.
Le cosinus d'un angle est le rapport entre la jambe adjacente (fermée) et l'hypoténuse.
La tangente d'un angle est le rapport entre le côté opposé (éloigné) et le côté adjacent (proche).
La cotangente d'un angle est le rapport entre le côté adjacent (proche) et le côté opposé (éloigné).
Eh bien, le sujet est terminé. Si vous lisez ces lignes, c’est que vous êtes très cool.
Parce que seulement 5 % des gens sont capables de maîtriser quelque chose par eux-mêmes. Et si vous lisez jusqu'au bout, alors vous êtes dans ces 5% !
Maintenant, le plus important.
Vous avez compris la théorie sur ce sujet. Et je le répète, ça... c'est juste super ! Vous êtes déjà meilleur que la grande majorité de vos pairs.
Le problème est que cela ne suffit peut-être pas...
Pour quoi?
Pour réussite Examen d'État unifié, pour l'admission à l'université avec un budget limité et, SURTOUT, à vie.
Je ne vais vous convaincre de rien, je dirai juste une chose...
Les personnes qui ont reçu une bonne éducation, gagnent bien plus que ceux qui ne l’ont pas reçu. Ce sont des statistiques.
Mais ce n’est pas l’essentiel.
L'essentiel est qu'ils soient PLUS HEUREUX (il existe de telles études). Peut-être parce qu'il y a beaucoup plus d'ouverture devant eux plus de possibilités et la vie devient plus lumineuse ? Je ne sais pas...
Mais pensez par vous-même...
Que faut-il pour être sûr d'être meilleur que les autres à l'examen d'État unifié et finalement être... plus heureux ?
GAGNEZ VOTRE MAIN EN RÉSOUDANT DES PROBLÈMES SUR CE SUJET.
Aucune théorie ne vous sera demandée lors de l'examen.
Tu auras besoin de résoudre des problèmes contre le temps.
Et si vous ne les avez pas résolus (BEAUCOUP !), vous ferez certainement une erreur stupide quelque part ou vous n’aurez tout simplement pas le temps.
C'est comme dans le sport : il faut répéter plusieurs fois pour gagner avec certitude.
Retrouvez la collection où vous voulez, nécessairement avec des solutions, analyse détaillée et décidez, décidez, décidez !
Vous pouvez utiliser nos tâches (facultatif) et nous les recommandons bien sûr.
Afin de mieux utiliser nos tâches, vous devez contribuer à prolonger la durée de vie du manuel YouClever que vous lisez actuellement.
Comment? Il existe deux options :
- Débloquez toutes les tâches cachées dans cet article -
- Débloquez l'accès à toutes les tâches cachées dans les 99 articles du manuel - Acheter un manuel - 499 RUR
Oui, nous avons 99 articles de ce type dans notre manuel et l'accès à toutes les tâches et à tous les textes cachés qu'elles contiennent peut être ouvert immédiatement.
L'accès à toutes les tâches cachées est assuré pendant TOUTE la vie du site.
En conclusion...
Si vous n'aimez pas nos tâches, trouvez-en d'autres. Ne vous arrêtez pas à la théorie.
« Compris » et « Je peux résoudre » sont des compétences complètement différentes. Vous avez besoin des deux.
Trouvez les problèmes et résolvez-les !
La trigonométrie, en tant que science, est originaire de l'Orient ancien. D'abord rapports trigonométriques ont été développés par des astronomes pour créer un calendrier précis et naviguer selon les étoiles. Ces calculs concernaient la trigonométrie sphérique, alors qu'en cours scolaireétudier les rapports des côtés et des angles d’un triangle plan.
La trigonométrie est une branche des mathématiques qui traite des propriétés des fonctions trigonométriques et des relations entre les côtés et les angles des triangles.
À l'apogée de la culture et de la science, au 1er millénaire après J.-C., les connaissances se sont propagées de Orient ancienà la Grèce. Mais les principales découvertes de la trigonométrie sont le mérite des hommes du Califat arabe. En particulier, le scientifique turkmène al-Marazwi a introduit des fonctions telles que la tangente et la cotangente et a compilé les premiers tableaux de valeurs pour les sinus, les tangentes et les cotangentes. Les concepts de sinus et de cosinus ont été introduits par des scientifiques indiens. La trigonométrie a reçu beaucoup d'attention dans les œuvres de grandes figures de l'Antiquité comme Euclide, Archimède et Ératosthène.
Grandeurs de base de la trigonométrie
Fonctions trigonométriques de base argument numérique– ce sont le sinus, le cosinus, la tangente et la cotangente. Chacun d'eux a son propre graphe : sinus, cosinus, tangente et cotangente.
Les formules de calcul des valeurs de ces grandeurs sont basées sur le théorème de Pythagore. Il est mieux connu des écoliers dans la formulation : « Pantalon pythagoricien, égal dans toutes les directions », puisque la preuve est donnée à l'aide de l'exemple d'un triangle rectangle isocèle.
Le sinus, le cosinus et d'autres dépendances établissent la relation entre coins pointus et les côtés de n'importe quel triangle rectangle. Présentons les formules de calcul de ces quantités pour l'angle A et traçons les relations entre les fonctions trigonométriques :

Comme vous pouvez le voir, tg et ctg sont fonctions inverses. Si nous imaginons la jambe a comme le produit du sin A et de l'hypoténuse c, et la jambe b comme cos A * c, nous obtenons les formules suivantes pour la tangente et la cotangente :

Cercle trigonométrique
Graphiquement, la relation entre les quantités mentionnées peut être représentée comme suit :

Circonférence, en dans ce cas, représente toutes les valeurs possibles de l'angle α - de 0° à 360°. Comme le montre la figure, chaque fonction prend une valeur négative ou positive selon l'angle. Par exemple, sin α aura le signe « + » si α appartient aux 1er et 2ème quarts du cercle, c'est-à-dire qu'il est compris entre 0° et 180°. Pour α de 180° à 360° (quarts III et IV), sin α ne peut être qu'une valeur négative.
Essayons de construire tables trigonométriques pour des angles spécifiques et découvrez la valeur des quantités.

Les valeurs de α égales à 30°, 45°, 60°, 90°, 180° etc. sont appelées cas particuliers. Les valeurs des fonctions trigonométriques correspondantes sont calculées et présentées sous forme de tableaux spéciaux.

Ces angles n'ont pas été choisis au hasard. La désignation π dans les tableaux correspond aux radians. Rad est l'angle auquel la longueur d'un arc de cercle correspond à son rayon. Cette valeur a été introduite afin d'établir une dépendance universelle ; lors du calcul en radians, la longueur réelle du rayon en cm n'a pas d'importance.

Les angles dans les tableaux des fonctions trigonométriques correspondent aux valeurs en radians :

Il n’est donc pas difficile de deviner que 2π est un cercle complet ou 360°.
Propriétés des fonctions trigonométriques : sinus et cosinus
Afin de considérer et de comparer les propriétés fondamentales du sinus et du cosinus, de la tangente et de la cotangente, il est nécessaire de dessiner leurs fonctions. Cela peut être réalisé sous la forme d'une courbe située dans un système de coordonnées bidimensionnel.
Considérer tableau de comparaison propriétés du sinus et du cosinus :

| Onde sinusoïdale | Cosinus |
|---|---|
| y = péché x | y = cos x |
| ODZ[-1 ; 1] | ODZ[-1 ; 1] |
| sin x = 0, pour x = πk, où k ϵ Z | cos x = 0, pour x = π/2 + πk, où k ϵ Z |
| sin x = 1, pour x = π/2 + 2πk, où k ϵ Z | cos x = 1, à x = 2πk, où k ϵ Z |
| sin x = - 1, à x = 3π/2 + 2πk, où k ϵ Z | cos x = - 1, pour x = π + 2πk, où k ϵ Z |
| sin (-x) = - sin x, c'est-à-dire que la fonction est impaire | cos (-x) = cos x, c'est-à-dire que la fonction est paire |
| la fonction est périodique, la plus petite période est 2π | |
| sin x › 0, avec x appartenant au 1er et au 2ème quartiers ou de 0° à 180° (2πk, π + 2πk) | cos x › 0, avec x appartenant aux quartiers I et IV ou de 270° à 90° (- π/2 + 2πk, π/2 + 2πk) |
| sin x ‹ 0, avec x appartenant aux troisième et quatrième quartiers ou de 180° à 360° (π + 2πk, 2π + 2πk) | cos x ‹ 0, avec x appartenant aux 2ème et 3ème quartiers ou de 90° à 270° (π/2 + 2πk, 3π/2 + 2πk) |
| augmente dans l'intervalle [- π/2 + 2πk, π/2 + 2πk] | augmente sur l'intervalle [-π + 2πk, 2πk] |
| diminue sur les intervalles [π/2 + 2πk, 3π/2 + 2πk] | diminue à intervalles réguliers |
| dérivée (sin x)’ = cos x | dérivée (cos x)’ = - sin x |
Déterminer si une fonction est paire ou non est très simple. Il suffit d'imaginer un cercle trigonométrique avec les signes des grandeurs trigonométriques et de « plier » mentalement le graphique par rapport à l'axe OX. Si les signes coïncident, la fonction est paire, sinon elle est impaire.

L’introduction des radians et l’énumération des propriétés fondamentales des ondes sinusoïdales et cosinusoïdales nous permettent de présenter le schéma suivant :

Il est très simple de vérifier que la formule est correcte. Par exemple, pour x = π/2, le sinus est 1, tout comme le cosinus de x = 0. La vérification peut être effectuée en consultant des tableaux ou en traçant des courbes de fonctions pour des valeurs données.
Propriétés des tangentsoïdes et des cotangentsoïdes
Les graphiques des fonctions tangente et cotangente diffèrent considérablement des fonctions sinus et cosinus. Les valeurs tg et ctg sont réciproques l'une de l'autre.


- Y = bronzage x.
- La tangente tend vers les valeurs de y en x = π/2 + πk, mais ne les atteint jamais.
- La plus petite période positive de la tangentoïde est π.
- Tg (- x) = - tg x, c'est-à-dire que la fonction est impaire.
- Tg x = 0, pour x = πk.
- La fonction augmente.
- Tg x › 0, pour x ϵ (πk, π/2 + πk).
- Tg x ‹ 0, pour x ϵ (— π/2 + πk, πk).
- Dérivée (tg x)' = 1/cos 2 x.
Considérons image graphique cotangentoïdes ci-dessous dans le texte.

Principales propriétés des cotangentoïdes :
- Y = lit bébé x.
- Contrairement aux fonctions sinus et cosinus, dans la tangentoïde Y peut prendre les valeurs de l'ensemble de tous les nombres réels.
- Le cotangentoïde tend vers les valeurs de y en x = πk, mais ne les atteint jamais.
- La plus petite période positive d'un cotangentoïde est π.
- Ctg (- x) = - ctg x, c'est-à-dire que la fonction est impaire.
- Ctg x = 0, pour x = π/2 + πk.
- La fonction est décroissante.
- Ctg x › 0, pour x ϵ (πk, π/2 + πk).
- Ctg x ‹ 0, pour x ϵ (π/2 + πk, πk).
- Dérivée (ctg x)’ = - 1/sin 2 x Correct