La suma de logaritmos con la misma base. Identidad logarítmica básica. Sustitución de límites de integración
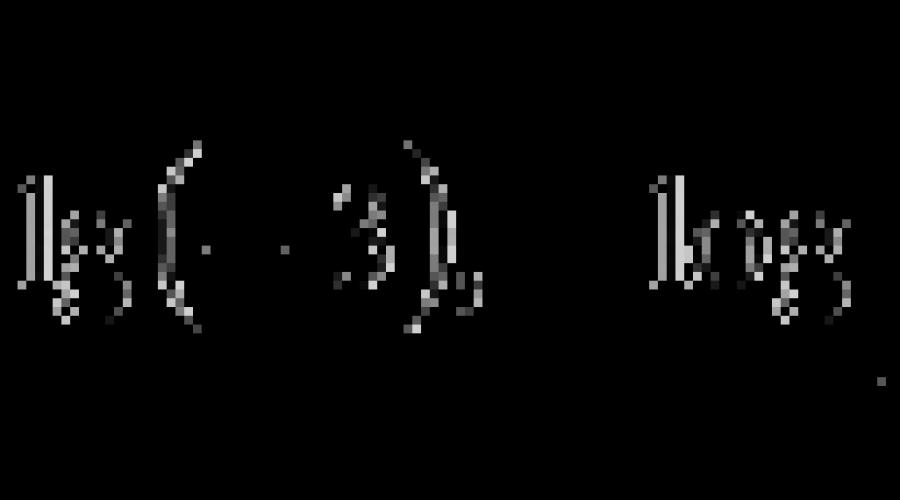
El enfoque de este artículo es logaritmo. Aquí daremos una definición de logaritmo, mostraremos la notación aceptada, daremos ejemplos de logaritmos y hablaremos sobre logaritmos naturales y decimales. Después de eso, veamos los principales. identidad logarítmica.
Navegación de páginas.
Definición de logaritmo
El concepto de logaritmo surge al resolver un problema en en cierto sentido inversa, cuando necesitas encontrar el exponente de valor conocido grado y base conocida.
Pero basta de prefacios, es hora de responder a la pregunta “¿qué es un logaritmo”? Demos la definición correspondiente.
Definición.
Logaritmo de b en base a, donde a>0, a≠1 y b>0 es el exponente al que necesitas elevar el número a para obtener b como resultado.
En esta etapa, observamos que la palabra hablada "logaritmo" debería plantear inmediatamente dos preguntas de seguimiento: "qué número" y "sobre qué base". En otras palabras, simplemente no existe logaritmo, sino sólo el logaritmo de un número con respecto a alguna base.
Entremos ahora mismo notación logarítmica: El logaritmo de un número b en base a generalmente se denota como log a b. El logaritmo de un número b en base e y el logaritmo en base 10 tienen sus propias designaciones especiales lnb y logb, respectivamente, es decir, no escriben log e b, sino lnb, y no log 10 b, sino lgb.
Ahora podemos dar: .
y los registros  No tiene sentido, ya que en el primero de ellos hay un número negativo bajo el signo de logaritmo, en el segundo hay un número negativo en la base, y en el tercero hay un número negativo bajo el signo de logaritmo y una unidad en la base.
No tiene sentido, ya que en el primero de ellos hay un número negativo bajo el signo de logaritmo, en el segundo hay un número negativo en la base, y en el tercero hay un número negativo bajo el signo de logaritmo y una unidad en la base.
Ahora hablemos de reglas para leer logaritmos. La notación log a b se lee como "el logaritmo de b en base a". Por ejemplo, log 2 3 es el logaritmo de tres en base 2 y es el logaritmo de dos punto dos tercios en base 2. raíz cuadrada de cinco. El logaritmo en base e se llama logaritmo natural, y la notación lnb dice "logaritmo natural de b". Por ejemplo, ln7 es el logaritmo natural de siete y lo leeremos como el logaritmo natural de pi. El logaritmo en base 10 también tiene un nombre especial: logaritmo decimal, y lgb se lee como "logaritmo decimal de b". Por ejemplo, lg1 es el logaritmo decimal de uno y lg2.75 es el logaritmo decimal de dos coma siete cinco centésimas.
Vale la pena detenerse por separado en las condiciones a>0, a≠1 y b>0, bajo las cuales se da la definición del logaritmo. Expliquemos de dónde vienen estas restricciones. Una igualdad de la forma llamada , que se deriva directamente de la definición de logaritmo dada anteriormente, nos ayudará a lograr esto.
Empecemos con a≠1. Dado que uno elevado a cualquier potencia es igual a uno, la igualdad sólo puede ser verdadera cuando b=1, pero log 1 1 puede ser cualquier número real. Para evitar esta ambigüedad, se supone a≠1.
Justifiquemos la conveniencia de la condición a>0. Con a=0, según la definición de logaritmo, tendríamos una igualdad que sólo es posible con b=0. Pero entonces log 0 0 puede ser cualquier número real distinto de cero, ya que cero elevado a cualquier potencia distinta de cero es cero. La condición a≠0 nos permite evitar esta ambigüedad. Y cuando un<0 нам бы пришлось отказаться от рассмотрения рациональных и иррациональных значений логарифма, так как степень с рациональным и ирindicador racional definido sólo para bases no negativas. Por tanto, se acepta la condición a>0.
Finalmente, la condición b>0 se deriva de la desigualdad a>0, ya que , y el valor de una potencia con base positiva a es siempre positivo.
Para concluir este punto, digamos que la definición dada de logaritmo le permite indicar inmediatamente el valor del logaritmo cuando el número bajo el signo del logaritmo es una determinada potencia de la base. En efecto, la definición de logaritmo nos permite afirmar que si b=a p, entonces el logaritmo del número b en base a es igual a p. Es decir, la igualdad log a a p =p es verdadera. Por ejemplo, sabemos que 2 3 =8, entonces log 2 8=3. Hablaremos más sobre esto en el artículo.
Los logaritmos, como cualquier número, se pueden sumar, restar y transformar de todas las formas posibles. Pero como los logaritmos no son exactamente numeros regulares, aquí hay reglas, que se llaman propiedades principales.
Definitivamente necesitas conocer estas reglas; sin ellas, no se puede resolver ni un solo problema logarítmico grave. Además, hay muy pocos: puedes aprender todo en un día. Así que comencemos.
Sumar y restar logaritmos
Considere dos logaritmos con las mismas bases: log a incógnita y registrar a y. Luego se pueden sumar y restar, y:
- registro a incógnita+ iniciar sesión a y= iniciar sesión a (incógnita · y);
- registro a incógnita− iniciar sesión a y= iniciar sesión a (incógnita : y).
Entonces, la suma de logaritmos es igual al logaritmo del producto y la diferencia es igual al logaritmo del cociente. Tenga en cuenta: punto clave Aquí - motivos idénticos. Si los motivos son diferentes, ¡estas reglas no funcionan!
Estas fórmulas te ayudarán a calcular una expresión logarítmica incluso cuando no se consideran sus partes individuales (consulta la lección “¿Qué es un logaritmo”). Eche un vistazo a los ejemplos y vea:
Registro 6 4 + registro 6 9.
Como los logaritmos tienen las mismas bases, usamos la fórmula de suma:
registro 6 4 + registro 6 9 = registro 6 (4 9) = registro 6 36 = 2.
Tarea. Encuentra el valor de la expresión: log 2 48 − log 2 3.
Las bases son las mismas, utilizamos la fórmula de diferencia:
registro 2 48 − registro 2 3 = registro 2 (48: 3) = registro 2 16 = 4.
Tarea. Encuentra el valor de la expresión: log 3 135 − log 3 5.
Nuevamente las bases son las mismas, entonces tenemos:
registro 3 135 − registro 3 5 = registro 3 (135: 5) = registro 3 27 = 3.
Como puedes ver, las expresiones originales se componen de logaritmos "malos", que no se calculan por separado. Pero después de las transformaciones se obtienen números completamente normales. Muchos se basan en este hecho. pruebas. Sí, en el Examen Estatal Unificado se ofrecen expresiones tipo test con toda seriedad (a veces prácticamente sin cambios).
Extrayendo el exponente del logaritmo
Ahora compliquemos un poco la tarea. ¿Qué pasa si la base o argumento de un logaritmo es una potencia? Entonces el exponente de este grado se puede sacar del signo del logaritmo según las siguientes reglas:
Es fácil notar que última regla sigue a los dos primeros. Pero es mejor recordarlo de todos modos; en algunos casos, esto reducirá significativamente la cantidad de cálculos.
Por supuesto, todas estas reglas tienen sentido si se observa la ODZ del logaritmo: a > 0, a ≠ 1, incógnita> 0. Y una cosa más: aprende a aplicar todas las fórmulas no sólo de izquierda a derecha, sino también al revés, es decir. Puede ingresar los números antes del signo del logaritmo en el propio logaritmo. Esto es lo que más a menudo se requiere.
Tarea. Encuentra el valor de la expresión: log 7 49 6 .
Eliminemos el grado en el argumento usando la primera fórmula:
registro 7 49 6 = 6 registro 7 49 = 6 2 = 12
Tarea. Encuentra el significado de la expresión:
[Título de la imagen]
Tenga en cuenta que el denominador contiene un logaritmo, cuya base y argumento son potencias exactas: 16 = 2 4; 49 = 7 2. Tenemos:
 [Título de la imagen]
[Título de la imagen] Creo que el último ejemplo requiere alguna aclaración. ¿A dónde se han ido los logaritmos? Hasta el último momento trabajamos sólo con el denominador. Presentamos la base y el argumento del logaritmo allí en forma de potencias y eliminamos los exponentes: obtuvimos una fracción de "tres pisos".
Ahora veamos la fracción principal. El numerador y el denominador contienen el mismo número: log 2 7. Como log 2 7 ≠ 0, podemos reducir la fracción: 2/4 permanecerá en el denominador. Según las reglas de la aritmética, el cuatro se puede trasladar al numerador, que es lo que se hizo. El resultado fue la respuesta: 2.
Transición a una nueva fundación.
Hablando de las reglas para sumar y restar logaritmos, enfaticé específicamente que solo funcionan con las mismas bases. ¿Qué pasa si las razones son diferentes? ¿Qué pasa si no son potencias exactas del mismo número?
Las fórmulas para la transición a una nueva base vienen al rescate. Formulémoslos en forma de teorema:
Sea el registro del logaritmo a incógnita. Entonces para cualquier número do tal que do> 0 y do≠ 1, la igualdad es verdadera:
[Título de la imagen]
En particular, si ponemos do = incógnita, obtenemos:
[Título de la imagen]
De la segunda fórmula se deduce que la base y el argumento del logaritmo se pueden intercambiar, pero en este caso se “da la vuelta” a toda la expresión, es decir el logaritmo aparece en el denominador.
Estas fórmulas rara vez se encuentran en expresiones numéricas ordinarias. Es posible evaluar qué tan convenientes son solo al resolver ecuaciones y desigualdades logarítmicas.
Sin embargo, hay problemas que no pueden resolverse en absoluto excepto trasladándose a una nueva fundación. Veamos un par de estos:
Tarea. Encuentra el valor de la expresión: log 5 16 log 2 25.
Tenga en cuenta que los argumentos de ambos logaritmos contienen potencias exactas. Saquemos los indicadores: log 5 16 = log 5 2 4 = 4log 5 2; registro 2 25 = registro 2 5 2 = 2 registro 2 5;
Ahora “invirtamos” el segundo logaritmo:
[Título de la imagen]Como el producto no cambia al reorganizar los factores, multiplicamos tranquilamente cuatro por dos y luego nos ocupamos de los logaritmos.
Tarea. Encuentra el valor de la expresión: log 9 100 lg 3.
La base y el argumento del primer logaritmo son potencias exactas. Anotemos esto y eliminemos los indicadores:
[Título de la imagen]Ahora eliminemos el logaritmo decimal moviéndolo a una nueva base:
[Título de la imagen]Identidad logarítmica básica
A menudo, en el proceso de solución es necesario representar un número como un logaritmo con una base determinada. En este caso nos ayudarán las siguientes fórmulas:
En el primer caso, el número norte se convierte en un indicador del grado que ocupa el argumento. Número norte puede ser absolutamente cualquier cosa, porque es solo un valor logarítmico.
La segunda fórmula es en realidad una definición parafraseada. Así se llama: la identidad logarítmica básica.
De hecho, ¿qué pasará si el número b elevar a tal potencia que el número b a esta potencia se le da el número a? Así es: obtienes este mismo número a. Lea este párrafo con atención nuevamente; muchas personas se quedan estancadas en él.
Al igual que las fórmulas para pasar a una nueva base, la identidad logarítmica básica es a veces la única solución posible.
Tarea. Encuentra el significado de la expresión:
[Título de la imagen]
Tenga en cuenta que log 25 64 = log 5 8; simplemente tomamos el cuadrado de la base y el argumento del logaritmo. Teniendo en cuenta las reglas para multiplicar potencias con la misma base, obtenemos:
[Título de la imagen]Si alguien no lo sabe, esta fue una tarea real del Examen Estatal Unificado :)
Unidad logarítmica y cero logarítmico
En conclusión, daré dos identidades que difícilmente pueden llamarse propiedades; más bien, son consecuencias de la definición del logaritmo. Aparecen constantemente en los problemas y, sorprendentemente, crean problemas incluso para los estudiantes "avanzados".
- registro a a= 1 es una unidad logarítmica. Recuerda de una vez por todas: logaritmo en cualquier base a desde esta misma base es igual a uno.
- registro a 1 = 0 es cero logarítmico. Base a puede ser cualquier cosa, pero si el argumento contiene uno, ¡el logaritmo es igual a cero! Porque a 0 = 1 es una consecuencia directa de la definición.
Esas son todas las propiedades. ¡Asegúrate de practicar poniéndolos en práctica! Descargue la hoja de trucos al comienzo de la lección, imprímala y resuelva los problemas.
Como sabes, al multiplicar expresiones con potencias, sus exponentes siempre suman (a b *a c = a b+c). Este ley matemática fue deducida por Arquímedes, y más tarde, en el siglo VIII, el matemático Virasen creó una tabla de exponentes enteros. Fueron ellos quienes sirvieron para un mayor descubrimiento de los logaritmos. Se pueden encontrar ejemplos del uso de esta función en casi todos los lugares donde es necesario simplificar una multiplicación engorrosa mediante una simple suma. Si dedicas 10 minutos a leer este artículo, te explicaremos qué son los logaritmos y cómo trabajar con ellos. En un lenguaje sencillo y accesible.
Definición en matemáticas
Un logaritmo es una expresión de la siguiente forma: log a b=c, es decir, el logaritmo de cualquier número no negativo (es decir, cualquier positivo) “b” a su base “a” se considera la potencia “c ” a lo cual es necesario elevar la base “a” para finalmente obtener el valor “b”. Analicemos el logaritmo usando ejemplos, digamos que hay una expresión log 2 8. ¿Cómo encontrar la respuesta? Es muy simple, necesitas encontrar una potencia tal que de 2 a la potencia requerida obtengas 8. Después de hacer algunos cálculos mentales, ¡obtenemos el número 3! Y eso es cierto, porque 2 elevado a 3 da la respuesta 8.
Tipos de logaritmos
Para muchos alumnos y estudiantes, este tema parece complicado e incomprensible, pero en realidad los logaritmos no dan tanto miedo, lo principal es comprender su significado general y recordar sus propiedades y algunas reglas. hay tres especies individuales expresiones logarítmicas:
- Logaritmo natural en a, donde la base es el número de Euler (e = 2,7).
- Decimal a, donde la base es 10.
- Logaritmo de cualquier número b en base a>1.
Cada uno de ellos está decidido. de forma estándar, que incluye simplificación, reducción y posterior reducción a un logaritmo mediante teoremas logarítmicos. para recibir valores correctos logaritmos, debes recordar sus propiedades y la secuencia de acciones al resolverlos.
Reglas y algunas restricciones.
En matemáticas existen varias reglas-restricciones que se aceptan como axioma, es decir, no están sujetas a discusión y son la verdad. Por ejemplo, es imposible dividir números por cero y también es imposible extraer una raíz par de números negativos. Los logaritmos también tienen sus propias reglas, siguiendo las cuales puedes aprender fácilmente a trabajar incluso con expresiones logarítmicas largas y amplias:
- La base “a” siempre debe ser mayor que cero, y no igual a 1, de lo contrario la expresión perderá su significado, porque “1” y “0” en cualquier grado siempre son iguales a sus valores;
- si a > 0, entonces a b >0, resulta que “c” también debe ser mayor que cero.
¿Cómo resolver logaritmos?
Por ejemplo, la tarea es encontrar la respuesta a la ecuación 10 x = 100. Esto es muy fácil, debes elegir una potencia elevando el número diez a lo que obtenemos 100. Esto, por supuesto, es 10 2 = 100.
Ahora representemos esta expresión en forma logarítmica. Obtenemos log 10 · 100 = 2. Al resolver logaritmos, todas las acciones prácticamente convergen para encontrar la potencia a la que es necesario ingresar la base del logaritmo para obtener un número determinado.
Para determinar con precisión el valor de un grado desconocido, es necesario aprender a trabajar con una tabla de grados. Se parece a esto:

Como puedes ver, algunos exponentes se pueden adivinar intuitivamente si tienes una mente técnica y conocimientos de la tabla de multiplicar. Sin embargo para valores grandes Necesitarás una tabla de grados. Puede ser utilizado incluso por aquellos que no saben nada sobre temas matemáticos complejos. La columna de la izquierda contiene números (base a), la fila superior de números es el valor de la potencia c a la que se eleva el número a. En la intersección, las celdas contienen los valores numéricos que son la respuesta (a c =b). Tomemos, por ejemplo, la primera celda con el número 10 y la elevamos al cuadrado, obtenemos el valor 100, que se indica en la intersección de nuestras dos celdas. ¡Todo es tan simple y fácil que incluso el humanista más verdadero lo entenderá!
Ecuaciones y desigualdades
Resulta que bajo ciertas condiciones el exponente es el logaritmo. Por tanto, cualquier expresión numérica matemática se puede escribir como una igualdad logarítmica. Por ejemplo, 3 4 =81 se puede escribir como el logaritmo en base 3 de 81 igual a cuatro (log 3 81 = 4). Para potencias negativas las reglas son las mismas: 2 -5 = 1/32 lo escribimos como un logaritmo, obtenemos log 2 (1/32) = -5. Una de las secciones más fascinantes de las matemáticas es el tema de los "logaritmos". Veremos ejemplos y soluciones de ecuaciones a continuación, inmediatamente después de estudiar sus propiedades. Ahora veamos cómo son las desigualdades y cómo distinguirlas de las ecuaciones.

Dada una expresión de la siguiente forma: log 2 (x-1) > 3 - es desigualdad logarítmica, ya que el valor desconocido "x" está bajo el signo del logaritmo. Y también en la expresión se comparan dos cantidades: el logaritmo del número deseado en base dos es mayor que el número tres.
La diferencia más importante entre ecuaciones logarítmicas y desigualdades es que las ecuaciones con logaritmos (ejemplo: logaritmo 2 x = √9) implican uno o más valores numéricos específicos en la respuesta, mientras que al resolver desigualdades, se definen como una región. valores aceptables y los puntos de interrupción de esta función. Como consecuencia, la respuesta no es un simple conjunto de números individuales, como en la respuesta a una ecuación, sino una serie o conjunto continuo de números.

Teoremas básicos sobre logaritmos
Al resolver problemas primitivos de encontrar los valores de un logaritmo, es posible que no se conozcan sus propiedades. Sin embargo, cuando se trata de ecuaciones o desigualdades logarítmicas, en primer lugar, es necesario comprender claramente y aplicar en la práctica todas las propiedades básicas de los logaritmos. Veremos ejemplos de ecuaciones más adelante; primero veamos cada propiedad con más detalle.
- La identidad principal se ve así: a logaB =B. Se aplica sólo cuando a es mayor que 0, distinto de uno y B es mayor que cero.
- El logaritmo del producto se puede representar en la siguiente fórmula: log d (s 1 * s 2) = log d s 1 + log d s 2. En este caso, la condición obligatoria es: d, s 1 y s 2 > 0; a≠1. Puedes dar una prueba de esta fórmula logarítmica, con ejemplos y solución. Sean log a s 1 = f 1 y log a s 2 = f 2, luego a f1 = s 1, a f2 = s 2. Obtenemos que s 1 * s 2 = a f1 *a f2 = a f1+f2 (propiedades de grados), y luego por definición: log a (s 1 * s 2) = f 1 + f 2 = log a s1 + log a s 2, que es lo que había que demostrar.
- El logaritmo del cociente se ve así: log a (s 1/ s 2) = log a s 1 - log a s 2.
- El teorema en forma de fórmula adquiere siguiente vista: iniciar sesión a q b n = n/q iniciar sesión a b.
Esta fórmula se llama "propiedad del grado de logaritmo". Se parece a las propiedades de los grados ordinarios, y no es sorprendente, porque todas las matemáticas se basan en postulados naturales. Veamos la prueba.
Sea log a b = t, resulta a t =b. Si elevamos ambas partes a la potencia m: a tn = b n ;
pero como a tn = (a q) nt/q = b n, entonces log a q b n = (n*t)/t, entonces log a q b n = n/q log a b. El teorema ha sido demostrado.
Ejemplos de problemas y desigualdades
Los tipos más comunes de problemas sobre logaritmos son ejemplos de ecuaciones y desigualdades. Se encuentran en casi todos los libros de problemas y también son una parte obligatoria de los exámenes de matemáticas. Para admisión a la universidad o aprobación. exámenes de ingreso En matemáticas es necesario saber cómo resolver este tipo de problemas correctamente.

Desafortunadamente, no existe un plan o esquema único para resolver y determinar el valor desconocido del logaritmo, pero se pueden aplicar ciertas reglas a cada desigualdad matemática o ecuación logarítmica. En primer lugar, debe averiguar si la expresión se puede simplificar o conducir a apariencia general. Simplifica los largos expresiones logarítmicas posible si utilizas sus propiedades correctamente. Conozcámoslos rápidamente.
A la hora de resolver ecuaciones logarítmicas debemos determinar qué tipo de logaritmo tenemos: una expresión de ejemplo puede contener un logaritmo natural o uno decimal.
A continuación se muestran ejemplos ln100, ln1026. Su solución se reduce al hecho de que necesitan determinar la potencia a la que la base 10 será igual a 100 y 1026, respectivamente. Para resolver logaritmos naturales, es necesario aplicar identidades logarítmicas o sus propiedades. Veamos ejemplos de resolución de problemas logarítmicos de varios tipos.

Cómo utilizar fórmulas logarítmicas: con ejemplos y soluciones
Entonces, veamos ejemplos del uso de los teoremas básicos sobre logaritmos.
- La propiedad del logaritmo de un producto se puede utilizar en tareas donde es necesario expandir gran valor números b en factores más simples. Por ejemplo, log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. La respuesta es 9.
- log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 - como puede ver, usando la cuarta propiedad de la potencia del logaritmo, logramos resolver una expresión aparentemente compleja e irresoluble. Sólo necesitas factorizar la base y luego quitar los valores del exponente del signo del logaritmo.

Asignaciones del Examen Estatal Unificado
Los logaritmos se encuentran frecuentemente en exámenes de ingreso, especialmente muchos problemas logarítmicos en el Examen Estatal Unificado ( examen estatal para todos los que abandonan la escuela). Por lo general, estas tareas están presentes no solo en la parte A (la parte de prueba más sencilla del examen), sino también en la parte C (las tareas más complejas y voluminosas). El examen requiere precisión y conocimiento perfecto temas "Logaritmos naturales".
Los ejemplos y soluciones a los problemas están tomados de fuentes oficiales. Opciones del examen estatal unificado. Veamos cómo se resuelven tales tareas.
Dado log 2 (2x-1) = 4. Solución:
reescribamos la expresión, simplificándola un poco log 2 (2x-1) = 2 2, por definición del logaritmo obtenemos que 2x-1 = 2 4, por lo tanto 2x = 17; x = 8,5.
- Es mejor reducir todos los logaritmos a la misma base para que la solución no sea engorrosa ni confusa.
- Todas las expresiones bajo el signo del logaritmo se indican como positivas, por lo tanto, cuando se saca como multiplicador el exponente de una expresión que está bajo el signo del logaritmo y como base, la expresión que queda bajo el logaritmo debe ser positiva.
A medida que la sociedad se desarrolló y la producción se volvió más compleja, las matemáticas también se desarrollaron. Paso de lo simple a lo complejo. De la contabilidad ordinaria utilizando el método de suma y resta, con sus repetidas repeticiones, llegamos al concepto de multiplicación y división. La reducción de la operación repetida de multiplicación se convirtió en el concepto de exponenciación. Las primeras tablas de la dependencia de los números de la base y el número de exponenciación fueron compiladas en el siglo VIII por el matemático indio Varasena. A partir de ellos se puede contar el tiempo de aparición de los logaritmos.
Bosquejo histórico
El renacimiento de Europa en el siglo XVI también estimuló el desarrollo de la mecánica. t requirió una gran cantidad de cálculo relacionado con la multiplicación y la división números de varios dígitos. Las mesas antiguas fueron de gran utilidad. Hicieron posible reemplazar operaciones complejas por otras más simples: suma y resta. Un gran paso adelante fue el trabajo del matemático Michael Stiefel, publicado en 1544, en el que hizo realidad la idea de muchos matemáticos. Esto hizo posible utilizar tablas no solo para potencias en forma de números primos, sino también para números racionales arbitrarios.
En 1614, el escocés John Napier, desarrollando estas ideas, introdujo por primera vez nuevo término"logaritmo de un número." Se compilaron nuevas tablas complejas para calcular los logaritmos de senos y cosenos, así como tangentes. Esto redujo enormemente el trabajo de los astrónomos.
Comenzaron a aparecer nuevas tablas que los científicos utilizaron con éxito durante tres siglos. Pasó mucho tiempo antes nueva operación en álgebra adquirió su forma completa. Se dio la definición del logaritmo y se estudiaron sus propiedades.
Sólo en el siglo XX, con la llegada de la calculadora y el ordenador, la humanidad abandonó las antiguas tablas que habían funcionado con éxito durante los siglos XIII.
 Hoy llamamos logaritmo de b en base a al número x que es la potencia de a para formar b. Esto se escribe como una fórmula: x = log a(b).
Hoy llamamos logaritmo de b en base a al número x que es la potencia de a para formar b. Esto se escribe como una fórmula: x = log a(b).
Por ejemplo, log 3(9) sería igual a 2. Esto es obvio si sigues la definición. Si elevamos 3 a la potencia de 2, obtenemos 9.
Por tanto, la definición formulada establece sólo una restricción: los números a y b deben ser reales.
Tipos de logaritmos
La definición clásica se llama logaritmo real y en realidad es la solución de la ecuación a x = b. La opción a = 1 está en el límite y no es de interés. Atención: 1 elevado a cualquier potencia es igual a 1.
Valor real del logaritmo se define solo cuando la base y el argumento son mayores que 0, y la base no debe ser igual a 1.
Lugar especial en el campo de las matemáticas. jugar logaritmos, que se nombrarán dependiendo del tamaño de su base:

Reglas y restricciones
La propiedad fundamental de los logaritmos es la regla: el logaritmo de un producto es igual a la suma logarítmica. log abp = log a(b) + log a(p).
Como variante de esta afirmación será: log c(b/p) = log c(b) - log c(p), la función cociente es igual a la diferencia de las funciones.
De las dos reglas anteriores es fácil ver que: log a(b p) = p * log a(b).
Otras propiedades incluyen:

Comentario. No cometas un error común: el logaritmo de una suma no es igual a la suma de logaritmos.
 Durante muchos siglos, la operación de encontrar un logaritmo fue una tarea que requería bastante tiempo. Los matemáticos utilizaron fórmula bien conocida Teoría logarítmica de la expansión polinomial:
Durante muchos siglos, la operación de encontrar un logaritmo fue una tarea que requería bastante tiempo. Los matemáticos utilizaron fórmula bien conocida Teoría logarítmica de la expansión polinomial:
ln (1 + x) = x — (x^2)/2 + (x^3)/3 — (x^4)/4 + … + ((-1)^(n + 1))*(( x^n)/n), donde n - número natural mayor que 1, lo que determina la precisión del cálculo.
Los logaritmos con otras bases se calcularon utilizando el teorema de la transición de una base a otra y la propiedad del logaritmo del producto.
Dado que este método requiere mucha mano de obra y al resolver problemas prácticos Difícil de implementar, utilizamos tablas de logaritmos precompiladas, lo que aceleró significativamente todo el trabajo.
En algunos casos, se utilizaron gráficos logarítmicos especialmente diseñados, lo que dio menos precisión, pero aceleró significativamente la búsqueda. valor deseado. La curva de la función y = log a(x), construida sobre varios puntos, permite utilizar una regla normal para encontrar el valor de la función en cualquier otro punto. ingenieros mucho tiempo Para estos fines se utilizó el llamado papel cuadriculado.
En el siglo XVII aparecieron las primeras condiciones de computación analógica auxiliar, que siglo 19 adquirió un aspecto acabado. El dispositivo más exitoso se llamó regla de cálculo. A pesar de la simplicidad del dispositivo, su apariencia aceleró significativamente el proceso de todos los cálculos de ingeniería, y esto es difícil de sobreestimar. Actualmente, pocas personas están familiarizadas con este dispositivo.
La llegada de las calculadoras y los ordenadores hizo inútil el uso de cualquier otro dispositivo.
Ecuaciones y desigualdades
Para resolver diversas ecuaciones y desigualdades utilizando logaritmos, se utilizan las siguientes fórmulas:
- Transición de una base a otra: log a(b) = log c(b) / log c(a);
- Como consecuencia versión anterior: log a(b) = 1 / log b(a).
Para resolver desigualdades es útil saber:
- El valor del logaritmo será positivo sólo si la base y el argumento son mayores o menores que uno; si se viola al menos una condición, el valor del logaritmo será negativo.
- Si la función logaritmo se aplica a los lados derecho e izquierdo de una desigualdad, y la base del logaritmo es mayor que uno, entonces se conserva el signo de la desigualdad; de lo contrario cambia.
Problemas de muestra
Consideremos varias opciones para usar logaritmos y sus propiedades. Ejemplos de resolución de ecuaciones:

Considere la opción de colocar el logaritmo en una potencia:
- Problema 3. Calcula 25^log 5(3). Solución: en las condiciones del problema, la entrada es similar a la siguiente (5^2)^log5(3) o 5^(2 * log 5(3)). Escribámoslo de otra manera: 5^log 5(3*2), o el cuadrado de un número como argumento de función se puede escribir como el cuadrado de la función misma (5^log 5(3))^2. Usando las propiedades de los logaritmos, esta expresión es igual a 3^2. Respuesta: como resultado del cálculo obtenemos 9.
Aplicación práctica
Al ser una herramienta puramente matemática, parece lejos de ser vida real que el logaritmo de repente adquirió gran importancia para describir objetos mundo real. Es difícil encontrar una ciencia donde no se utilice. Esto se aplica plenamente no solo a los naturales, sino también zonas humanitarias conocimiento.
Dependencias logarítmicas
A continuación se muestran algunos ejemplos de dependencias numéricas:

mecanica y fisica
Históricamente, la mecánica y la física siempre se han desarrollado utilizando métodos matemáticos investigación y al mismo tiempo sirvió de incentivo para el desarrollo de las matemáticas, incluidos los logaritmos. La teoría de la mayoría de las leyes de la física está escrita en el lenguaje de las matemáticas. Demos sólo dos ejemplos de descripción de leyes físicas utilizando el logaritmo.
El problema de calcular una cantidad tan compleja como la velocidad de un cohete se puede resolver utilizando la fórmula de Tsiolkovsky, que sentó las bases de la teoría de la exploración espacial:
V = I * ln (M1/M2), donde
- V es la velocidad final del avión.
- I – impulso específico del motor.
- M 1 – masa inicial del cohete.
- M 2 – masa final.
Otro ejemplo importante - esto se utiliza en la fórmula de otro gran científico, Max Planck, que sirve para evaluar el estado de equilibrio en termodinámica.
S = k * ln (Ω), donde
- S – propiedad termodinámica.
- k – constante de Boltzmann.
- Ω es el peso estadístico de diferentes estados.
Química
Menos obvio es el uso de fórmulas en química que contienen la proporción de logaritmos. Pongamos sólo dos ejemplos:
- Ecuación de Nernst, la condición del potencial redox del medio en relación con la actividad de las sustancias y la constante de equilibrio.
- El cálculo de constantes como el índice de autólisis y la acidez de la solución tampoco se puede realizar sin nuestra función.
Psicología y biología
 Y no está del todo claro qué tiene que ver la psicología con esto. Resulta que esta función describe bien la fuerza de la sensación como la relación inversa de la intensidad del estímulo a valor más bajo intensidad.
Y no está del todo claro qué tiene que ver la psicología con esto. Resulta que esta función describe bien la fuerza de la sensación como la relación inversa de la intensidad del estímulo a valor más bajo intensidad.
Después ejemplos anteriores Ya no sorprende que el tema de los logaritmos se utilice ampliamente en biología. Se podrían escribir volúmenes enteros sobre formas biológicas correspondientes a espirales logarítmicas.
Otras áreas
Parece que la existencia del mundo es imposible sin conexión con esta función, y ella rige todas las leyes. Especialmente cuando las leyes de la naturaleza están relacionadas con progresión geométrica. Vale la pena consultar el sitio web de MatProfi, donde encontrará muchos ejemplos de este tipo en las siguientes áreas de actividad:

La lista puede ser interminable. Habiendo dominado los principios básicos de esta función, podrá sumergirse en el mundo de la sabiduría infinita.
Entonces, tenemos potencias de dos. Si tomas el número de la línea inferior, podrás encontrar fácilmente la potencia a la que tendrás que elevar dos para obtener este número. Por ejemplo, para obtener 16, debes elevar dos a la cuarta potencia. Y para obtener 64, debes elevar dos a la sexta potencia. Esto se puede ver en la tabla.
Y ahora, en realidad, la definición del logaritmo:
El logaritmo en base a de x es la potencia a la que se debe elevar a para obtener x.
Designación: log a x = b, donde a es la base, x es el argumento, b es a lo que realmente es igual el logaritmo.
Por ejemplo, 2 3 = 8 ⇒ log 2 8 = 3 (el logaritmo en base 2 de 8 es tres porque 2 3 = 8). Con el mismo éxito log 2 64 = 6, ya que 2 6 = 64.
La operación de encontrar el logaritmo de un número con una base determinada se llama logaritmización. Entonces, agreguemos una nueva línea a nuestra tabla:
| 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 |
| 2 | 4 | 8 | 16 | 32 | 64 |
| iniciar sesión 2 2 = 1 | iniciar sesión 2 4 = 2 | iniciar sesión 2 8 = 3 | iniciar sesión 2 16 = 4 | iniciar sesión 2 32 = 5 | registro 2 64 = 6 |
Desafortunadamente, no todos los logaritmos se calculan tan fácilmente. Por ejemplo, intente encontrar log 2 5. El número 5 no está en la tabla, pero la lógica dicta que el logaritmo estará en algún lugar del segmento. porque 2 2< 5 < 2 3 , а чем больше степень двойки, тем больше получится число.
Estos números se llaman irracionales: los números después del punto decimal se pueden escribir hasta el infinito y nunca se repiten. Si el logaritmo resulta irracional, es mejor dejarlo así: log 2 5, log 3 8, log 5 100.
Es importante entender que un logaritmo es una expresión con dos variables (la base y el argumento). Al principio, mucha gente confunde dónde está la base y dónde está el argumento. Para evitar molestos malentendidos, basta con mirar la imagen:
Ante nosotros no hay más que la definición de logaritmo. Recordar: el logaritmo es una potencia, en el que se debe construir la base para obtener un argumento. Es la base la que está elevada a una potencia; está resaltada en rojo en la imagen. ¡Resulta que la base siempre está abajo! Les digo a mis alumnos esta maravillosa regla desde la primera lección, y no surge ninguna confusión.
Hemos descubierto la definición; solo queda aprender a contar logaritmos, es decir. deshazte del signo "registro". Para empezar, observamos que de la definición se desprenden dos hechos importantes:
- El argumento y la base siempre deben ser mayores que cero. Esto se desprende de la definición de grado mediante un exponente racional, al que se reduce la definición de logaritmo.
- La base debe ser diferente de uno, ya que uno, en cualquier grado, sigue siendo uno. Debido a esto, la pregunta “¿a qué potencia hay que elevar uno para obtener dos” no tiene sentido. ¡No existe tal grado!
Estas restricciones se denominan rango de valores aceptables(ODZ). Resulta que la ODZ del logaritmo se ve así: log a x = b ⇒ x > 0, a > 0, a ≠ 1.
Tenga en cuenta que no existen restricciones sobre el número b (el valor del logaritmo). Por ejemplo, el logaritmo bien puede ser negativo: log 2 0,5 = −1, porque 0,5 = 2-1.
Sin embargo, ahora sólo estamos considerando expresiones numéricas, donde no es necesario conocer el CVD del logaritmo. Los autores de los problemas ya han tenido en cuenta todas las restricciones. Pero cuando se van ecuaciones logarítmicas y desigualdades, los requisitos del DHS serán obligatorios. Después de todo, la base y el argumento pueden contener construcciones muy sólidas que no necesariamente corresponden a las restricciones anteriores.
Ahora consideremos esquema general calcular logaritmos. Consta de tres pasos:
- Representar la base a y el argumento x como una potencia con el mínimo posible razón, mayor que uno. En el camino, es mejor deshacerse de los decimales;
- Resuelve la ecuación para la variable b: x = a b ;
- El número b resultante será la respuesta.
¡Eso es todo! Si el logaritmo resulta irracional, esto ya será visible en el primer paso. El requisito de que la base sea mayor que uno es muy importante: esto reduce la probabilidad de error y simplifica enormemente los cálculos. Lo mismo con decimales: si los convierte inmediatamente en normales, habrá muchos menos errores.
Veamos cómo funciona este esquema usando ejemplos específicos:
Tarea. Calcula el logaritmo: log 5 25
- Imaginemos la base y el argumento como una potencia de cinco: 5 = 5 1 ; 25 = 5 2 ;
- Recibimos la respuesta: 2.
Creemos y resolvamos la ecuación:
iniciar sesión 5 25 = b ⇒ (5 1) b = 5 2 ⇒ 5 b = 5 2 ⇒ b = 2 ;
Tarea. Calcula el logaritmo:
Tarea. Calcula el logaritmo: log 4 64
- Imaginemos la base y el argumento como una potencia de dos: 4 = 2 2 ; 64 = 2 6 ;
- Creemos y resolvamos la ecuación:
iniciar sesión 4 64 = b ⇒ (2 2) b = 2 6 ⇒ 2 2b = 2 6 ⇒ 2b = 6 ⇒ b = 3 ; - Recibimos la respuesta: 3.
Tarea. Calcula el logaritmo: log 16 1
- Imaginemos la base y el argumento como una potencia de dos: 16 = 2 4 ; 1 = 2 0 ;
- Creemos y resolvamos la ecuación:
iniciar sesión 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4b = 2 0 ⇒ 4b = 0 ⇒ b = 0 ; - Recibimos la respuesta: 0.
Tarea. Calcula el logaritmo: log 7 14
- Imaginemos la base y el argumento como una potencia de siete: 7 = 7 1 ; 14 no se puede representar como una potencia de siete, ya que 7 1< 14 < 7 2 ;
- Del párrafo anterior se desprende que el logaritmo no cuenta;
- La respuesta es ningún cambio: log 7 14.
Una pequeña nota sobre el último ejemplo. ¿Cómo puedes estar seguro de que un número no es una potencia exacta de otro número? Es muy simple: simplemente divídalo en factores primos. Si la expansión tiene al menos dos factores diferentes, el número no es una potencia exacta.
Tarea. Descubra si los números son potencias exactas: 8; 48; 81; 35; 14.
8 = 2 · 2 · 2 = 2 3 - grado exacto, porque sólo hay un multiplicador;
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 2 4 - no es una potencia exacta, ya que existen dos factores: 3 y 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 3 4 - grado exacto;
35 = 7 · 5 - nuevamente no es una potencia exacta;
14 = 7 · 2 - nuevamente no es un grado exacto;
Notemos también que nosotros mismos numeros primos son siempre grados exactos de sí mismos.
logaritmo decimal
Algunos logaritmos son tan comunes que tienen un nombre y símbolo especiales.
El logaritmo decimal de x es el logaritmo en base 10, es decir La potencia a la que se debe elevar el número 10 para obtener el número x. Designación: lg x.
Por ejemplo, registro 10 = 1; lg 100 = 2; lg 1000 = 3-etc.
De ahora en adelante, cuando aparezca una frase como "Buscar LG 0.01" en un libro de texto, sepa: no se trata de un error tipográfico. Este es un logaritmo decimal. Sin embargo, si no estás familiarizado con esta notación, siempre puedes reescribirla:
registro x = registro 10 x
Todo lo que es cierto para los logaritmos ordinarios también lo es para los logaritmos decimales.
logaritmo natural
Hay otro logaritmo que tiene su propia designación. En cierto modo, es incluso más importante que el decimal. se trata de sobre el logaritmo natural.
El logaritmo natural de x es el logaritmo en base e, es decir la potencia a la que se debe elevar el número e para obtener el número x. Designación: ln x .
Muchos se preguntarán: ¿cuál es el número e? Este es un número irracional, su valor exacto imposible de encontrar y registrar. Daré sólo las primeras cifras:
mi = 2,718281828459...
No entraremos en detalles sobre qué es este número y por qué es necesario. Solo recuerda que e es la base del logaritmo natural:
ln x = log e x
Así ln e = 1 ; En mi 2 = 2; En mi 16 = 16 - etc. Por otra parte, ln 2 es un número irracional. En general, el logaritmo natural de cualquier número racional irracional. Excepto, por supuesto, uno: ln 1 = 0.
Para los logaritmos naturales, son válidas todas las reglas que son verdaderas para los logaritmos ordinarios.