Comprueba la solución del mayor y el menor del segmento. El mayor y el menor valor de la función. Tarea B15 (2014)

Veamos cómo explorar una función usando un gráfico. Resulta que mirando el gráfico, puedes encontrar todo lo que nos interesa, a saber:

• alcance de la función
• rango de función
• función ceros
• períodos de aumento y disminución
• puntos altos y bajos
• el valor mayor y menor de la función en el intervalo.

Aclaremos la terminología:

Abscisa es la coordenada horizontal del punto.
ordenada- coordenada vertical.
abscisa- el eje horizontal, más a menudo llamado el eje.
eje Y - eje vertical, o eje .

Argumento es una variable independiente de la que dependen los valores de la función. Más a menudo indicado.
En otras palabras, nosotros mismos elegimos , sustituimos en la fórmula de la función y obtenemos .

Dominio funciones: el conjunto de esos (y solo esos) valores del argumento para el que existe la función.
Denotado: o .

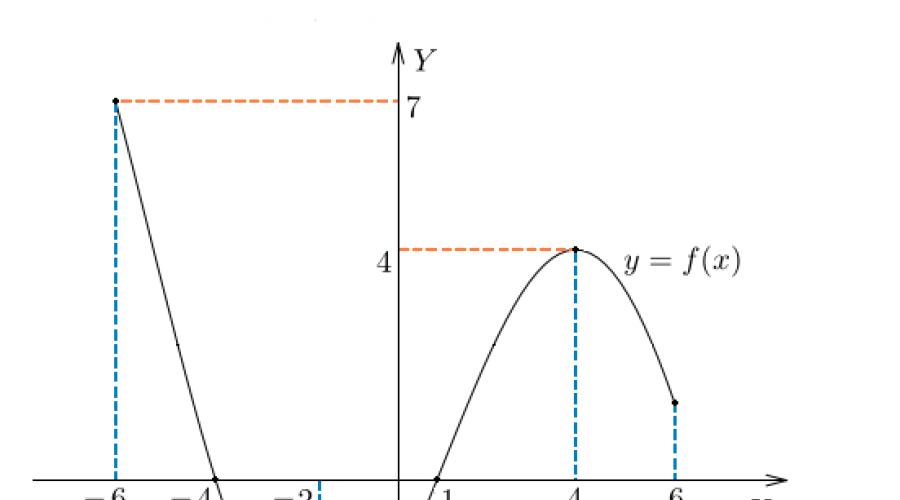
En nuestra figura, el dominio de la función es un segmento. Es en este segmento donde se dibuja la gráfica de la función. Solo aqui función dada existir.

Rango de función es el conjunto de valores que toma la variable. En nuestra figura, este es un segmento, desde el valor más bajo hasta el más alto.

Ceros de función- puntos donde el valor de la función es igual a cero, es decir, . En nuestra figura, estos son los puntos y .

Los valores de la función son positivos donde . En nuestra figura, estos son los intervalos y .
Los valores de la función son negativos. donde . Tenemos este intervalo (o intervalo) de a.

Los conceptos más importantes - funcion creciente y decreciente en algún conjunto. Como conjunto, puedes tomar un segmento, un intervalo, una unión de intervalos o la recta numérica completa.

Función aumenta

En otras palabras, cuanto más, más, es decir, la gráfica va hacia la derecha y hacia arriba.

Función decreciente sobre el conjunto si para alguno y perteneciente al conjunto la desigualdad implica la desigualdad .

Para una función decreciente, un valor mayor corresponde a un valor menor. El gráfico va hacia la derecha y hacia abajo.

En nuestra figura, la función crece en el intervalo y decrece en los intervalos y .

Definamos que es puntos máximos y mínimos de la función.

Punto máximo- este es un punto interno del dominio de definición, tal que el valor de la función en él es mayor que en todos los puntos suficientemente cercanos a él.
En otras palabras, el punto máximo es tal punto, el valor de la función en la que más que en los vecinos. Esta es una "colina" local en el gráfico.

En nuestra figura - el punto máximo.

Punto bajo- un punto interno del dominio de definición, tal que el valor de la función en él es menor que en todos los puntos suficientemente próximos a él.
Es decir, el punto mínimo es tal que el valor de la función en él es menor que en los vecinos. En el gráfico, este es un "agujero" local.

En nuestra figura - el punto mínimo.

El punto es el límite. No es un punto interior del dominio de definición y por lo tanto no se ajusta a la definición de punto máximo. Después de todo, ella no tiene vecinos a la izquierda. De la misma manera, no puede haber un punto mínimo en nuestro gráfico.

Los puntos máximo y mínimo se denominan colectivamente puntos extremos de la función. En nuestro caso, esto es y .

Pero, ¿qué sucede si necesita encontrar, por ejemplo, función mínima en el corte? EN este caso responder: . porque función mínima es su valor en el punto mínimo.

De manera similar, el máximo de nuestra función es . Se alcanza en el punto .

Podemos decir que los extremos de la función son iguales a y .

A veces, en las tareas que necesita para encontrar los valores mayor y menor de la función en un segmento dado. No necesariamente coinciden con los extremos.

En nuestro caso valor de función más pequeño en el intervalo es igual y coincide con el mínimo de la función. Pero su mayor valor en este segmento es igual a . Se alcanza en el extremo izquierdo del segmento.

En cualquier caso, los valores más grandes y más pequeños de una función continua en un segmento se obtienen en los puntos extremos o en los extremos del segmento.

menuda y bonita Tarea simple de la categoría de las que sirven de salvavidas a un estudiante flotante. En la naturaleza, el reino soñoliento de mediados de julio, por lo que es hora de establecerse con una computadora portátil en la playa. A primera hora de la mañana, un rayo de sol de la teoría jugó para pronto centrarse en la práctica, que, a pesar de su declarada levedad, contiene fragmentos de vidrio en la arena. En este sentido, recomiendo considerar concienzudamente algunos ejemplos de esta página. Para resolver tareas prácticas, debe ser capaz de encontrar derivados y entender el material del artículo Intervalos de monotonicidad y extremos de una función.

Primero, brevemente sobre lo principal. En una lección sobre continuidad de funciones Di la definición de continuidad en un punto y continuidad en un intervalo. El comportamiento ejemplar de una función sobre un segmento se formula de manera similar. Una función es continua en un segmento si:

1) es continua en el intervalo ;
2) continua en un punto a la derecha y en el punto izquierda.

El segundo párrafo trata de los llamados continuidad unilateral funciones en un punto. Hay varios enfoques para su definición, pero me mantendré en la línea comenzada anteriormente:

La función es continua en un punto a la derecha, si está definida en un punto dado y su límite por la derecha coincide con el valor de la función en un punto dado: . es continua en el punto izquierda, si se define en un punto dado y su límite izquierdo es igual al valor en ese punto:

Imagina que los puntos verdes son los clavos a los que se une la goma elástica mágica:

Toma mentalmente la línea roja en tus manos. Obviamente, no importa cuánto estiremos la gráfica hacia arriba y hacia abajo (a lo largo del eje), la función seguirá siendo limitado- un seto arriba, un seto abajo, y nuestro producto pasta en un potrero. Por lo tanto, una función continua en un segmento está acotada en él. En el curso del análisis matemático, este hecho aparentemente simple se afirma y se prueba rigurosamente. Primer teorema de Weierstrass.… A muchas personas les molesta que los enunciados elementales se justifiquen tediosamente en matemáticas, pero esto tiene un significado importante. Supongamos que cierto habitante de la Edad Media terry tiró el gráfico hacia el cielo más allá de los límites de visibilidad, esto se insertó. ¡Antes de la invención del telescopio, la función limitada en el espacio no era del todo obvia! De hecho, ¿cómo sabes lo que nos espera más allá del horizonte? Después de todo, una vez que la Tierra se consideró plana, hoy en día incluso la teletransportación ordinaria requiere pruebas =)

De acuerdo a segundo teorema de Weierstrass, continuo en el segmentola función alcanza su borde superior exacto y su borde inferior exacto .

El número también se llama el valor máximo de la función en el segmento y denotado por , y el número - el valor mínimo de la función en el segmento marcado

En nuestro caso:

Nota : en teoría, los registros son comunes .

Mas o menos, valor más alto se encuentra donde está el punto más alto del gráfico, y el más pequeño, donde está el punto más bajo.

¡Importante! Como ya se ha señalado en el artículo sobre extremos de la función, el mayor valor de la función y valor de función más pequeño – NO ES EL MÍSMO, qué función máxima y función mínima. Entonces, en este ejemplo, el número es el mínimo de la función, pero no el valor mínimo.

Por cierto, ¿qué pasa fuera del segmento? Sí, incluso la inundación, en el contexto del problema que estamos considerando, esto no nos interesa en absoluto. La tarea implica solo encontrar dos números. ¡y eso es!

Además, la solución es puramente analítica, por lo tanto, no hay necesidad de dibujar!

El algoritmo se encuentra en la superficie y se sugiere a sí mismo a partir de la figura anterior:

1) Encuentra los valores de la función en puntos críticos, que pertenecen a este segmento.

Atrapa una sorpresa más: no hay necesidad de verificar una condición suficiente para un extremo, ya que, como se acaba de mostrar, la presencia de un mínimo o un máximo aún no garantizado cual es el valor minimo o maximo. La función de demostración alcanza su máximo y, por voluntad del destino, el mismo número es el mayor valor de la función en el intervalo. Pero, por supuesto, tal coincidencia no siempre ocurre.

Así, en el primer paso, es más rápido y sencillo calcular los valores de la función en los puntos críticos pertenecientes al segmento, sin importar si tienen extremos o no.

2) Calculamos los valores de la función en los extremos del segmento.

3) Entre los valores de la función que se encuentran en los párrafos 1 y 2, seleccionamos el más pequeño y el más Número grande, escribe la respuesta.

Nos sentamos en la orilla del mar azul y golpeamos los talones en aguas poco profundas:

Ejemplo 1

Encuentra los valores mayor y menor de una función en un segmento

Decisión:
1) Calcular los valores de la función en los puntos críticos pertenecientes a este segmento:

Calculemos el valor de la función en el segundo punto crítico:

2) Calcular los valores de la función en los extremos del segmento:

3) Se obtuvieron resultados "negritos" con exponenciales y logaritmos, lo que complica significativamente su comparación. Por ello, nos armaremos de una calculadora o Excel y calcularemos los valores aproximados, sin olvidar que:

Ahora todo está claro.

Responder:

Ejemplo fraccionario-racional para decisión independiente:

Ejemplo 6

Encuentre el máximo y valor mínimo funciones en el segmento

El proceso de encontrar los valores más pequeños y más grandes de una función en un segmento recuerda a un fascinante vuelo alrededor de un objeto (el gráfico de una función) en un helicóptero disparando desde un cañón de largo alcance en ciertos puntos y eligiendo entre estos puntos puntos muy especiales para tiros de control. Los puntos se seleccionan de cierta manera y de acuerdo con ciertas reglas. ¿Por qué reglas? Hablaremos de esto más adelante.

Si la función y = F(X) continua en el segmento [ un, b] , luego llega a este segmento menos y valores más altos . Esto puede suceder en puntos extremos o en los extremos del segmento. Por lo tanto, para encontrar menos y los valores más grandes de la función , continua en el segmento [ un, b] , necesitas calcular sus valores en todos puntos críticos y en los extremos del segmento, y luego elige el más pequeño y el más grande de ellos.

Supongamos, por ejemplo, que se requiere determinar el valor máximo de la función F(X) en el segmento [ un, b] . Para hacer esto, encuentre todos sus puntos críticos sobre [ un, b] .

punto crítico se llama el punto en el que función definida, y ella derivado es cero o no existe. Luego debes calcular los valores de la función en los puntos críticos. Y, finalmente, se deben comparar los valores de la función en los puntos críticos y en los extremos del segmento ( F(un) y F(b) ). El mayor de estos números será el mayor valor de la función en el segmento [un, b] .

El problema de encontrar los valores más pequeños de la función .

Estamos buscando los valores más pequeños y más grandes de la función juntos

Ejemplo 1. Encuentra los valores más pequeño y más grande de una función en el segmento [-1, 2] .

Decisión. Encontramos la derivada de esta función. Iguale la derivada a cero () y obtenga dos puntos críticos: y . Para encontrar los valores más pequeños y más grandes de una función en un segmento dado, basta con calcular sus valores en los extremos del segmento y en el punto, ya que el punto no pertenece al segmento [-1, 2] . Estos valores de función son los siguientes: , , . Resulta que valor de función más pequeño(marcado en rojo en el gráfico siguiente), igual a -7, se alcanza en el extremo derecho del segmento - en el punto , y mayor(también rojo en el gráfico), es igual a 9, - en el punto crítico.

Si la función es continua en un cierto intervalo y este intervalo no es un segmento (pero es, por ejemplo, un intervalo; la diferencia entre un intervalo y un segmento: los puntos de la frontera del intervalo no están incluidos en el intervalo, pero el los puntos límite del segmento están incluidos en el segmento), entonces entre los valores de la función puede no haber el más pequeño y el más grande. Entonces, por ejemplo, la función representada en la siguiente figura es continua en ]-∞, +∞[ y no tiene el valor más grande.

Sin embargo, para cualquier intervalo (cerrado, abierto o infinito), se cumple la siguiente propiedad de las funciones continuas.

Ejemplo 4. Encuentra los valores más pequeño y más grande de una función en el segmento [-1, 3] .

Decisión. Encontramos la derivada de esta función como la derivada del cociente:

.

Igualamos la derivada a cero, lo que nos da un punto crítico: . Pertenece al intervalo [-1, 3] . Para encontrar los valores más pequeños y más grandes de una función en un segmento dado, encontramos sus valores en los extremos del segmento y en el punto crítico encontrado:

Comparemos estos valores. Conclusión: igual a -5/13, en el punto y el mayor valor igual a 1 en el punto .

Seguimos buscando juntos los valores más pequeños y más grandes de la función

Hay docentes que en el tema de encontrar los valores menor y mayor de una función, no dan a los alumnos ejemplos más complicados que los recién considerados, es decir, aquellos en los que la función es un polinomio o una fracción, el numerador. y denominador de los cuales son polinomios. Pero no nos limitaremos a tales ejemplos, ya que entre los profesores hay amantes de hacer pensar a los estudiantes en su totalidad (tabla de derivados). Por lo tanto, se utilizará el logaritmo y la función trigonométrica.

Ejemplo 6. Encuentra los valores más pequeño y más grande de una función en el segmento .

Decisión. Encontramos la derivada de esta función como derivado del producto :

Igualamos la derivada a cero, lo que da un punto crítico: . Pertenece al segmento. Para encontrar los valores más pequeños y más grandes de una función en un segmento dado, encontramos sus valores en los extremos del segmento y en el punto crítico encontrado:

El resultado de todas las acciones: la función alcanza su valor mínimo, igual a 0, en un punto y en un punto y el mayor valor igual a mi², en el punto.

Ejemplo 7. Encuentra los valores más pequeño y más grande de una función en el segmento .

Decisión. Encontramos la derivada de esta función:

Igualar la derivada a cero:

El único punto crítico pertenece al segmento. Para encontrar los valores más pequeños y más grandes de una función en un segmento dado, encontramos sus valores en los extremos del segmento y en el punto crítico encontrado:

Conclusión: la función alcanza su valor mínimo, igual a , en el punto y el mayor valor, igual a , en el punto .

En problemas extremos aplicados, encontrar los valores de función más pequeños (más grandes), por regla general, se reduce a encontrar el mínimo (máximo). Pero no son los mínimos o máximos en sí mismos los que tienen mayor interés práctico, sino los valores del argumento en el que se logran. Al resolver problemas aplicados, surge una dificultad adicional: la compilación de funciones que describen el fenómeno o proceso en consideración.

Ejemplo 8 Se debe estañar un tanque de capacidad para 4 personas, que tenga forma de paralelepípedo de base cuadrada y abierto en la parte superior. ¿Cuáles deben ser las dimensiones del tanque para cubrirlo con la menor cantidad de material?

Decisión. Permitir X- lado base h- altura del tanque, S- su superficie sin cubierta, V- su volumen. El área de superficie del tanque se expresa mediante la fórmula, es decir. es una función de dos variables. Para expresar S como una función de una variable, usamos el hecho de que , de donde . Sustituyendo la expresión encontrada h en la fórmula para S:

Examinemos esta función para un extremo. Está definida y diferenciable en todas partes en ]0, +∞[ , y

.

Igualamos la derivada a cero () y encontramos el punto crítico. Además, en , la derivada no existe, pero este valor no está incluido en el dominio de definición y por lo tanto no puede ser un punto extremo. Entonces, - el único punto crítico. Comprobemos la presencia de un extremo usando el segundo signo suficiente. Encontremos la segunda derivada. Cuando la segunda derivada es mayor que cero (). Esto significa que cuando la función alcanza un mínimo . Porque esto mínimo - el único extremo de esta función, es su valor más pequeño. Entonces, el lado de la base del tanque debe ser igual a 2 my su altura.

Ejemplo 9 Del párrafo UN, situado sobre la vía férrea, hasta el punto Con, a una distancia de ella yo, las mercancías deben ser transportadas. El costo de transportar una unidad de peso por unidad de distancia por ferrocarril es igual a , y por carretera es igual a . hasta que punto METRO líneas ferrocarril debe construirse una carretera para que el transporte de mercancías desde PERO en Con era el mas economico AB se supone que el ferrocarril es recto)?

En la práctica, es bastante común usar la derivada para calcular el valor mayor y menor de una función. Realizamos esta acción cuando descubrimos cómo minimizar los costos, aumentar las ganancias, calcular carga óptima para la producción, etc., es decir, en los casos en que sea necesario determinar valor óptimo cualquier parámetro. Para resolver tales problemas correctamente, uno debe tener una buena comprensión de cuál es el valor más grande y más pequeño de una función.

Yandex.RTB R-A-339285-1

Usualmente definimos estos valores dentro de algún intervalo x, que a su vez puede corresponder a todo el alcance de la función o parte de ella. Puede ser un segmento [ a ; b ] , e intervalo abierto (a ; b) , (a ; b ] , [ a ; b) , intervalo infinito (a ; b) , (a ; b ] , [ a ; b) o intervalo infinito - ∞ ; un , (- ∞ ; un ] , [ un ; + ∞) , (- ∞ ; + ∞) .

En este artículo, explicaremos cómo se calculan explícitamente los valores mayor y menor. función dada con una variable y=f(x) y = f (x) .

Definiciones basicas

Comenzamos, como siempre, con la formulación de las principales definiciones.

Definición 1

El mayor valor de la función y = f (x) en algún intervalo x es el valor m a x y = f (x 0) x ∈ X , que, para cualquier valor x x ∈ X , x ≠ x 0, hace que la desigualdad f (x ) ≤ f (x 0) .

Definición 2

El valor más pequeño de la función y = f (x) en algún intervalo x es el valor m i n x ∈ X y = f (x 0) , que, para cualquier valor x ∈ X , x ≠ x 0, hace que la desigualdad f(X f (x) ≥ f (x0) .

Estas definiciones son bastante obvias. Aún más fácil, puedes decir esto: el mayor valor de una función es su mayor gran importancia en un intervalo conocido en la abscisa x 0 , y el menor es el valor más pequeño aceptado en el mismo intervalo en x 0 .

Definición 3

Los puntos estacionarios son tales valores del argumento de la función en los que su derivada se convierte en 0.

¿Por qué necesitamos saber qué son los puntos estacionarios? Para responder a esta pregunta, debemos recordar el teorema de Fermat. De ello se deduce que un punto estacionario es un punto en el que se encuentra el extremo de una función diferenciable (es decir, su mínimo o máximo local). En consecuencia, la función tomará el valor más pequeño o más grande en un cierto intervalo exactamente en uno de los puntos estacionarios.

Otra función puede tomar el valor más grande o más pequeño en aquellos puntos en los que la función misma es definida y su primera derivada no existe.

La primera pregunta que surge al estudiar este tema es: en todos los casos, ¿podemos determinar el valor máximo o mínimo de una función en un intervalo dado? No, no podemos hacer esto cuando los límites del intervalo dado coincidirán con los límites del dominio de definición, o si estamos tratando con un intervalo infinito. También sucede que una función en un intervalo dado o en el infinito tomará infinitesimales o infinitos grandes valores. En estos casos, no es posible determinar el valor mayor y/o menor.

Estos momentos serán más comprensibles después de la imagen en los gráficos:

La primera figura nos muestra una función que toma los valores mayor y menor (m a x y y m i n y) en puntos estacionarios ubicados en el intervalo [ - 6 ; 6].

Examinemos en detalle el caso indicado en el segundo gráfico. Cambiemos el valor del segmento a [ 1 ; 6] y obtenemos que el valor más grande de la función se logrará en el punto con la abscisa en el límite derecho del intervalo, y el más pequeño, en el punto estacionario.

En la tercera figura, las abscisas de los puntos representan los puntos límite del segmento [ - 3 ; 2]. Corresponden al valor mayor y menor de la función dada.

Ahora veamos la cuarta imagen. En él, la función toma m a x y (el valor más grande) y m i n y (el valor más pequeño) en puntos estacionarios en el intervalo abierto (- 6 ; 6) .

Si tomamos el intervalo [ 1 ; 6), entonces podemos decir que el valor más pequeño de la función en él se alcanzará en un punto estacionario. No sabremos el valor máximo. La función podría tomar el mayor valor en x igual a 6 si x = 6 perteneciera al intervalo. Este es el caso que se muestra en la Figura 5.

En el gráfico 6, esta función adquiere el valor más pequeño en el borde derecho del intervalo (- 3 ; 2 ] , y no podemos sacar conclusiones definitivas sobre el valor más grande.

En la figura 7, vemos que la función tendrá m a x y en el punto estacionario, teniendo una abscisa igual a 1 . La función alcanza su valor mínimo en el límite del intervalo del lado derecho. En menos infinito, los valores de la función se aproximarán asintóticamente a y = 3.

Si tomamos un intervalo x ∈ 2 ; + ∞ , entonces veremos que la función dada no tomará ni el valor más pequeño ni el más grande. Si x tiende a 2, entonces los valores de la función tenderán a menos infinito, ya que la recta x = 2 es una asíntota vertical. Si la abscisa tiende a más infinito, entonces los valores de la función se aproximarán asintóticamente a y = 3. Este es el caso que se muestra en la Figura 8.

En este párrafo, daremos una secuencia de acciones que se deben realizar para encontrar el valor más grande o más pequeño de una función en un cierto intervalo.

1. Primero, encontremos el dominio de la función. Verifiquemos si el segmento especificado en la condición está incluido en ella.
2. Ahora calculemos los puntos contenidos en este segmento en los que no existe la primera derivada. La mayoría de las veces se pueden encontrar en funciones cuyo argumento está escrito bajo el signo del módulo, o en funciones de potencia, cuyo exponente es un número fraccionariamente racional.
3. A continuación, averiguamos qué puntos estacionarios caen en un segmento determinado. Para hacer esto, debe calcular la derivada de la función, luego igualarla a 0 y resolver la ecuación resultante, y luego elegir las raíces apropiadas. Si no obtenemos un solo punto estacionario o no caen en un segmento dado, continuamos con el siguiente paso.
4. Determinemos qué valores tomará la función en los puntos estacionarios dados (si corresponde), o en aquellos puntos donde no existe la primera derivada (si corresponde), o calculamos los valores para x = a y x = segundo
5. 5. Tenemos una serie de valores de función, de los cuales ahora debemos elegir el más grande y el más pequeño. Estos serán los valores mayor y menor de la función que necesitamos encontrar.

Veamos cómo aplicar correctamente este algoritmo al resolver problemas.

Ejemplo 1

Condición: se da la función y = x 3 + 4 x 2. Determine su valor mayor y menor en los segmentos [ 1 ; 4] y [-4; - uno ] .

Decisión:

Comencemos por encontrar el dominio de esta función. En este caso, será el conjunto de todos los números reales excepto el 0. En otras palabras, D (y) : x ∈ (- ∞ ; 0) ∪ 0 ; +∞. Ambos segmentos especificados en la condición estarán dentro del área de definición.

Ahora calculamos la derivada de la función según la regla de derivación de una fracción:

y "= x 3 + 4 x 2" = x 3 + 4 " x 2 - x 3 + 4 x 2" x 4 = = 3 x 2 x 2 - (x 3 - 4) 2 x x 4 = x 3 - 8 x3

Aprendimos que la derivada de la función existirá en todos los puntos de los segmentos [ 1 ; 4] y [-4; - uno ] .

Ahora necesitamos determinar los puntos estacionarios de la función. Hagamos esto con la ecuación x 3 - 8 x 3 = 0. Sólo tiene una raíz real, que es 2. Será un punto estacionario de la función y caerá en el primer segmento [ 1 ; 4 ] .

Calculemos los valores de la función en los extremos del primer segmento y en el punto dado, es decir para x = 1, x = 2 y x = 4:

y(1) = 1 3 + 4 1 2 = 5 y(2) = 2 3 + 4 2 2 = 3 y(4) = 4 3 + 4 4 2 = 4 1 4

Hemos obtenido que el mayor valor de la función m a x y x ∈ [ 1 ; 4 ] = y (2) = 3 se logrará en x = 1 , y el menor m i n y x ∈ [ 1 ; 4 ] = y (2) = 3 – en x = 2 .

El segundo segmento no incluye ningún punto estacionario, por lo que necesitamos calcular los valores de la función solo en los extremos del segmento dado:

y (- 1) = (- 1) 3 + 4 (- 1) 2 = 3

Por lo tanto, m a x y x ∈ [ - 4 ; - 1 ] = y (- 1) = 3 , metro yo norte y X ∈ [ - 4 ; - 1 ] = y (- 4) = - 3 3 4 .

Responder: Para el segmento [ 1 ; 4 ] - metro un X y X ∈ [ 1 ; 4 ] = y (2) = 3 , metro yo norte y X ∈ [ 1 ; 4 ] = y (2) = 3 , para el segmento [ - 4 ; - 1 ] - metro un x y x ∈ [ - 4 ; - 1 ] = y (- 1) = 3 , metro yo norte y X ∈ [ - 4 ; - 1 ] = y (- 4) = - 3 3 4 .

Ver imagen:

antes de estudiar Por aquí, le recomendamos que repita cómo calcular correctamente el límite unilateral y el límite en el infinito, así como aprender los métodos básicos para encontrarlos. Para encontrar el valor mayor y/o menor de una función en un intervalo abierto o infinito, realizamos los siguientes pasos en secuencia.

1. Primero debe verificar si el intervalo dado será un subconjunto del dominio de la función dada.
2. Determinemos todos los puntos que están contenidos en el intervalo requerido y en los que no existe la primera derivada. Por lo general, son para funciones donde el argumento está encerrado en el signo del módulo y para funciones de potencia con fraccionario. indicador racional. Si faltan estos puntos, puede continuar con el siguiente paso.
3. Ahora determinamos qué puntos estacionarios caen en un intervalo dado. Primero, igualamos la derivada a 0, resolvemos la ecuación y encontramos las raíces adecuadas. Si no tenemos un solo punto estacionario o no caen en un intervalo dado, inmediatamente vamos a nuevas medidas. Están determinados por el tipo de intervalo.

• Si el intervalo se ve como [ a ; b), entonces necesitamos calcular el valor de la función en el punto x = a y el límite unilateral lím x → b - 0 f (x) .
• Si el intervalo tiene la forma (a ; b ] , entonces necesitamos calcular el valor de la función en el punto x = b y el límite lateral lím x → a + 0 f (x) .
• Si el intervalo tiene la forma (a ; b) , entonces necesitamos calcular los límites unilaterales lím x → b - 0 f (x) , lím x → a + 0 f (x) .
• Si el intervalo se ve como [ a ; + ∞), entonces es necesario calcular el valor en el punto x = a y el límite a más infinito lim x → + ∞ f (x) .
• Si el intervalo se parece a (- ∞ ; b ] , calculamos el valor en el punto x = b y el límite en menos infinito lim x → - ∞ f (x) .
• Si - ∞ ; b , entonces consideramos el límite unilateral lim x → b - 0 f (x) y el límite en menos infinito lim x → - ∞ f (x)
• Si - ∞ ; + ∞ , entonces consideramos los límites a menos y más infinito lim x → + ∞ f (x) , lim x → - ∞ f (x) .

1. Al final, debe sacar una conclusión basada en los valores obtenidos de la función y los límites. Hay muchas opciones aquí. Entonces, si el límite lateral es igual a menos infinito o más infinito, entonces queda claro de inmediato que no se puede decir nada sobre el valor más pequeño y más grande de la función. A continuación consideraremos un ejemplo típico. Descripciones detalladas ayudarle a entender qué es qué. Si es necesario, puede volver a las figuras 4 - 8 en la primera parte del material.

Condición: dada una función y = 3 e 1 x 2 + x - 6 - 4 . Calcular su valor mayor y menor en los intervalos - ∞ ; -4, -∞; - 3 , (- 3 ; 1 ] , (- 3 ; 2) , [ 1 ; 2) , 2 ; + ∞ , [ 4 ; +∞) .

Decisión

En primer lugar, encontramos el dominio de la función. El denominador de la fracción es trinomio cuadrado, que no debe convertirse en 0:

x 2 + x - 6 = 0 re = 1 2 - 4 1 (- 6) = 25 x 1 = - 1 - 5 2 = - 3 x 2 = - 1 + 5 2 = 2 ⇒ re (y) : x ∈ (- ∞ ; - 3) ∪ (- 3 ; 2) ∪ (2 ; + ∞)

Hemos obtenido el alcance de la función, al que pertenecen todos los intervalos especificados en la condición.

Ahora diferenciamos la función y obtenemos:

y "= 3 e 1 x 2 + x - 6 - 4" = 3 e 1 x 2 + x - 6 " = 3 e 1 x 2 + x - 6 1 x 2 + x - 6 " == 3 e 1 x 2 + x - 6 1 "x 2 + x - 6 - 1 x 2 + x - 6" (x 2 + x - 6) 2 = - 3 (2 x + 1) e 1 x 2 + x - 6 x 2 + x - 6 2

En consecuencia, las derivadas de una función existen en todo el dominio de su definición.

Pasemos a encontrar puntos estacionarios. La derivada de la función se convierte en 0 en x = - 1 2 . Este es un punto estacionario que está en los intervalos (- 3 ; 1 ] y (- 3 ; 2) .

Calculemos el valor de la función en x = - 4 para el intervalo (- ∞ ; - 4 ] , así como el límite en menos infinito:

y (- 4) \u003d 3 mi 1 (- 4) 2 + (- 4) - 6 - 4 \u003d 3 mi 1 6 - 4 ≈ - 0. 456 lím x → - ∞ 3 mi 1 x 2 + x - 6 = 3 mi 0 - 4 = - 1

Como 3 e 1 6 - 4 > - 1 , entonces m a x y x ∈ (- ∞ ; - 4 ] = y (- 4) = 3 e 1 6 - 4 . Esto no nos permite determinar de forma única el valor más pequeño de la función. Solo podemos concluir que hay un límite por debajo de -1, ya que es a este valor al que la función se acerca asintóticamente en menos infinito.

Una característica del segundo intervalo es que no tiene un solo punto estacionario ni un solo límite estricto. Por lo tanto, no podemos calcular ni el valor más grande ni el más pequeño de la función. Al definir el límite en menos infinito y como el argumento tiende a - 3 en el lado izquierdo, obtenemos solo el rango de valores:

lím x → - 3 - 0 3 e 1 x 2 + x - 6 - 4 = lím x → - 3 - 0 3 e 1 (x + 3) (x - 3) - 4 = 3 e 1 (- 3 - 0 + 3) (- 3 - 0 - 2) - 4 = = 3 e 1 (+ 0) - 4 = 3 e + ∞ - 4 = + ∞ lím x → - ∞ 3 e 1 x 2 + x - 6 - 4 = 3 y 0 - 4 = - 1

Esto quiere decir que los valores de la función estarán ubicados en el intervalo -1; +∞

Para encontrar el valor máximo de la función en el tercer intervalo, determinamos su valor en el punto estacionario x = - 1 2 si x = 1 . También necesitamos saber el límite unilateral para el caso en que el argumento tiende a - 3 en el lado derecho:

y - 1 2 = 3 mi 1 - 1 2 2 + - 1 2 - 6 - 4 = 3 mi 4 25 - 4 ≈ - 1 . 444 y (1) = 3 mi 1 1 2 + 1 - 6 - 4 ≈ - 1 . 644 lím x → - 3 + 0 3 e 1 x 2 + x - 6 - 4 = lím x → - 3 + 0 3 e 1 (x + 3) (x - 2) - 4 = 3 e 1 - 3 + 0 + 3 (- 3 + 0 - 2) - 4 = = 3 mi 1 (- 0) - 4 = 3 mi - ∞ - 4 = 3 0 - 4 = - 4

Resultó que la función tomará el valor más grande en un punto estacionario m a x y x ∈ (3 ; 1 ] = y - 1 2 = 3 e - 4 25 - 4. En cuanto al valor más pequeño, no podemos determinarlo. Todo lo que saber, es la presencia de un límite inferior a -4.

Para el intervalo (- 3 ; 2), tomemos los resultados del cálculo anterior y una vez más calculemos a qué es igual el límite lateral cuando tiende a 2 desde el lado izquierdo:

y - 1 2 = 3 mi 1 - 1 2 2 + - 1 2 - 6 - 4 = 3 mi - 4 25 - 4 ≈ - 1 . 444 lím x → - 3 + 0 3 e 1 x 2 + x - 6 - 4 = - 4 lím x → 2 - 0 3 e 1 x 2 + x - 6 - 4 = lím x → - 3 + 0 3 e 1 (x + 3) (x - 2) - 4 = 3 e 1 (2 - 0 + 3) (2 - 0 - 2) - 4 = = 3 e 1 - 0 - 4 = 3 e - ∞ - 4 = 3 0 - 4 = - 4

Por lo tanto, m a x y x ∈ (- 3 ; 2) = y - 1 2 = 3 e - 4 25 - 4 , y el valor más pequeño no se puede determinar, y los valores de la función están acotados desde abajo por el número - 4 .

Con base en lo que hicimos en los dos cálculos anteriores, podemos afirmar que en el intervalo [ 1 ; 2) la función tomará el valor más grande en x = 1, y es imposible encontrar el más pequeño.

En el intervalo (2 ; + ∞), la función no alcanzará ni el valor más grande ni el más pequeño, es decir tomará valores del intervalo -1; +∞.

lím x → 2 + 0 3 e 1 x 2 + x - 6 - 4 = lím x → - 3 + 0 3 e 1 (x + 3) (x - 2) - 4 = 3 e 1 (2 + 0 + 3 ) (2 + 0 - 2) - 4 = = 3 mi 1 (+ 0) - 4 = 3 mi + ∞ - 4 = + ∞ lím x → + ∞ 3 mi 1 x 2 + x - 6 - 4 = 3 mi 0 - 4 = - 1

Habiendo calculado cuál será el valor de la función en x = 4 , encontramos que m a x y x ∈ [ 4 ; + ∞) = y (4) = 3 e 1 14 - 4 , y la función dada en más infinito se aproximará asintóticamente a la línea y = - 1 .

Comparemos lo que obtuvimos en cada cálculo con la gráfica de la función dada. En la figura, las asíntotas se muestran con líneas de puntos.

Eso es todo lo que queríamos hablar sobre encontrar el valor más grande y más pequeño de una función. Esas secuencias de acciones que te hemos dado te ayudarán a realizar los cálculos necesarios de la forma más rápida y sencilla posible. Pero recuerde que a menudo es útil averiguar primero en qué intervalos la función disminuirá y en qué intervalos aumentará, después de lo cual se pueden sacar más conclusiones. Para que pueda determinar con mayor precisión el valor mayor y menor de la función y justificar los resultados.

Si nota un error en el texto, resáltelo y presione Ctrl+Enter