1 x par o impar. Funciones pares e impares. Funciones periódicas

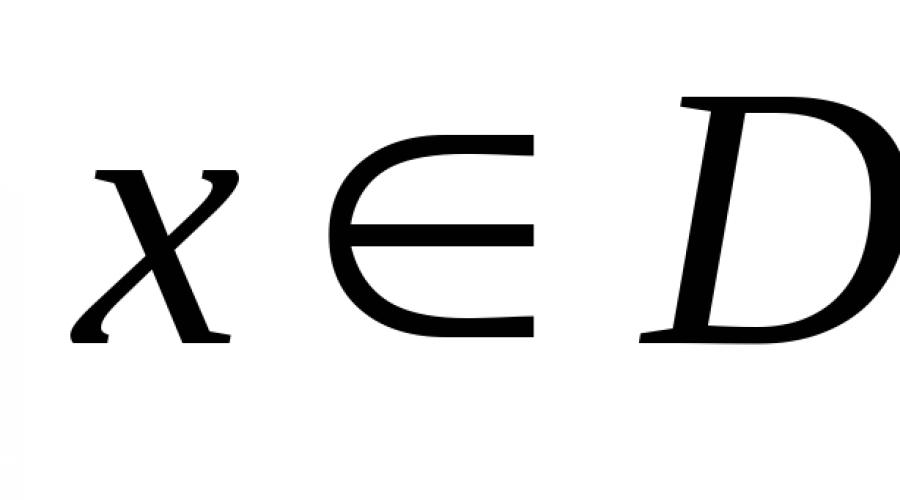
Gráficas de pares y no incluso función tener las siguientes características:

Si una función es par, entonces su gráfica es simétrica con respecto a la ordenada. Si una función es impar, entonces su gráfica es simétrica con respecto al origen.

Solución. Considere la función: \(f\left(x \right)=\left|x \right|\) y sustituya el opuesto \(-x \) en lugar de \(x \). Como resultado de transformaciones simples obtenemos: $$f\left(-x \right)=\left|-x \right|=\left|x \right|=f\left(x \right)$$ En otros Es decir, si reemplaza el argumento con el signo opuesto, la función no cambiará.

Esto significa que esta función es par y su gráfica será simétrica con respecto al eje de ordenadas ( eje vertical). La gráfica de esta función se muestra en la figura de la izquierda. Esto significa que al construir un gráfico, solo puedes dibujar la mitad y la segunda parte (a la izquierda del eje vertical, dibuja simétricamente a la parte derecha). Al determinar la simetría de una función antes de comenzar a trazar su gráfica, puedes simplificar enormemente el proceso de construir o estudiar la función. Si le resulta difícil realizar una comprobación general, puede hacerlo de forma más sencilla: sustituya los mismos valores de diferentes signos en la ecuación. Por ejemplo -5 y 5. Si los valores de la función resultan ser iguales, entonces podemos esperar que la función sea par. Desde un punto de vista matemático, este enfoque no es del todo correcto, pero desde un punto de vista práctico es conveniente. Para aumentar la confiabilidad del resultado, puede sustituir varios pares de valores opuestos.

Solución. Comprobemos lo mismo que en el ejemplo anterior: $$f\left(-x \right)=x\left|-x \right|=-x\left|x \right|=-f\left(x \right ) $$ Esto significa que la función original es impar (el signo de la función ha cambiado al opuesto).

Conclusión: la función es simétrica con respecto al origen. Puedes construir solo la mitad y dibujar la segunda simétricamente. Este tipo de simetría es más difícil de trazar. Esto significa que estás mirando el gráfico desde el otro lado de la hoja, e incluso al revés. O puedes hacer esto: toma la parte dibujada y gírala alrededor del origen 180 grados en sentido antihorario.

Solución. Realicemos la misma verificación de cambio de signo que en los dos ejemplos anteriores. $$f\left(-x \right)=\left(-x \right)^3+\left(-x \right)^2=-x^2+x^2$$ Como resultado, obtenemos que: $$f\left(-x \right)\not=f\left(x \right),f\left(-x \right)\not=-f\left(x \right)$$ Y esto significa que la función no es par ni impar.

Conclusión: la función no es simétrica ni con respecto al origen ni al centro del sistema de coordenadas. Esto sucedió porque es la suma de dos funciones: par e impar. La misma situación ocurrirá si restas dos funciones diferentes. Pero la multiplicación o la división conducirán a un resultado diferente. Por ejemplo, el producto de una función par y una impar produce una función impar. O el cociente de dos números impares da como resultado una función par.

La uniformidad y la imparidad de una función son una de sus principales propiedades, y la paridad ocupa una parte impresionante. curso escolar matemáticas. Determina en gran medida el comportamiento de la función y facilita enormemente la construcción del gráfico correspondiente.

Determinemos la paridad de la función. En términos generales, la función en estudio se considera incluso si para valores opuestos de la variable independiente (x) ubicada en su dominio de definición, los valores correspondientes de y (función) resultan ser iguales.

Demos una definición más estricta. Considere alguna función f (x), que está definida en el dominio D. Será par si para cualquier punto x ubicado en el dominio de definición:

• -x (punto opuesto) también se encuentra en este ámbito,

• f(-x) = f(x).

De la definición anterior se sigue la condición necesaria para el dominio de definición de dicha función, es decir, la simetría con respecto al punto O, que es el origen de las coordenadas, ya que si algún punto b está contenido en el dominio de definición de un par función, entonces el punto correspondiente b también se encuentra en este dominio. Por lo tanto, de lo anterior se desprende la conclusión: la función par tiene una forma simétrica con respecto al eje de ordenadas (Oy).

¿Cómo determinar la paridad de una función en la práctica?

Especifíquelo usando la fórmula h(x)=11^x+11^(-x). Siguiendo el algoritmo que se deriva directamente de la definición, primero examinamos su dominio de definición. Obviamente, está definido para todos los valores del argumento, es decir, se cumple la primera condición.

El siguiente paso es sustituir el valor opuesto (-x) por el argumento (x).
Obtenemos:
h(-x) = 11^(-x) + 11^x.
Dado que la suma satisface la ley conmutativa (conmutativa), es obvio que h(-x) = h(x) y el dado dependencia funcional- incluso.

Comprobemos la paridad de la función h(x)=11^x-11^(-x). Siguiendo el mismo algoritmo, obtenemos que h(-x) = 11^(-x) -11^x. Sacando el menos, al final tenemos
h(-x)=-(11^x-11^(-x))=- h(x). Por tanto, h(x) es impar.

Por cierto, cabe recordar que hay funciones que no se pueden clasificar según estos criterios y se denominan ni pares ni impares;

Incluso las funciones tienen varias propiedades interesantes:

• como resultado de agregar funciones similares, obtienen una igual;
• como resultado de restar tales funciones, se obtiene una par;
• incluso, también incluso;
• como resultado de multiplicar dos de estas funciones, se obtiene una par;
• como resultado de multiplicar funciones pares e impares, se obtiene una impar;
• como resultado de dividir funciones pares e impares, se obtiene una impar;
• la derivada de tal función es impar;
• Si elevas al cuadrado una función impar, obtienes una función par.

La paridad de una función se puede utilizar para resolver ecuaciones.

Para resolver una ecuación como g(x) = 0, donde lado izquierdo La ecuación es una función par, será suficiente encontrar sus soluciones para valores no negativos de la variable. Las raíces resultantes de la ecuación deben combinarse con los números opuestos. Uno de ellos está sujeto a verificación.

Esto también se utiliza con éxito para resolver tareas no estándar con parámetro.

Por ejemplo, ¿hay algún valor del parámetro a para el cual la ecuación 2x^6-x^4-ax^2=1 tendrá tres raíces?

Si tenemos en cuenta que la variable entra en la ecuación en potencias pares, entonces está claro que reemplazar x por - x ecuación dada no cambiará. De ello se deduce que si un determinado número es su raíz, entonces el número opuesto también es la raíz. La conclusión es obvia: las raíces de una ecuación distintas de cero se incluyen en el conjunto de sus soluciones “por pares”.

Está claro que el número en sí no es 0, es decir, el número de raíces de dicha ecuación solo puede ser par y, naturalmente, para cualquier valor del parámetro no puede tener tres raíces.

Pero el número de raíces de la ecuación 2^x+ 2^(-x)=ax^4+2x^2+2 puede ser impar y para cualquier valor del parámetro. De hecho, es fácil comprobar que el conjunto de raíces de esta ecuación contiene soluciones “por pares”. Comprobemos si 0 es una raíz. Cuando lo sustituimos en la ecuación, obtenemos 2=2. Así, además de los "pareados", 0 también es raíz, lo que demuestra su número impar.

Definición 1. La función se llama. incluso (extraño ), si junto con cada valor de variable
significado - X también pertenece
y la igualdad se mantiene

Por lo tanto, una función puede ser par o impar sólo si su dominio de definición es simétrico con respecto al origen de coordenadas en la recta numérica (número X Y - X pertenecen al mismo tiempo
). Por ejemplo, la función
no es par ni impar, ya que su dominio de definición
no simétrico respecto al origen.

Función
incluso, porque
simétrico con respecto al origen y.

Función
extraño, porque
Y
.

Función
no es par e impar, ya que aunque
y es simétrico respecto al origen, no se satisfacen las igualdades (11.1). Por ejemplo,.

La gráfica de una función par es simétrica con respecto al eje. UNED, porque si el punto

También pertenece al horario. La gráfica de una función impar es simétrica con respecto al origen, ya que si
pertenece a la gráfica, entonces el punto
También pertenece al horario.

Para demostrar si una función es par o impar, las siguientes afirmaciones son útiles.

Teorema 1. a) La suma de dos funciones pares (impar) es una función par (impar).

b) El producto de dos funciones pares (impar) es una función par.

c) El producto de una función par e impar es una función impar.

d) Si F– función uniforme en el televisor X, y la función gramo definido en el set
, entonces la función
- incluso.

d) Si F– función impar en el set X, y la función gramo definido en el set
e incluso (impar), entonces la función
– par (impar).

Prueba. Demostremos, por ejemplo, b) yd).

b) dejar
Y
– incluso funciones. Entonces, por tanto. El caso de funciones impares se trata de manera similar.
Y
.

d) dejar F es una función par. Entonces.

Los restantes enunciados del teorema se pueden demostrar de manera similar. El teorema ha sido demostrado.

Teorema 2. Cualquier función
, definido en el set X, simétrica con respecto al origen, se puede representar como una suma de funciones pares e impares.

Prueba. Función
se puede escribir en la forma

.

Función
– incluso, porque
, y la función
– extraño, porque. De este modo,
, Dónde
– incluso, y
– funciones impares. El teorema ha sido demostrado.

Definición 2. Función
llamado periódico , si hay un número
, de modo que para cualquier
números
Y
también pertenecen al dominio de la definición
y las igualdades se satisfacen

tal numero t llamado período funciones
.

De la Definición 1 se deduce que si t– período de la función
, entonces el número – t Mismo es el periodo de la función
(ya que al reemplazar t en - t se mantiene la igualdad). Utilizando el método de inducción matemática se puede demostrar que si t– período de la función F, entonces
, también es un período. De ello se deduce que si una función tiene un período, entonces tiene infinitos períodos.

Definición 3. El más pequeño de los períodos positivos de una función se llama período principal período.

Teorema 3. Si t– período principal de la función F, entonces los períodos restantes son múltiplos de él.

Prueba. Supongamos lo contrario, es decir, que hay un período funciones F (>0), no múltiples t. Luego, dividiendo en t con el resto obtenemos
, Dónde
. Es por eso

eso es – período de la función F, y
, y esto contradice el hecho de que t– período principal de la función F. El enunciado del teorema se deriva de la contradicción resultante. El teorema ha sido demostrado.

Es bien sabido que las funciones trigonométricas son periódicas. Periodo principal
Y
es igual
,
Y
. Encontremos el período de la función.
. Dejar
- el período de esta función. Entonces

(porque
.

o o
.

Significado t, determinada a partir de la primera igualdad, no puede ser un período, ya que depende de X, es decir. es una función de X, y no un número constante. El período se determina a partir de la segunda igualdad:
. Hay infinitos periodos, con
el período positivo más pequeño se obtiene en
:
. Este es el período principal de la función.
.

Un ejemplo de una función periódica más compleja es la función de Dirichlet.

Tenga en cuenta que si t es un número racional, entonces
Y
son números racionales para racionales X e irracional cuando irracional X. Es por eso

para cualquier número racional t. Por lo tanto, cualquier número racional t es el período de la función de Dirichlet. Es claro que esta función no tiene un período principal, ya que existen resultados positivos. numeros racionales, arbitrariamente cercano a cero (por ejemplo, se puede elegir un número racional norte arbitrariamente cercano a cero).

Teorema 4. Si la función F definido en el set X y tiene un periodo t, y la función gramo definido en el set
, entonces una función compleja
también tiene un período t.

Prueba. Tenemos, por lo tanto

es decir, el enunciado del teorema está demostrado.

Por ejemplo, desde porque X tiene un periodo
, entonces las funciones
tener un periodo
.

Definición 4. Las funciones que no son periódicas se llaman no PERIODICO .

Función es uno de los conceptos matemáticos más importantes. Función - dependencia variable en de variable X, si cada valor X coincide con un solo valor en. Variable X llamada variable independiente o argumento. Variable en llamada variable dependiente. Todos los valores de la variable independiente (variable X) forman el dominio de definición de la función. Todos los valores que toma la variable dependiente (variable y), forman el rango de valores de la función.

Gráfico de funciones llame al conjunto de todos los puntos del plano coordenado, cuyas abscisas son iguales a los valores del argumento, y las ordenadas son iguales a los valores correspondientes de la función, es decir, los valores de la Las variables se trazan a lo largo del eje de abscisas. X, y los valores de la variable se trazan a lo largo del eje de ordenadas y. Para graficar una función, necesitas conocer las propiedades de la función. ¡Las principales propiedades de la función se discutirán a continuación!

Para construir una gráfica de una función, recomendamos utilizar nuestro programa: Graficar funciones en línea. Si tiene alguna pregunta mientras estudia el material de esta página, siempre puede hacerla en nuestro foro. ¡También en el foro te ayudarán a resolver problemas de matemáticas, química, geometría, teoría de probabilidades y muchas otras materias!

Propiedades básicas de las funciones.

1) Dominio de función y rango de función.

El dominio de una función es el conjunto de todos los valores válidos de los argumentos válidos. X(variable X), para lo cual la función y = f(x) determinado.
El rango de una función es el conjunto de todos los valores reales. y, que la función acepta.

EN matemáticas elementales Las funciones se estudian sólo en el conjunto de los números reales.

2) Función ceros.

Valores X, en el cual y=0, llamado función ceros. Estas son las abscisas de los puntos de intersección del gráfico de funciones con el eje Ox.

3) Intervalos de signo constante de una función.

Los intervalos de signo constante de una función son tales intervalos de valores. X, en el que los valores de la función y solo se llaman positivos o solo negativos intervalos de signo constante de la función.

4) Monotonicidad de la función..

Una función creciente (en un intervalo determinado) es una función para la cual valor mas alto el argumento de este intervalo corresponde a un valor mayor de la función.

Una función decreciente (en un intervalo determinado) es una función en la que un valor mayor del argumento de este intervalo corresponde a un valor menor de la función.

5) Función par (impar).

Una función par es una función cuyo dominio de definición es simétrico con respecto al origen y para cualquier X f(-x) = f(x). La gráfica de una función par es simétrica con respecto a la ordenada.

Una función impar es una función cuyo dominio de definición es simétrico con respecto al origen y para cualquier X desde el dominio de la definición la igualdad es verdadera f(-x) = -f(x)). La gráfica de una función impar es simétrica con respecto al origen.

incluso función
1) El dominio de definición es simétrico con respecto al punto (0; 0), es decir, si el punto a pertenece al dominio de la definición, entonces el punto -a también pertenece al dominio de la definición.
2) Por cualquier valor X f(-x)=f(x)
3) La gráfica de una función par es simétrica con respecto al eje Oy.

Función impar tiene las siguientes propiedades:
1) El dominio de definición es simétrico con respecto al punto (0; 0).
2) por cualquier valor X, perteneciente al dominio de la definición, la igualdad f(-x)=-f(x)
3) La gráfica de una función impar es simétrica con respecto al origen (0; 0).

No todas las funciones son pares o impares. Funciones vista general no son ni pares ni impares.

6) Funciones limitadas e ilimitadas.

Una función se llama acotada si existe un número positivo M tal que |f(x)| ≤ M para todos los valores de x. Si tal número no existe, entonces la función es ilimitada.

7) Periodicidad de la función.

Una función f(x) es periódica si existe un número T distinto de cero tal que para cualquier x del dominio de definición de la función se cumple lo siguiente: f(x+T) = f(x). Este número más pequeño se llama periodo de la función. Todo funciones trigonométricas son periódicos. (Fórmulas trigonométricas).

Función F se llama periódico si existe un número tal que para cualquier X desde el dominio de la definición la igualdad f(x)=f(x-T)=f(x+T). t es el período de la función.

Toda función periódica tiene conjunto infinito períodos. En la práctica, se suele considerar el período positivo más pequeño.

Los valores de una función periódica se repiten después de un intervalo igual al período. Esto se utiliza al construir gráficos.

La dependencia de una variable y de una variable x, en la que cada valor de x corresponde a un único valor de y, se llama función. Para la designación utilice la notación y=f(x). Cada función tiene una serie de propiedades básicas, como monotonicidad, paridad, periodicidad y otras.

Eche un vistazo más de cerca a la propiedad de paridad.

Se llama a una función y=f(x) incluso si satisface las dos condiciones siguientes:

2. El valor de la función en el punto x, perteneciente al dominio de definición de la función, debe ser igual al valor de la función en el punto -x. Es decir, para cualquier punto x, se debe satisfacer la siguiente igualdad desde el dominio de definición de la función: f(x) = f(-x).

Gráfica de una función par

Si trazas la gráfica de una función par, será simétrica con respecto al eje Oy.

Por ejemplo, la función y=x^2 es par. Vamos a ver. El dominio de definición es todo el eje numérico, lo que significa que es simétrico con respecto al punto O.

Tomemos un x=3 arbitrario. f(x)=3^2=9.

f(-x)=(-3)^2=9. Por lo tanto f(x) = f(-x). Por tanto, se cumplen ambas condiciones, lo que significa que la función es par. A continuación se muestra una gráfica de la función y=x^2.

La figura muestra que la gráfica es simétrica con respecto al eje Oy.

Gráfica de una función impar

Una función y=f(x) se llama impar si satisface las dos condiciones siguientes:

1. El dominio de definición de una función dada debe ser simétrico con respecto al punto O. Es decir, si algún punto a pertenece al dominio de definición de la función, entonces el punto correspondiente -a también debe pertenecer al dominio de definición. de la función dada.

2. Para cualquier punto x, se debe satisfacer la siguiente igualdad desde el dominio de definición de la función: f(x) = -f(x).

La gráfica de una función impar es simétrica con respecto al punto O, el origen de las coordenadas. Por ejemplo, la función y=x^3 es impar. Vamos a ver. El dominio de definición es todo el eje numérico, lo que significa que es simétrico con respecto al punto O.

Tomemos un x=2 arbitrario. f(x)=2^3=8.

f(-x)=(-2)^3=-8. Por lo tanto f(x) = -f(x). Por tanto, se cumplen ambas condiciones, lo que significa que la función es impar. A continuación se muestra una gráfica de la función y=x^3.

La figura muestra claramente que la función impar y=x^3 es simétrica con respecto al origen.