Fermat's Last Theorem: Wiles and Perelman's proof, formulas, calculation rules and complete proof of the theorem. The proof of Fermat's theorem is elementary, simple, understandable. A theorem that cannot be proven.

So, Fermat's Last Theorem (often called Fermat's last theorem), formulated in 1637 by the brilliant French mathematician Pierre Fermat, is very simple in nature and understandable to anyone with a secondary education. It says that the formula a to the power of n + b to the power of n = c to the power of n does not have natural (that is, not fractional) solutions for n > 2. Everything seems simple and clear, but the best mathematicians and ordinary amateurs struggled with searching for a solution for more than three and a half centuries.

Grigory Perelman. refusenik

Vasily Maksimov

In August 2006, the names of the best mathematicians on the planet were announced who received the prestigious Fields Medal - a kind of analogue of the Nobel Prize, which mathematicians, at the whim of Alfred Nobel, were deprived of. The Fields Medal - in addition to a badge of honor, the winners are awarded a check for fifteen thousand Canadian dollars - is awarded by the International Congress of Mathematicians every four years. It was established by Canadian scientist John Charles Fields and was first awarded in 1936. Since 1950, the Fields Medal has been awarded regularly personally by the King of Spain for his contribution to the development of mathematical science. Prize winners can be from one to four scientists under the age of forty. Forty-four mathematicians, including eight Russians, have already received the prize.

Grigory Perelman. Henri Poincaré.

In 2006, the laureates were the Frenchman Wendelin Werner, the Australian Terence Tao and two Russians - Andrey Okunkov working in the USA and Grigory Perelman, a scientist from St. Petersburg. However, at the last moment it became known that Perelman refused this prestigious award - as the organizers announced, “for reasons of principle.”

Such an extravagant act by the Russian mathematician did not come as a surprise to people who knew him. This is not the first time he has refused mathematical awards, explaining his decision by saying that he does not like ceremonial events and unnecessary hype around his name. Ten years ago, in 1996, Perelman refused the European Mathematical Congress prize, citing the fact that he had not completed the work on the scientific problem nominated for the award, and this was not the last case. The Russian mathematician seemed to make it his life’s goal to surprise people, going against public opinion and the scientific community.

Grigory Yakovlevich Perelman was born on June 13, 1966 in Leningrad. From a young age, he was fond of exact sciences, brilliantly graduated from the famous 239th secondary school with in-depth study of mathematics, won numerous mathematical Olympiads: for example, in 1982, as part of a team of Soviet schoolchildren, he participated in the International Mathematical Olympiad, held in Budapest. Perelman was enrolled in Mechanics and Mathematics at Leningrad University without exams, where he studied with excellent marks, continuing to win mathematical competitions at all levels. After graduating from the university with honors, he entered graduate school at the St. Petersburg branch of the Steklov Mathematical Institute. His scientific supervisor was the famous mathematician Academician Aleksandrov. Having defended his Ph.D. thesis, Grigory Perelman remained at the institute, in the laboratory of geometry and topology. His work on the theory of Alexandrov spaces is known; he was able to find evidence for a number of important conjectures. Despite numerous offers from leading Western universities, Perelman prefers to work in Russia.

His most notable success was the solution in 2002 of the famous Poincaré conjecture, published in 1904 and since then remained unproven. Perelman worked on it for eight years. The Poincaré conjecture was considered one of the greatest mathematical mysteries, and its solution was considered the most important achievement in mathematical science: it would immediately advance research into the problems of the physical and mathematical foundations of the universe. The most prominent minds on the planet predicted its solution only in a few decades, and the Clay Institute of Mathematics in Cambridge, Massachusetts, included the Poincaré problem among the seven most interesting unsolved mathematical problems of the millennium, for the solution of each of which a million dollar prize was promised (Millennium Prize Problems). .

The conjecture (sometimes called the problem) of the French mathematician Henri Poincaré (1854–1912) is formulated as follows: any closed simply connected three-dimensional space is homeomorphic to a three-dimensional sphere. To clarify, use a clear example: if you wrap an apple with a rubber band, then, in principle, by tightening the tape, you can compress the apple into a point. If you wrap a donut with the same tape, you cannot compress it to a point without tearing either the donut or the rubber. In this context, an apple is called a “simply connected” figure, but a donut is not simply connected. Almost a hundred years ago, Poincaré established that a two-dimensional sphere is simply connected, and suggested that a three-dimensional sphere is also simply connected. The best mathematicians in the world could not prove this hypothesis.

To qualify for the Clay Institute Prize, Perelman only had to publish his solution in one of the scientific journals, and if within two years no one could find an error in his calculations, then the solution would be considered correct. However, Perelman deviated from the rules from the very beginning, publishing his decision on the preprint website of the Los Alamos Scientific Laboratory. Perhaps he was afraid that an error had crept into his calculations - a similar story had already happened in mathematics. In 1994, the English mathematician Andrew Wiles proposed a solution to Fermat’s famous theorem, and a few months later it turned out that an error had crept into his calculations (however, it was later corrected, and the sensation still took place). There is still no official publication of the proof of the Poincaré conjecture, but there is an authoritative opinion of the best mathematicians on the planet confirming the correctness of Perelman’s calculations.

The Fields Medal was awarded to Grigory Perelman precisely for solving the Poincaré problem. But the Russian scientist refused the prize, which he undoubtedly deserves. “Gregory told me that he feels isolated from the international mathematical community, outside this community, and therefore does not want to receive the award,” Englishman John Ball, president of the World Union of Mathematicians (WUM), said at a press conference in Madrid.

There are rumors that Grigory Perelman is going to leave science altogether: six months ago he resigned from his native Steklov Mathematical Institute, and they say that he will no longer study mathematics. Perhaps the Russian scientist believes that by proving the famous hypothesis, he has done everything he could for science. But who will undertake to discuss the train of thought of such a bright scientist and extraordinary person?.. Perelman refuses any comments, and he told The Daily Telegraph newspaper: “None of what I can say is of the slightest public interest.” However, leading scientific publications were unanimous in their assessments when they reported that “Grigory Perelman, having resolved the Poincaré theorem, stood on a par with the greatest geniuses of the past and present.”

Monthly literary and journalistic magazine and publishing house.

In the 17th century, a lawyer and part-time mathematician Pierre Fermat lived in France, who devoted long hours of leisure to his hobby. One winter evening, sitting by the fireplace, he put forward one very curious statement from the field of number theory - it was this that was later called Fermat’s Great Theorem. Perhaps the excitement would not have been so significant in mathematical circles if one event had not happened. The mathematician often spent his evenings studying his favorite book “Arithmetic” by Diophantus of Alexandria (3rd century), while writing down important thoughts in its margins - this rarity was carefully preserved for posterity by his son. So, on the wide margins of this book, Fermat’s hand left the following inscription: “I have a rather striking proof, but it is too large to be placed in the margins.” It was this recording that caused the stunning excitement around the theorem. Mathematicians had no doubt that the great scientist declared that he had proven his own theorem. You are probably asking the question: “Did he really prove it, or was it a banal lie, or maybe there are other versions of why this note, which did not allow mathematicians of subsequent generations to sleep peacefully, ended up in the margins of the book?”

The essence of the Great Theorem

Fermat’s fairly well-known theorem is simple in its essence and lies in the fact that, provided that n is greater than two, a positive number, the equation X n + Y n = Z n will not have solutions of zero type within the framework of natural numbers. This seemingly simple formula masked incredible complexity, and its proof was fought over for three centuries. There is one strange thing - the theorem was late in its birth, since its special case with n = 2 appeared 2200 years ago - this is the no less famous Pythagorean theorem.

It should be noted that the story concerning Fermat’s well-known theorem is very instructive and entertaining, and not only for mathematicians. What is most interesting is that science was not a job for the scientist, but a simple hobby, which in turn gave the Farmer great pleasure. He also constantly kept in touch with a mathematician, and also a friend, and shared ideas, but oddly enough, he did not strive to publish his own works.

Works of the mathematician Farmer

As for the Farmer’s works themselves, they were discovered precisely in the form of ordinary letters. In some places entire pages were missing, and only fragments of correspondence survived. More interesting is the fact that for three centuries scientists have been looking for the theorem that was discovered in the works of Farmer.

But no matter who dared to prove it, the attempts were reduced to “zero.” The famous mathematician Descartes even accused the scientist of boasting, but it all boiled down to just the most common envy. In addition to creating it, the Farmer also proved his own theorem. True, the solution was found for the case where n=4. As for the case for n=3, it was discovered by the mathematician Euler.

How they tried to prove Farmer's theorem

At the very beginning of the 19th century, this theorem continued to exist. Mathematicians found many proofs of theorems that were limited to natural numbers within two hundred.

And in 1909, a rather large sum was put at stake, equal to one hundred thousand marks of German origin - and all this just to resolve the issue related to this theorem. The prize fund itself was left by a wealthy mathematics lover, Paul Wolfskehl, originally from Germany; by the way, it was he who wanted to “kill himself,” but thanks to such involvement in Fermer’s theorem, he wanted to live. The resulting excitement gave rise to tons of “proofs” that flooded German universities, and among mathematicians the nickname “farmist” was born, which was half-contemptuously used to describe any ambitious upstart who was unable to provide clear evidence.

Conjecture of the Japanese mathematician Yutaka Taniyama

Shifts in the history of the Great Theorem were not observed until the mid-20th century, but one interesting event did occur. In 1955, Japanese mathematician Yutaka Taniyama, who was 28 years old, showed the world a statement from a completely different mathematical field - his hypothesis, unlike Fermat’s, was ahead of its time. It says: “Each elliptic curve corresponds to a certain modular shape.” It seems absurd for every mathematician, like the idea that a tree consists of a certain metal! The paradoxical hypothesis, like most other stunning and ingenious discoveries, was not accepted, since they simply had not yet grown up to it. And Yutaka Taniyama committed suicide three years later - an inexplicable act, but probably honor for a true samurai genius was above all else.

The hypothesis was not remembered for a whole decade, but in the seventies it rose to the peak of popularity - it was confirmed by everyone who could understand it, but, like Fermat’s theorem, it remained unproven.

How are Taniyama's conjecture and Fermat's theorem related?

15 years later, a key event occurred in mathematics, and it united the hypothesis of the famous Japanese and Fermat’s theorem. Gerhard Gray stated that when the Taniyama conjecture is proven, then there will be proofs of Fermat's theorem. That is, the latter is a consequence of Taniyama’s conjecture, and after a year and a half, Fermat’s theorem was proven by University of California professor Kenneth Ribet.

As time passed, regression was replaced by progress, and science rapidly moved forward, especially in the field of computer technology. Thus, the value of n began to increase more and more.

At the very end of the 20th century, the most powerful computers were located in military laboratories; programming was carried out to output a solution to the well-known Fermat problem. As a consequence of all attempts, it was revealed that this theorem is correct for many values ​​of n, x, y. But, unfortunately, this did not become final proof, since there were no specifics as such.

John Wiles proved Fermat's great theorem

And finally, only at the end of 1994, a mathematician from England, John Wiles, found and demonstrated an accurate proof of Fermer’s controversial theorem. Then, after many modifications, discussions on this issue came to their logical conclusion.

The refutation was published on more than a hundred pages of one magazine! Moreover, the theorem was proven using a more modern apparatus of higher mathematics. And what is surprising is that at the time when the Farmer wrote his work, such a device did not exist in nature. In a word, the man was recognized as a genius in this field, which no one could argue with. Despite everything that happened, today you can be sure that the presented theorem of the great scientist Farmer is justified and proven, and not a single mathematician with common sense will start a debate on this topic, which even the most inveterate skeptics of all mankind agree with.

The full name of the person after whom the theorem was presented was named Pierre de Fermer. He made contributions to a wide variety of areas of mathematics. But, unfortunately, most of his works were published only after his death.

There are not many people in the world who have never heard of Fermat’s Last Theorem - perhaps this is the only mathematical problem that has become so widely known and has become a real legend. It is mentioned in many books and films, and the main context of almost all mentions is the impossibility of proving the theorem.

Yes, this theorem is very well known and, in a sense, has become an “idol” worshiped by amateur and professional mathematicians, but few people know that its proof was found, and this happened back in 1995. But first things first.

So, Fermat's Last Theorem (often called Fermat's last theorem), formulated in 1637 by the brilliant French mathematician Pierre Fermat, is very simple in essence and understandable to anyone with a secondary education. It says that the formula a to the power of n + b to the power of n = c to the power of n does not have natural (that is, not fractional) solutions for n > 2. Everything seems simple and clear, but the best mathematicians and ordinary amateurs struggled with searching for a solution for more than three and a half centuries.

Why is she so famous? Now we'll find out...

Are there many proven, unproven and as yet unproven theorems? The point here is that Fermat's Last Theorem represents the greatest contrast between the simplicity of the formulation and the complexity of the proof. Fermat's Last Theorem is an incredibly difficult task, and yet its formulation can be understood by anyone with the 5th grade of high school, but not even every professional mathematician can understand the proof. Neither in physics, nor in chemistry, nor in biology, nor in mathematics, is there a single problem that could be formulated so simply, but remained unsolved for so long. 2. What does it consist of?

Let's start with Pythagorean pants. The wording is really simple - at first glance. As we know from childhood, “Pythagorean pants are equal on all sides.” The problem looks so simple because it was based on a mathematical statement that everyone knows - the Pythagorean theorem: in any right triangle, the square built on the hypotenuse is equal to the sum of the squares built on the legs.

In the 5th century BC. Pythagoras founded the Pythagorean brotherhood. The Pythagoreans, among other things, studied integer triplets satisfying the equality x²+y²=z². They proved that there are infinitely many Pythagorean triples and obtained general formulas for finding them. They probably tried to look for C's and higher degrees. Convinced that this did not work, the Pythagoreans abandoned their useless attempts. The members of the brotherhood were more philosophers and aesthetes than mathematicians.

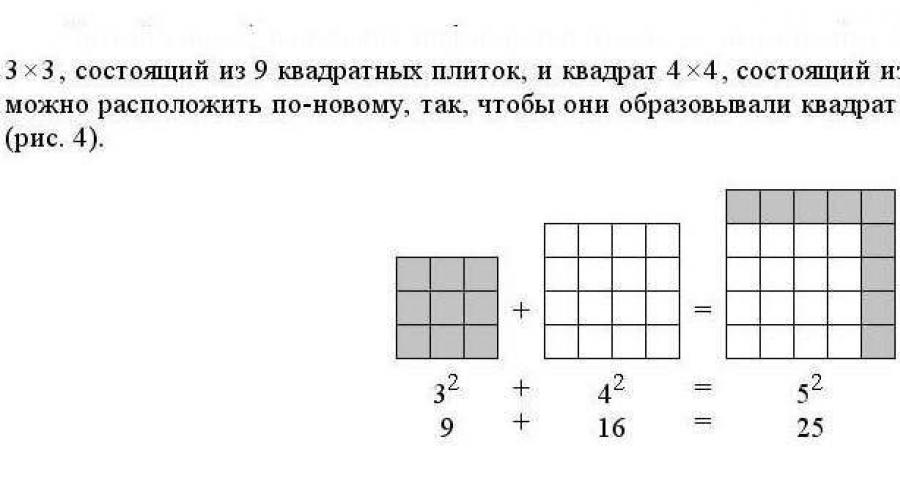
That is, it is easy to select a set of numbers that perfectly satisfy the equality x²+y²=z²

Starting from 3, 4, 5 - indeed, a junior student understands that 9 + 16 = 25.

Or 5, 12, 13: 25 + 144 = 169. Great.

So, it turns out that they are NOT. This is where the trick begins. Simplicity is apparent, because it is difficult to prove not the presence of something, but, on the contrary, its absence. When you need to prove that there is a solution, you can and should simply present this solution.

Proving absence is more difficult: for example, someone says: such and such an equation has no solutions. Put him in a puddle? easy: bam - and here it is, the solution! (give solution). And that’s it, the opponent is defeated. How to prove absence?

Say: “I haven’t found such solutions”? Or maybe you weren't looking well? What if they exist, only very large, very large, such that even a super-powerful computer still doesn’t have enough strength? This is what’s difficult.

This can be shown visually like this: if you take two squares of suitable sizes and disassemble them into unit squares, then from this bunch of unit squares you get a third square (Fig. 2):


But let’s do the same with the third dimension (Fig. 3) - it doesn’t work. There are not enough cubes, or there are extra ones left:

But the 17th century mathematician Frenchman Pierre de Fermat enthusiastically studied the general equation x n + y n = z n. And finally, I concluded: for n>2 there are no integer solutions. Fermat's proof is irretrievably lost. Manuscripts are burning! All that remains is his remark in Diophantus’ Arithmetic: “I have found a truly amazing proof of this proposition, but the margins here are too narrow to contain it.”

Actually, a theorem without proof is called a hypothesis. But Fermat has a reputation for never making mistakes. Even if he did not leave evidence of a statement, it was subsequently confirmed. Moreover, Fermat proved his thesis for n=4. Thus, the hypothesis of the French mathematician went down in history as Fermat’s Last Theorem.

After Fermat, such great minds as Leonhard Euler worked on the search for a proof (in 1770 he proposed a solution for n = 3),

Adrien Legendre and Johann Dirichlet (these scientists jointly found the proof for n = 5 in 1825), Gabriel Lamé (who found the proof for n = 7) and many others. By the mid-80s of the last century, it became clear that the scientific world was on the way to the final solution of Fermat’s Last Theorem, but only in 1993 mathematicians saw and believed that the three-century epic of searching for a proof of Fermat’s last theorem was practically over.

It is easily shown that it is enough to prove Fermat’s theorem only for simple n: 3, 5, 7, 11, 13, 17, ... For composite n, the proof remains valid. But there are infinitely many prime numbers...

In 1825, using the method of Sophie Germain, female mathematicians, Dirichlet and Legendre independently proved the theorem for n=5. In 1839, using the same method, the Frenchman Gabriel Lame showed the truth of the theorem for n=7. Gradually the theorem was proven for almost all n less than one hundred.

Finally, the German mathematician Ernst Kummer, in a brilliant study, showed that the theorem in general cannot be proven using the methods of mathematics of the 19th century. The Prize of the French Academy of Sciences, established in 1847 for the proof of Fermat's theorem, remained unawarded.

In 1907, the wealthy German industrialist Paul Wolfskehl decided to take his own life because of unrequited love. Like a true German, he set the date and time of suicide: exactly at midnight. On the last day he made a will and wrote letters to friends and relatives. Things ended before midnight. It must be said that Paul was interested in mathematics. Having nothing else to do, he went to the library and began to read Kummer’s famous article. Suddenly it seemed to him that Kummer had made a mistake in his reasoning. Wolfskel began to analyze this part of the article with a pencil in his hands. Midnight has passed, morning has come. The gap in the proof has been filled. And the very reason for suicide now looked completely ridiculous. Paul tore up his farewell letters and rewrote his will.

He soon died of natural causes. The heirs were quite surprised: 100,000 marks (more than 1,000,000 current pounds sterling) were transferred to the account of the Royal Scientific Society of Göttingen, which in the same year announced a competition for the Wolfskehl Prize. 100,000 marks were awarded to the person who proved Fermat's theorem. Not a pfennig was awarded for refuting the theorem...

Most professional mathematicians considered the search for a proof of Fermat's Last Theorem a hopeless task and resolutely refused to waste time on such a useless exercise. But the amateurs had a blast. A few weeks after the announcement, an avalanche of “evidence” hit the University of Göttingen. Professor E.M. Landau, whose responsibility was to analyze the evidence sent, distributed cards to his students:

Dear. . . . . . . .

Thank you for sending me the manuscript with the proof of Fermat’s Last Theorem. The first error is on page ... in line... . Because of it, the entire proof loses its validity.
Professor E. M. Landau

In 1963, Paul Cohen, relying on Gödel's findings, proved the unsolvability of one of Hilbert's twenty-three problems - the continuum hypothesis. What if Fermat's Last Theorem is also undecidable?! But true Great Theorem fanatics were not disappointed at all. The advent of computers suddenly gave mathematicians a new method of proof. After World War II, teams of programmers and mathematicians proved Fermat's Last Theorem for all values ​​of n up to 500, then up to 1,000, and later up to 10,000.

In the 1980s, Samuel Wagstaff raised the limit to 25,000, and in the 1990s, mathematicians declared that Fermat's Last Theorem was true for all values ​​of n up to 4 million. But if you subtract even a trillion trillion from infinity, it will not become smaller. Mathematicians are not convinced by statistics. To prove the Great Theorem meant to prove it for ALL n going to infinity.

In 1954, two young Japanese mathematician friends began researching modular forms. These forms generate series of numbers, each with its own series. By chance, Taniyama compared these series with series generated by elliptic equations. They matched! But modular forms are geometric objects, and elliptic equations are algebraic. No connection has ever been found between such different objects.

However, after careful testing, friends put forward a hypothesis: every elliptic equation has a twin - a modular form, and vice versa. It was this hypothesis that became the foundation of an entire direction in mathematics, but until the Taniyama-Shimura hypothesis was proven, the entire building could collapse at any moment.

In 1984, Gerhard Frey showed that a solution to Fermat's equation, if it exists, can be included in some elliptic equation. Two years later, Professor Ken Ribet proved that this hypothetical equation could not have a counterpart in the modular world. From now on, Fermat's Last Theorem was inextricably linked with the Taniyama-Shimura conjecture. Having proven that any elliptic curve is modular, we conclude that there is no elliptic equation with a solution to Fermat's equation, and Fermat's Last Theorem would be immediately proven. But for thirty years it was not possible to prove the Taniyama-Shimura hypothesis, and there was less and less hope for success.

In 1963, when he was just ten years old, Andrew Wiles was already fascinated by mathematics. When he learned about the Great Theorem, he realized that he could not give up on it. As a schoolboy, student, and graduate student, he prepared himself for this task.

Having learned about Ken Ribet's findings, Wiles plunged headlong into proving the Taniyama-Shimura hypothesis. He decided to work in complete isolation and secrecy. “I realized that everything that had anything to do with Fermat’s Last Theorem arouses too much interest... Too many spectators obviously interfere with the achievement of the goal.” Seven years of hard work paid off, Wiles finally completed the proof of the Taniyama-Shimura conjecture.

In 1993, the English mathematician Andrew Wiles presented to the world his proof of Fermat's Last Theorem (Wiles read his sensational paper at a conference at the Sir Isaac Newton Institute in Cambridge.), work on which lasted more than seven years.

While the hype continued in the press, serious work began to verify the evidence. Every piece of evidence must be carefully examined before the evidence can be considered rigorous and accurate. Wiles spent a restless summer waiting for feedback from reviewers, hoping that he would be able to win their approval. At the end of August, experts found the judgment to be insufficiently substantiated.

It turned out that this decision contains a gross error, although in general it is correct. Wiles did not give up, called on the help of the famous specialist in number theory Richard Taylor, and already in 1994 they published a corrected and expanded proof of the theorem. The most amazing thing is that this work took up as many as 130 (!) pages in the mathematical journal “Annals of Mathematics”. But the story did not end there either - the final point was reached only in the next year, 1995, when the final and “ideal”, from a mathematical point of view, version of the proof was published.

“...half a minute after the start of the festive dinner on the occasion of her birthday, I presented Nadya with the manuscript of the complete proof” (Andrew Wales). Have I not yet said that mathematicians are strange people?

This time there was no doubt about the evidence. Two articles were subjected to the most careful analysis and were published in May 1995 in the Annals of Mathematics.

A lot of time has passed since that moment, but there is still an opinion in society that Fermat’s Last Theorem is unsolvable. But even those who know about the proof found continue to work in this direction - few are satisfied that the Great Theorem requires a solution of 130 pages!

Therefore, now the efforts of many mathematicians (mostly amateurs, not professional scientists) are thrown into the search for a simple and concise proof, but this path, most likely, will not lead anywhere...

source

File FERMA-KDVar © N. M. Koziy, 2008

Certificate of Ukraine No. 27312

BRIEF PROOF OF FERmat's Last Theorem

Fermat's Last Theorem is formulated as follows: Diophantine equation (http://soluvel.okis.ru/evrika.html):

A n + B n = C n * /1/

Where n- a positive integer greater than two has no solution in positive integers A , B , WITH .

PROOF

From the formulation of Fermat’s Last Theorem it follows: if n is a positive integer greater than two, then provided that two of the three numbers A , IN or WITH- positive integers, one of these numbers is not a positive integer.

We construct the proof based on the fundamental theorem of arithmetic, which is called the “uniqueness theorem of factorization” or “theorem of the uniqueness of factorization of composite integers.” Odd and even exponents are possible n . Let's consider both cases.

1. Case one: exponent n - odd number.

In this case, the expression /1/ is transformed according to known formulas as follows:

A n + IN n = WITH n /2/

We believe that A And B– positive integers.

Numbers A , IN And WITH must be mutually prime numbers.

From equation /2/ it follows that for given values ​​of numbers A And B factor ( A + B ) n , WITH.

Let's assume that the number WITH - positive integer. Taking into account the accepted conditions and the fundamental theorem of arithmetic, the condition must be satisfied :

WITH n = A n + B n =(A+B) n ∙ D n , / 3/

where is the factor Dn D

From equation /3/ it follows:

From equation /3/ it also follows that the number [ Cn = A n + Bn ] provided that the number WITH ( A + B ) n. However, it is known that:

A n + Bn < ( A + B ) n /5/

Hence:

- a fractional number less than one. /6/

A fractional number.

n

For odd exponents n >2 number:

< 1- дробное число, не являющееся рациональной дробью.

From the analysis of equation /2/ it follows that for an odd exponent n number:

WITH n = A n + IN n = (A+B)

consists of two specific algebraic factors, and for any value of the exponent n the algebraic factor remains unchanged ( A + B ).

Thus, Fermat's last theorem has no solution in positive integers for odd exponents n >2.

2. Case two: exponent n - even number .

The essence of Fermat's last theorem will not change if we rewrite equation /1/ as follows:

A n = Cn - Bn /7/

In this case, equation /7/ is transformed as follows:

A n = C n - B n = ( WITH +B)∙(C n-1 + C n-2 · B+ C n-3 ∙ B 2 +…+ C ∙ Bn -2 + Bn -1 ). /8/

We accept that WITH And IN- whole numbers.

From equation /8/ it follows that for given values ​​of numbers B And C factor (C+ B ) has the same value for any value of the exponent n , therefore it is a divisor of the number A .

Let's assume that the number A– an integer. Taking into account the accepted conditions and the fundamental theorem of arithmetic, the condition must be satisfied :

A n = C n - Bn =(C+ B ) n ∙ Dn , / 9/

where is the factor Dn must be an integer and therefore the number D must also be an integer.

From equation /9/ it follows:

/10/

From equation /9/ it also follows that the number [ A n = WITH n - Bn ] provided that the number A– an integer, must be divisible by a number (C+ B ) n. However, it is known that:

WITH n - Bn < (С+ B ) n /11/

Hence:

- a fractional number less than one. /12/

A fractional number.

It follows that for an odd value of the exponent n equation /1/ of Fermat's last theorem has no solution in positive integers.

For even exponents n >2 number:

< 1- дробное число, не являющееся рациональной дробью.

Thus, Fermat's last theorem has no solution in positive integers and for even exponents n >2.

The general conclusion follows from the above: equation /1/ of Fermat’s last theorem has no solution in positive integers A, B And WITH provided that the exponent n >2.

ADDITIONAL RATIONALE

In the case where the exponent n – even number, algebraic expression ( Cn - Bn ) decomposes into algebraic factors:

C 2 – B 2 =(C-B) ∙ (C+B); /13/

C 4 – B 4 = ( C-B) ∙ (C+B) (C 2 + B 2);/14/

C 6 – B 6 =(C-B) ∙ (C+B) · (C 2 –CB + B 2) ∙ (C 2 +CB+ B 2) ; /15/

C 8 – B 8= (C-B) ∙ (C+B) ∙ (C 2 + B 2) ∙ (C 4 + B 4)./16/

Let's give examples in numbers.

EXAMPLE 1: B=11; C=35.

C 2 – B 2 = (2 2 ∙ 3) ∙ (2 23) = 2 4 3 23;

C 4 – B 4 = (2 2 ∙ 3) ∙ (2 23) (2 673) = 2 4 3 23 673;

C 6 – B 6 = (2 2 ∙ 3) ∙ (2 · 23) · (31 2) · (3 · 577) =2 ∙ 3 ​​∙ 23 ∙ 31 2 ∙ 577;

C 8 – B 8 = (2 2 ∙ 3) ∙ (2 23) (2 673) ∙ (2 75633) = 2 5 ∙ 3 ∙ 23 ∙673 ∙ 75633 .

EXAMPLE 2: B=16; C=25.

C 2 – B 2 = (3 2) ∙ (41) = 3 2 ∙ 41;

C 4 – B 4 = (3 2) ∙ (41) · (881) =3 2 ∙ 41 · 881;

C 6 – B 6 = (3 2) ∙ (41) ∙ (2 2 ∙ 3) ∙ (13 37) (3 ∙ 7 61) = 3 3 7 ∙ 13 37 ∙ 41 ∙ 61;

C 8 – B 8 = (3 2) ∙ (41) ∙ (881) ∙ (17 26833) = 3 2 ∙ 41 ∙ 881 ∙ 17 26833.

From the analysis of equations /13/, /14/, /15/ and /16/ and the corresponding numerical examples it follows:

For a given exponent n , if it is an even number, the number A n = C n - Bn decomposes into a well-defined number of well-defined algebraic factors;

For any exponent n , if it is an even number, in the algebraic expression ( Cn - Bn ) there are always multipliers ( C - B ) And ( C + B ) ;

Each algebraic factor corresponds to a completely definite numerical factor;

For given numbers IN And WITH numeric factors can be prime numbers or composite numeric factors;

Each composite numeric factor is a product of prime numbers that are partially or completely absent from other composite numeric factors;

The size of prime numbers in the composition of composite numerical factors increases with the increase of these factors;

The largest composite numerical factor corresponding to the largest algebraic factor includes the largest prime number to a power less than the exponent n(most often in the first degree).

CONCLUSIONS: Additional evidence supports the conclusion that Fermat's Last Theorem has no solution in positive integers.

mechanical engineer