Properties of the function greatest and least value. How to find the smallest value of a function

And to solve it you will need minimal knowledge of the topic. Another school year is ending, everyone wants to go on vacation, and in order to bring this moment closer, I will immediately get to the point:

Let's start with the area. The area referred to in the condition is limited closed set of points on a plane. For example, the set of points bounded by a triangle, including the WHOLE triangle (if from borders“prick out” at least one point, then the region will no longer be closed). In practice, there are also areas that are rectangular, circular, and slightly larger. complex shapes. It should be noted that in theory mathematical analysis strict definitions are given limitations, isolation, boundaries, etc., but I think everyone is aware of these concepts on an intuitive level, and now nothing more is needed.

A flat region is standardly denoted by the letter , and, as a rule, is specified analytically - by several equations (not necessarily linear); less often inequalities. Typical verbiage: “closed area bounded by lines.”

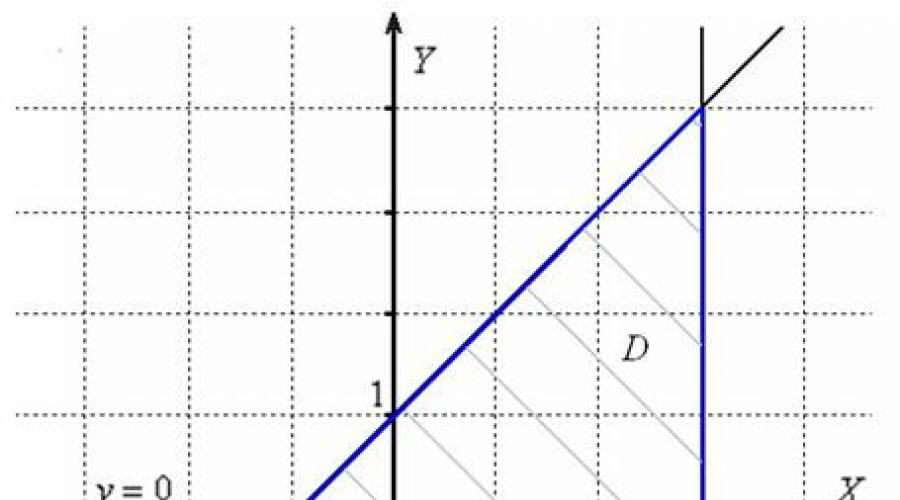
An integral part of the task under consideration is the construction of an area in the drawing. How to do it? You need to draw all the listed lines (in in this case 3 straight) and analyze what happened. The searched area is usually lightly shaded, and its border is marked with a thick line:


The same area can also be set linear inequalities: , which for some reason are often written as an enumerated list rather than system.
Since the boundary belongs to the region, then all inequalities, of course, lax.

And now the essence of the task. Imagine that the axis comes out straight towards you from the origin. Consider a function that continuous in each area point. The graph of this function represents some surface, and the small happiness is that to solve today’s problem we don’t need to know what this surface looks like. It can be located higher, lower, intersect the plane - all this does not matter. And the following is important: according to Weierstrass's theorems, continuous V limited closed area the function reaches its greatest value (the “highest”) and the least (the “lowest”) values ​​that need to be found. Such values ​​are achieved or V stationary points, belonging to the regionD , or at points that lie on the border of this area. This leads to a simple and transparent solution algorithm:

Example 1

In a limited closed area

Solution: First of all, you need to depict the area in the drawing. Unfortunately, it is technically difficult for me to make an interactive model of the problem, and therefore I will immediately present the final illustration, which shows all the “suspicious” points found during the research. They are usually listed one after the other as they are discovered:

Based on the preamble, the decision can be conveniently divided into two points:

I) Find stationary points. This is a standard action that we performed repeatedly in class. about extrema of several variables:

Found stationary point belongs areas: (mark it on the drawing), which means we should calculate the value of the function at a given point:

- as in the article The largest and smallest values ​​of a function on a segment, I will highlight important results in bold. It is convenient to trace them in a notebook with a pencil.

Pay attention to our second happiness - there is no point in checking sufficient condition for an extremum. Why? Even if at a point the function reaches, for example, local minimum, then this DOES NOT MEAN that the resulting value will be minimal throughout the region (see the beginning of the lesson about unconditional extremes) .

What to do if the stationary point does NOT belong to the area? Almost nothing! It should be noted that and move on to the next point.

II) We explore the border of the region.

Since the border consists of the sides of a triangle, it is convenient to divide the study into 3 subsections. But it’s better not to do it anyhow. From my point of view, it is more advantageous to first consider the segments parallel coordinate axes, and first of all, those lying on the axes themselves. To grasp the entire sequence and logic of actions, try to study the ending “in one breath”:

1) Let's deal with the bottom side of the triangle. To do this, substitute directly into the function:

Alternatively, you can do it like this:

Geometrically, this means that the coordinate plane (which is also given by the equation)"carves" out of surfaces a "spatial" parabola, the top of which immediately comes under suspicion. Let's find out where is she located:

– the resulting value “fell” into the area, and it may well turn out that at the point (marked on the drawing) the function reaches the largest or smallest value in the entire region. One way or another, let's do the calculations:

The other “candidates” are, of course, the ends of the segment. Let's calculate the values ​​of the function at points (marked on the drawing):

Here, by the way, you can perform an oral mini-check using a “stripped-down” version:

2) To study the right side of the triangle, substitute it into the function and “put things in order”:

Here we will immediately perform a rough check, “ringing” the already processed end of the segment:
, Great.

The geometric situation is related to the previous point:

– the resulting value also “came into the sphere of our interests,” which means we need to calculate what the function at the appeared point is equal to:

Let's examine the second end of the segment:

Using the function , let's perform a control check:

3) Probably everyone can guess how to explore the remaining side. We substitute it into the function and carry out simplifications:

Ends of the segment have already been researched, but in the draft we still check whether we have found the function correctly :
– coincided with the result of the 1st subparagraph;
– coincided with the result of the 2nd subparagraph.

It remains to find out if there is anything interesting inside the segment:

- There is! Substituting the straight line into the equation, we get the ordinate of this “interestingness”:

We mark a point on the drawing and find the corresponding value of the function:

Let’s check the calculations using the “budget” version :
, order.

And the final step: We CAREFULLY look through all the “bold” numbers, I recommend that beginners even make a single list:

from which we select the largest and smallest values. Answer Let's write down in the style of the problem of finding the largest and smallest values ​​of a function on a segment:

Just in case, I'll comment again geometric meaning result:
– here is the highest point of the surface in the region;
– here is the lowest point of the surface in the area.

In the analyzed task, we identified 7 “suspicious” points, but their number varies from task to task. For a triangular region, the minimum "research set" consists of three points. This happens when the function, for example, specifies plane– it is completely clear that there are no stationary points, and the function can reach its maximum/smallest values ​​only at the vertices of the triangle. But there are only one or two similar examples - usually you have to deal with some surface of 2nd order.

If you try to solve such tasks a little, then the triangles can make your head spin, and that’s why I prepared for you unusual examples so that it becomes square :))

Example 2

Find the largest and smallest values ​​of a function in a closed area bounded by lines

Example 3

Find the largest and smallest values ​​of a function in a limited closed region.

Special attention Pay attention to the rational order and technique of studying the boundary of the region, as well as to the chain of intermediate checks, which will almost completely avoid computational errors. Generally speaking, you can solve it any way you like, but in some problems, for example, in Example 2, there is every chance of making your life much more difficult. Approximate sample finishing assignments at the end of the lesson.

Let’s systematize the solution algorithm, otherwise with my diligence as a spider, it somehow got lost in the long thread of comments of the 1st example:

– At the first step, we build an area, it is advisable to shade it and highlight the border with a bold line. During the solution, points will appear that need to be marked on the drawing.

– Find stationary points and calculate the values ​​of the function only in those of them that belong to the region. We highlight the resulting values ​​in the text (for example, circle them with a pencil). If a stationary point does NOT belong to the region, then we mark this fact with an icon or verbally. If there are no stationary points at all, then we draw a written conclusion that they are absent. In any case, this point cannot be skipped!

– We are exploring the border of the region. First, it is beneficial to understand the straight lines that are parallel to the coordinate axes (if there are any at all). We also highlight the function values ​​calculated at “suspicious” points. A lot has been said above about the solution technique and something else will be said below - read, re-read, delve into it!

– From the selected numbers, select the largest and smallest values ​​and give the answer. Sometimes it happens that a function reaches such values ​​at several points at once - in this case, all these points should be reflected in the answer. Let, for example, and it turned out that it was smallest value. Then we write down that

The final examples are dedicated to others useful ideas which will be useful in practice:

Example 4

Find the largest and smallest values ​​of a function in a closed region .

I have retained the author's formulation, in which the area is given in the form of a double inequality. This condition can be written by an equivalent system or in a more traditional form for this problem:

I remind you that with nonlinear we encountered inequalities on, and if you do not understand the geometric meaning of the notation, then please do not delay and clarify the situation right now;-)

Solution, as always, begins with constructing an area that represents a kind of “sole”:

Hmm, sometimes you have to chew not only the granite of science...

I) Find stationary points:

The system is an idiot's dream :)

A stationary point belongs to the region, namely, lies on its boundary.

And so, it’s okay... the lesson went well - this is what it means to drink the right tea =)

II) We explore the border of the region. Without further ado, let's start with the x-axis:

1) If , then

Let's find where the vertex of the parabola is:
– appreciate such moments – you have “hit” right to the point from which everything is already clear. But we still don’t forget about checking:

Let's calculate the values ​​of the function at the ends of the segment:

2) C bottom Let’s figure out the “bottoms” “in one sitting” - we substitute them into the function without any complexes, and we will only be interested in the segment:

Control:

This already brings some excitement to the monotonous driving along the knurled track. Let's find critical points:

Let's decide quadratic equation, do you remember anything else about this? ...However, remember, of course, otherwise you wouldn’t be reading these lines =) If in the two previous examples calculations in decimals(which, by the way, is rare), then the usual ones await us here common fractions. We find the “X” roots and use the equation to determine the corresponding “game” coordinates of the “candidate” points:


Let's calculate the values ​​of the function at the found points:

Check the function yourself.

Now we carefully study the won trophies and write down answer:

These are “candidates”, these are “candidates”!

To solve it yourself:

Example 5

Find the smallest and largest values ​​of a function in a closed area

An entry with curly braces reads like this: “a set of points such that.”

Sometimes in such examples they use Lagrange multiplier method, But real need it is unlikely to be used. So, for example, if a function with the same area “de” is given, then after substitution into it – with the derivative from no difficulties; Moreover, everything is drawn up in “one line” (with signs) without the need to consider the upper and lower semicircles separately. But, of course, there are more complex cases, where without the Lagrange function (where, for example, is the same equation of a circle) It’s hard to get by – just as it’s hard to get by without a good rest!

Have a good time everyone and see you soon next season!

Solutions and answers:

Example 2: Solution: Let's depict the area in the drawing:

Sometimes in problems B15 there are “bad” functions for which it is difficult to find a derivative. Previously, this only happened during sample tests, but now these tasks are so common that they can no longer be ignored when preparing for the real Unified State Exam.

In this case, other techniques work, one of which is monotone.

A function f (x) is said to be monotonically increasing on the segment if for any points x 1 and x 2 of this segment the following holds:

x 1< x 2 ⇒ f (x 1) < f (x 2).

A function f (x) is said to be monotonically decreasing on the segment if for any points x 1 and x 2 of this segment the following holds:

x 1< x 2 ⇒ f (x 1) > f ( x 2).

In other words, for an increasing function, the larger x, the larger f(x). For a decreasing function the opposite is true: the larger x, the less f(x).

For example, the logarithm increases monotonically if the base a > 1, and monotonically decreases if 0< a < 1. Не забывайте про область acceptable values logarithm: x > 0.

f (x) = log a x (a > 0; a ≠ 1; x > 0)

The arithmetic square (and not only square) root increases monotonically over the entire domain of definition:

The exponential function behaves similarly to the logarithm: it increases for a > 1 and decreases for 0< a < 1. Но в отличие от логарифма, exponential function defined for all numbers, not just x > 0:

f (x) = a x (a > 0)

Finally, degrees with a negative exponent. You can write them as a fraction. They have a break point where the monotony is broken.

All these functions are never found in pure form. They add polynomials, fractions and other nonsense, which makes it difficult to calculate the derivative. Let's look at what happens in this case.

Parabola vertex coordinates

Most often the function argument is replaced with quadratic trinomial of the form y = ax 2 + bx + c. Its graph is a standard parabola in which we are interested in:

1. The branches of a parabola can go up (for a > 0) or down (a< 0). Задают направление, в котором функция может принимать бесконечные значения;
2. The vertex of a parabola is the extremum point of a quadratic function at which this function takes its minimum (for a > 0) or maximum (a< 0) значение.

Of greatest interest is vertex of parabola, the abscissa of which is calculated by the formula:

So, we have found the extremum point of the quadratic function. But if the original function is monotonic, for it the point x 0 will also be an extremum point. Thus, let us formulate the key rule:

Extremum points quadratic trinomial And complex function, which it is included in, coincide. Therefore, you can look for x 0 for a quadratic trinomial, and forget about the function.

From the above reasoning, it remains unclear which point we get: maximum or minimum. However, the tasks are specifically designed so that this does not matter. Judge for yourself:

1. There is no segment in the problem statement. Therefore, there is no need to calculate f(a) and f(b). It remains to consider only the extremum points;
2. But there is only one such point - this is the vertex of the parabola x 0, the coordinates of which are calculated literally orally and without any derivatives.

Thus, solving the problem is greatly simplified and comes down to just two steps:

1. Write out the equation of the parabola y = ax 2 + bx + c and find its vertex using the formula: x 0 = −b /2a ;
2. Find the value of the original function at this point: f (x 0). If there are no additional conditions, this will be the answer.

At first glance, this algorithm and its rationale may seem complicated. I deliberately do not post a “bare” solution diagram, since thoughtless application of such rules is fraught with errors.

Let's look at real problems from trial Unified State Exam in mathematics - this is where this technique is found most often. At the same time, we will make sure that in this way many B15 problems become almost oral.

Under the root stands quadratic function y = x 2 + 6x + 13. The graph of this function is a parabola with branches upward, since the coefficient a = 1 > 0.

Vertex of the parabola:

x 0 = −b /(2a ) = −6/(2 1) = −6/2 = −3

Since the branches of the parabola are directed upward, at the point x 0 = −3 the function y = x 2 + 6x + 13 takes on its minimum value.

The root increases monotonically, which means x 0 is the minimum point of the entire function. We have:

Task. Find the smallest value of the function:

y = log 2 (x 2 + 2x + 9)

Under the logarithm there is again a quadratic function: y = x 2 + 2x + 9. The graph is a parabola with branches up, because a = 1 > 0.

Vertex of the parabola:

x 0 = −b /(2a ) = −2/(2 1) = −2/2 = −1

So, at the point x 0 = −1 the quadratic function takes on its minimum value. But the function y = log 2 x is monotonic, so:

y min = y (−1) = log 2 ((−1) 2 + 2 · (−1) + 9) = ... = log 2 8 = 3

The exponent contains the quadratic function y = 1 − 4x − x 2 . Let's rewrite it in normal form: y = −x 2 − 4x + 1.

Obviously, the graph of this function is a parabola, branches down (a = −1< 0). Поэтому вершина будет точкой максимума:

x 0 = −b /(2a ) = −(−4)/(2 · (−1)) = 4/(−2) = −2

The original function is exponential, it is monotonic, therefore highest value will be at the found point x 0 = −2:

An attentive reader will probably notice that we did not write out the range of permissible values ​​of the root and logarithm. But this was not required: inside there are functions whose values ​​are always positive.

Corollaries from the domain of a function

Sometimes simply finding the vertex of the parabola is not enough to solve Problem B15. The value you are looking for may lie at the end of the segment, and not at all at the extremum point. If the problem does not indicate a segment at all, look at range of acceptable values original function. Namely:

Please note again: zero may well be under the root, but never in the logarithm or denominator of a fraction. Let's see how this works with specific examples:

Task. Find the largest value of the function:

Under the root is again a quadratic function: y = 3 − 2x − x 2 . Its graph is a parabola, but branches down because a = −1< 0. Значит, парабола уходит на минус бесконечность, что недопустимо, поскольку арифметический Square root of a negative number does not exist.

We write out the range of permissible values ​​(APV):

3 − 2x − x 2 ≥ 0 ⇒ x 2 + 2x − 3 ≤ 0 ⇒ (x + 3)(x − 1) ≤ 0 ⇒ x ∈ [−3; 1]

Now let's find the vertex of the parabola:

x 0 = −b /(2a ) = −(−2)/(2 · (−1)) = 2/(−2) = −1

The point x 0 = −1 belongs to the ODZ segment - and this is good. Now we calculate the value of the function at the point x 0, as well as at the ends of the ODZ:

y(−3) = y(1) = 0

So, we got the numbers 2 and 0. We are asked to find the largest - this is the number 2.

Task. Find the smallest value of the function:

y = log 0.5 (6x − x 2 − 5)

Inside the logarithm there is a quadratic function y = 6x − x 2 − 5. This is a parabola with branches down, but in a logarithm there cannot be negative numbers, so we write out the ODZ:

6x − x 2 − 5 > 0 ⇒ x 2 − 6x + 5< 0 ⇒ (x − 1)(x − 5) < 0 ⇒ x ∈ (1; 5)

Please note: the inequality is strict, so the ends do not belong to the ODZ. This differs the logarithm from the root, where the ends of the segment suit us quite well.

We are looking for the vertex of the parabola:

x 0 = −b /(2a ) = −6/(2 · (−1)) = −6/(−2) = 3

The vertex of the parabola fits according to the ODZ: x 0 = 3 ∈ (1; 5). But since we are not interested in the ends of the segment, we calculate the value of the function only at the point x 0:

y min = y (3) = log 0.5 (6 3 − 3 2 − 5) = log 0.5 (18 − 9 − 5) = log 0.5 4 = −2

WITH practical point From a perspective, the greatest interest is in using the derivative to find the largest and smallest values ​​of a function. What is this connected with? Maximizing profits, minimizing costs, determining the optimal load of equipment... In other words, in many areas of life we ​​have to solve problems of optimizing some parameters. And these are the tasks of finding the largest and smallest values ​​of a function.

It should be noted that the largest and smallest values ​​of a function are usually sought on a certain interval X, which is either the entire domain of the function or part of the domain of definition. The interval X itself can be a segment, an open interval , an infinite interval.

In this article we will talk about finding the largest and smallest values ​​explicitly given function one variable y=f(x) .

Page navigation.

The largest and smallest value of a function - definitions, illustrations.

Let's briefly look at the main definitions.

The largest value of the function that for anyone inequality is true.

The smallest value of the function y=f(x) on the interval X is called such a value that for anyone inequality is true.

These definitions are intuitive: the largest (smallest) value of a function is the largest (smallest) accepted value on the interval under consideration at the abscissa.

Stationary points– these are the values ​​of the argument at which the derivative of the function becomes zero.

Why do we need stationary points when finding the largest and smallest values? The answer to this question is given by Fermat's theorem. From this theorem it follows that if a differentiable function has an extremum (local minimum or local maximum) at some point, then this point is stationary. Thus, the function often takes its largest (smallest) value on the interval X at one of the stationary points from this interval.

Also, a function can often take on its largest and smallest values ​​at points at which the first derivative of this function does not exist, and the function itself is defined.

Let’s immediately answer one of the most common questions on this topic: “Is it always possible to determine the largest (smallest) value of a function”? No not always. Sometimes the boundaries of the interval X coincide with the boundaries of the domain of definition of the function, or the interval X is infinite. And some functions at infinity and at the boundaries of the domain of definition can take on both infinitely large and infinitely small values. In these cases, nothing can be said about the largest and smallest value of the function.

For clarity, we will give a graphic illustration. Look at the pictures and a lot will become clearer.

On the segment

In the first figure, the function takes the largest (max y) and smallest (min y) values ​​at stationary points located inside the segment [-6;6].

Consider the case depicted in the second figure. Let's change the segment to . In this example, the smallest value of the function is achieved at a stationary point, and the largest at the point with the abscissa corresponding to the right boundary of the interval.

In Figure 3, the boundary points of the segment [-3;2] are the abscissas of the points corresponding to the largest and smallest value of the function.

On an open interval

In the fourth figure, the function takes the largest (max y) and smallest (min y) values ​​at stationary points located inside the open interval (-6;6).

On the interval , no conclusions can be drawn about the largest value.

At infinity

In the example presented in the seventh figure, the function takes the largest value (max y) at a stationary point with abscissa x=1, and the smallest value (min y) is achieved on the right boundary of the interval. At minus infinity, the function values ​​asymptotically approach y=3.

Over the interval, the function reaches neither the smallest nor the largest value. As x=2 approaches from the right, the function values ​​tend to minus infinity (the line x=2 is a vertical asymptote), and as the abscissa tends to plus infinity, the function values ​​asymptotically approach y=3. A graphic illustration of this example is shown in Figure 8.

Algorithm for finding the largest and smallest values ​​of a continuous function on a segment.

Let us write an algorithm that allows us to find the largest and smallest values ​​of a function on a segment.

1. We find the domain of definition of the function and check whether it contains the entire segment.
2. We find all the points at which the first derivative does not exist and which are contained in the segment (usually such points are found in functions with an argument under the modulus sign and in power functions with a fractional-rational exponent). If there are no such points, then move on to the next point.
3. We determine all stationary points falling within the segment. To do this, we equate it to zero, solve the resulting equation and select suitable roots. If there are no stationary points or none of them fall into the segment, then move on to the next point.
4. We calculate the values ​​of the function at selected stationary points (if any), at points at which the first derivative does not exist (if any), as well as at x=a and x=b.
5. From the obtained values ​​of the function, we select the largest and smallest - they will be the required largest and smallest values ​​of the function, respectively.

Let's analyze the algorithm for solving an example to find the largest and smallest values ​​of a function on a segment.

Example.

Find the largest and smallest value of a function

• on the segment ;
• on the segment [-4;-1] .

Solution.

The domain of definition of a function is the entire set of real numbers, with the exception of zero, that is. Both segments fall within the definition domain.

Find the derivative of the function with respect to:

Obviously, the derivative of the function exists at all points of the segments and [-4;-1].

We determine stationary points from the equation. The only real root is x=2. This stationary point falls into the first segment.

For the first case, we calculate the values ​​of the function at the ends of the segment and at the stationary point, that is, for x=1, x=2 and x=4:

Therefore, the greatest value of the function is achieved at x=1, and the smallest value – at x=2.

For the second case, we calculate the function values ​​only at the ends of the segment [-4;-1] (since it does not contain a single stationary point):

Given a function that is defined and continuous on a certain interval. You need to find the largest (smallest) value of the function on this interval.

Theoretical basis.
Theorem (Second Weierstrass Theorem):

If a function is defined and continuous in a closed interval, then it reaches its maximum and minimum values ​​in this interval.

The function can reach its largest and smallest values ​​either at the internal points of the interval or at its boundaries. Let's illustrate everything possible options.

Explanation:
1) The function reaches its greatest value on the left boundary of the interval at point , and its minimum value on the right boundary of the interval at point .
2) The function reaches its greatest value at the point (this is the maximum point), and its minimum value at the right boundary of the interval at the point.
3) The function reaches its maximum value on the left boundary of the interval at point , and its minimum value at point (this is the minimum point).
4) The function is constant on the interval, i.e. it reaches its minimum and maximum values ​​at any point in the interval, and the minimum and maximum values ​​are equal to each other.
5) The function reaches its greatest value at point , and its minimum value at point (despite the fact that the function has both a maximum and a minimum on this interval).
6) The function reaches its greatest value at a point (this is the maximum point), and its minimum value at a point (this is the minimum point).
Comment:

“Maximum” and “maximum value” are different things. This follows from the definition of maximum and the intuitive understanding of the phrase “maximum value”.

Algorithm for solving problem 2.



4) Select the largest (smallest) from the obtained values ​​and write down the answer.

Example 4:

Determine the largest and smallest value of a function on the segment.
Solution:
1) Find the derivative of the function.

2) Find stationary points (and points suspected of extremum) by solving the equation. Pay attention to the points at which there is no two-sided finite derivative.

3) Calculate the values ​​of the function at stationary points and at the boundaries of the interval.

4) Select the largest (smallest) from the obtained values ​​and write down the answer.

The function on this segment reaches its greatest value at the point with coordinates .

The function on this segment reaches its minimum value at the point with coordinates .

You can verify the correctness of the calculations by looking at the graph of the function under study.


Comment: The function reaches its greatest value at the maximum point, and its minimum at the boundary of the segment.

A special case.

Suppose we need to find the maximum and minimum value some function on an interval. After completing the first point of the algorithm, i.e. calculating the derivative, it becomes clear that, for example, it takes only negative values ​​throughout the entire interval under consideration. Remember that if the derivative is negative, then the function decreases. We found that the function decreases over the entire segment. This situation is shown in graph No. 1 at the beginning of the article.

The function decreases on the segment, i.e. it has no extrema points. From the picture you can see that the function will take the smallest value on the right boundary of the segment, and the largest value on the left. if the derivative on the segment is positive everywhere, then the function increases. The smallest value is on the left border of the segment, the largest is on the right.

In this article I will talk about algorithm for finding the largest and smallest value functions, minimum and maximum points.

From theory it will definitely be useful to us derivative table And differentiation rules. It's all on this plate:

Algorithm for finding the largest and smallest values.

It’s more convenient for me to explain in specific example. Consider:

Example: Find the greatest value of the function y=x^5+20x^3–65x on the segment [–4;0].

Step 1. We take the derivative.

Y" = (x^5+20x^3–65x)" = 5x^4 + 20*3x^2 - 65 = 5x^4 + 60x^2 - 65

Step 2. Finding extremum points.

Extremum point we call those points at which the function reaches its greatest or minimum value.

To find the extremum points, you need to equate the derivative of the function to zero (y" = 0)

5x^4 + 60x^2 - 65 = 0

Now let's solve this bi quadratic equation and the roots found are our extremum points.

I solve such equations by replacing t = x^2, then 5t^2 + 60t - 65 = 0.

Let's reduce the equation by 5, we get: t^2 + 12t - 13 = 0

D = 12^2 - 4*1*(-13) = 196

T_(1) = (-12 + sqrt(196))/2 = (-12 + 14)/2 = 1

T_(2) = (-12 - sqrt(196))/2 = (-12 - 14)/2 = -13

We make the reverse change x^2 = t:

X_(1 and 2) = ±sqrt(1) = ±1
x_(3 and 4) = ±sqrt(-13) (we exclude, there cannot be negative numbers under the root, unless of course we are talking about complex numbers)

Total: x_(1) = 1 and x_(2) = -1 - these are our extremum points.

Step 3. Determine the largest and smallest value.

Substitution method.

In the condition, we were given the segment [b][–4;0]. The point x=1 is not included in this segment. So we are not considering it. But in addition to the point x=-1, we also need to consider the left and right boundaries of our segment, that is, points -4 and 0. To do this, we substitute all these three points into the original function. Note that the original one is the one given in the condition (y=x^5+20x^3–65x), some people begin to substitute it into the derivative...

Y(-1) = (-1)^5 + 20*(-1)^3 - 65*(-1) = -1 - 20 + 65 = [b]44
y(0) = (0)^5 + 20*(0)^3 - 65*(0) = 0
y(-4) = (-4)^5 + 20*(-4)^3 - 65*(-4) = -1024 - 1280 + 260 = -2044

This means that the greatest value of the function is [b]44 and it is achieved at point [b]-1, which is called the maximum point of the function on the segment [-4; 0].

We decided and received an answer, we are great, you can relax. But stop! Don't you think that calculating y(-4) is somehow too difficult? In conditions of limited time, it is better to use another method, I call it this:

Through intervals of sign constancy.

These intervals are found for the derivative of the function, that is, for our biquadratic equation.

I do it like this. I draw a directed segment. I place the points: -4, -1, 0, 1. Despite the fact that 1 is not included in the given segment, it should still be noted in order to correctly determine the intervals of constancy of sign. Let's take some number many times larger than 1, say 100, and mentally substitute it into our biquadratic equation 5(100)^4 + 60(100)^2 - 65. Even without counting anything, it becomes obvious that at point 100 the function has plus sign. This means that for intervals from 1 to 100 it has a plus sign. When passing through 1 (we go from right to left), the function will change sign to minus. When passing through point 0, the function will retain its sign, since this is only the boundary of the segment, and not the root of the equation. When passing through -1, the function will again change sign to plus.

From theory we know that where the derivative of the function is (and we drew this precisely for it) changes sign from plus to minus (point -1 in our case) function reaches its local maximum (y(-1)=44, as calculated earlier) on this segment (this is logically very understandable, the function stopped increasing because it reached its maximum and began to decrease).

Accordingly, where the derivative of the function changes sign from minus to plus, is achieved local minimum of a function. Yes, yes, we also found the local minimum point is 1, and y(1) is the minimum value of the function on the segment, say from -1 to +∞. Please note that this is only a LOCAL MINIMUM, that is, a minimum on a certain segment. Since the real (global) minimum of the function will reach somewhere there, at -∞.

In my opinion, the first method is simpler theoretically, and the second is simpler from the point of view of arithmetic operations, but much more complex from the point of view of theory. After all, sometimes there are cases when the function does not change sign when passing through the root of the equation, and in general you can get confused with these local, global maxima and minima, although you will have to master this well anyway if you plan to enter a technical university (and for why else take the profile Unified State Exam and solve this task). But practice and only practice will teach you to solve such problems once and for all. And you can train on our website. Here .

If you have any questions or something is unclear, be sure to ask. I will be happy to answer you and make changes and additions to the article. Remember we are making this site together!