Solving fractional rational equations examples with solutions. How to solve a rational equation
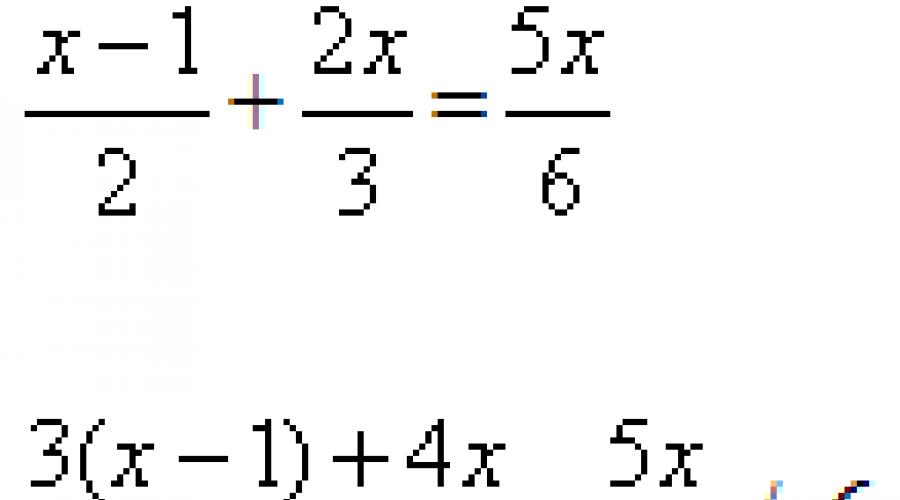
“Rational equations with polynomials” is one of the most frequently encountered topics in test Unified State Exam assignments mathematics. For this reason, they are worth repeating Special attention. Many students are faced with the problem of finding the discriminant, transferring indicators from the right side to the left and bringing the equation to a common denominator, which is why completing such tasks causes difficulties. Solving rational equations in preparation for the Unified State Exam on our website will help you quickly cope with problems of any complexity and pass the test with flying colors.
Choose the Shkolkovo educational portal to successfully prepare for the Unified Mathematics Exam!
To know the rules for calculating unknowns and easily obtain correct results, use our online service. The Shkolkovo portal is a one-of-a-kind platform that contains everything necessary to prepare for Unified State Exam materials. Our teachers systematized and presented in an understandable form all the mathematical rules. In addition, we invite schoolchildren to try their hand at solving standard rational equations, the basis of which is constantly updated and expanded.
For more effective preparation for testing, we recommend following our special method and start by repeating the rules and solutions simple tasks, gradually moving on to more complex ones. Thus, the graduate will be able to identify the most difficult topics for himself and focus on studying them.
Start preparing for the final test with Shkolkovo today, and the results will not be long in coming! Choose the easiest example from those given. If you mastered the expression quickly, move on to more difficult task. This way you can improve your knowledge up to the point of solving USE tasks in mathematics at a specialized level.
Training is available not only to graduates from Moscow, but also to schoolchildren from other cities. Spend a couple of hours a day studying on our portal, for example, and very soon you will be able to cope with equations of any complexity!
An integer expression is a mathematical expression made up of numbers and literal variables using the operations of addition, subtraction and multiplication. Integers also include expressions that involve division by any number other than zero.
The concept of a fractional rational expression
A fractional expression is a mathematical expression that, in addition to the operations of addition, subtraction and multiplication performed with numbers and letter variables, as well as division by a number not equal to zero, also contains division into expressions with letter variables.
Rational expressions are all whole and fractional expressions. Rational equations are equations in which the left and right sides are rational expressions. If in a rational equation the left and right sides are integer expressions, then this rational equation is called an integer.
If in a rational equation the left or right sides are fractional expressions, then such a rational equation is called fractional.
Examples of fractional rational expressions
1. x-3/x = -6*x+19
2. (x-4)/(2*x+5) = (x+7)/(x-2)
3. (x-3)/(x-5) + 1/x = (x+5)/(x*(x-5))
Scheme for solving a fractional rational equation
1. Find common denominator all the fractions that go into the equation.
2. Multiply both sides of the equation by a common denominator.
3. Solve the resulting whole equation.
4. Check the roots and exclude those that make the common denominator vanish.
Since we are solving fractional rational equations, there will be variables in the denominators of the fractions. This means that they will be a common denominator. And in the second point of the algorithm we multiply by a common denominator, then extraneous roots may appear. At which the common denominator will be equal to zero, which means multiplying by it will be meaningless. Therefore, at the end it is necessary to check the obtained roots.
Let's look at an example:
Solve the fractional rational equation: (x-3)/(x-5) + 1/x = (x+5)/(x*(x-5)).
We will stick to general scheme: Let's first find the common denominator of all fractions. We get x*(x-5).
Multiply each fraction by a common denominator and write the resulting whole equation.
(x-3)/(x-5) * (x*(x-5))= x*(x+3);
1/x * (x*(x-5)) = (x-5);
(x+5)/(x*(x-5)) * (x*(x-5)) = (x+5);
x*(x+3) + (x-5) = (x+5);
Let us simplify the resulting equation. We get:
x^2+3*x + x-5 - x - 5 =0;
x^2+3*x-10=0;
We get a simple reduced quadratic equation. We solve it with any of known methods, we get the roots x=-2 and x=5.
Now we check the obtained solutions:
Substitute the numbers -2 and 5 into the common denominator. At x=-2, the common denominator x*(x-5) does not vanish, -2*(-2-5)=14. This means that the number -2 will be the root of the original fractional rational equation.
At x=5 the common denominator x*(x-5) becomes zero. Therefore, this number is not the root of the original fractional rational equation, since there will be a division by zero.
Let's get acquainted with rational and fractional rational equations, give their definition, give examples, and also analyze the most common types of problems.
Yandex.RTB R-A-339285-1
Rational equation: definition and examples
Acquaintance with rational expressions begins in the 8th grade of school. At this time, in algebra lessons, students increasingly begin to encounter assignments with equations that contain rational expressions in their notes. Let's refresh our memory on what it is.
Definition 1
Rational equation is an equation in which both sides contain rational expressions.
In various manuals you can find another formulation.
Definition 2
Rational equation is an equation whose left-hand side contains rational expression, and the right one is zero.
The definitions that we gave for rational equations are equivalent, since they talk about the same thing. The correctness of our words is confirmed by the fact that for any rational expressions P And Q equations P = Q And P − Q = 0 will be equivalent expressions.
Now let's look at the examples.
Example 1
Rational equations:
x = 1 , 2 x − 12 x 2 y z 3 = 0 , x x 2 + 3 x - 1 = 2 + 2 7 x - a (x + 2) , 1 2 + 3 4 - 12 x - 1 = 3 .
Rational equations, just like equations of other types, can contain any number of variables from 1 to several. First we'll look at simple examples, in which the equations will contain only one variable. And then we will begin to gradually complicate the task.
Rational equations are divided into two large groups: integer and fractional. Let's see what equations will apply to each of the groups.
Definition 3
A rational equation will be integer if its left and right sides contain entire rational expressions.
Definition 4
A rational equation will be fractional if one or both of its parts contain a fraction.
Fractional rational equations necessarily contain division by a variable or the variable is present in the denominator. There is no such division in the writing of whole equations.
Example 2
3 x + 2 = 0 And (x + y) · (3 · x 2 − 1) + x = − y + 0, 5– entire rational equations. Here both sides of the equation are represented by integer expressions.
1 x - 1 = x 3 and x: (5 x 3 + y 2) = 3: (x − 1) : 5 are fractionally rational equations.
Whole rational equations include linear and quadratic equations.
Solving whole equations
Solving such equations usually comes down to converting them into equivalent algebraic equations. This can be achieved by carrying out equivalent transformations of equations in accordance with the following algorithm:
- first we get zero on the right side of the equation, for this we need to transfer the expression that is on the right side of the equation to its left side and change the sign;
- then we transform the expression on the left side of the equation into a polynomial standard view.
We must obtain an algebraic equation. This equation will be equivalent to the original equation. Easy cases allow us to reduce the whole equation to a linear or quadratic one to solve the problem. In general, we solve an algebraic equation of degree n.
Example 3
It is necessary to find the roots of the whole equation 3 (x + 1) (x − 3) = x (2 x − 1) − 3.
Solution
Let us transform the original expression in order to obtain an equivalent algebraic equation. To do this, we will transfer the expression contained on the right side of the equation to the left side and replace the sign with the opposite one. As a result we get: 3 (x + 1) (x − 3) − x (2 x − 1) + 3 = 0.
Now let's transform the expression that is on the left side into a standard form polynomial and perform the necessary actions with this polynomial:
3 (x + 1) (x − 3) − x (2 x − 1) + 3 = (3 x + 3) (x − 3) − 2 x 2 + x + 3 = = 3 x 2 − 9 x + 3 x − 9 − 2 x 2 + x + 3 = x 2 − 5 x − 6
We managed to reduce the solution of the original equation to the solution of a quadratic equation of the form x 2 − 5 x − 6 = 0. The discriminant of this equation is positive: D = (− 5) 2 − 4 · 1 · (− 6) = 25 + 24 = 49 . This means there will be two real roots. Let's find them using the formula for the roots of a quadratic equation:
x = - - 5 ± 49 2 1,
x 1 = 5 + 7 2 or x 2 = 5 - 7 2,
x 1 = 6 or x 2 = - 1
Let's check the correctness of the roots of the equation that we found during the solution. For this, we substitute the numbers we received into the original equation: 3 (6 + 1) (6 − 3) = 6 (2 6 − 1) − 3 And 3 · (− 1 + 1) · (− 1 − 3) = (− 1) · (2 · (− 1) − 1) − 3. In the first case 63 = 63 , in the second 0 = 0 . Roots x = 6 And x = − 1 are indeed the roots of the equation given in the example condition.
Answer: 6 , − 1 .
Let's look at what "degree of an entire equation" means. We will often encounter this term in cases where we need to represent an entire equation in algebraic form. Let's define the concept.
Definition 5
Degree of the whole equation is the degree of an algebraic equation equivalent to the original integer equation.
If you look at the equations from the example above, you can establish: the degree of this whole equation is second.
If our course was limited to solving equations of the second degree, then the discussion of the topic could end there. But it's not that simple. Solving equations of the third degree is fraught with difficulties. And for equations higher than the fourth degree there is no general formulas roots. In this regard, solving entire equations of the third, fourth and other degrees requires us to use a number of other techniques and methods.
The most commonly used approach to solving entire rational equations is based on the factorization method. The algorithm of actions in this case is as follows:
- we move the expression from the right side to the left so that zero remains on the right side of the record;
- We represent the expression on the left side as a product of factors, and then move on to a set of several simpler equations.
Find the solution to the equation (x 2 − 1) · (x 2 − 10 · x + 13) = 2 · x · (x 2 − 10 · x + 13) .
Solution
We move the expression from the right side of the record to the left with opposite sign: (x 2 − 1) · (x 2 − 10 · x + 13) − 2 · x · (x 2 − 10 · x + 13) = 0. Transforming the left-hand side into a polynomial of the standard form is inappropriate due to the fact that this will give us an algebraic equation of the fourth degree: x 4 − 12 x 3 + 32 x 2 − 16 x − 13 = 0. The ease of conversion does not justify all the difficulties in solving such an equation.
It’s much easier to go the other way: let’s take the common factor out of brackets x 2 − 10 x + 13 . So we arrive at an equation of the form (x 2 − 10 x + 13) (x 2 − 2 x − 1) = 0. Now let’s replace the resulting equation with a set of two quadratic equations x 2 − 10 x + 13 = 0 And x 2 − 2 x − 1 = 0 and find their roots through the discriminant: 5 + 2 3, 5 - 2 3, 1 + 2, 1 - 2.
Answer: 5 + 2 3, 5 - 2 3, 1 + 2, 1 - 2.
In the same way, we can use the method of introducing a new variable. This method allows us to move to equivalent equations with degrees lower than the degrees in the original integer equation.
Example 5
Does the equation have roots? (x 2 + 3 x + 1) 2 + 10 = − 2 (x 2 + 3 x − 4)?
Solution
If we now try to reduce an entire rational equation to an algebraic one, we will get an equation of degree 4 that has no rational roots. Therefore, it will be easier for us to go the other way: introduce a new variable y, which will replace the expression in the equation x 2 + 3 x.
Now we will work with the whole equation (y + 1) 2 + 10 = − 2 · (y − 4). Let's move the right side of the equation to the left with the opposite sign and carry out the necessary transformations. We get: y 2 + 4 y + 3 = 0. Let's find the roots of the quadratic equation: y = − 1 And y = − 3.
Now let's do the reverse replacement. We get two equations x 2 + 3 x = − 1 And x 2 + 3 · x = − 3 . Let's rewrite them as x 2 + 3 x + 1 = 0 and x 2 + 3 x + 3 = 0. We use the formula for the roots of a quadratic equation in order to find the roots of the first equation from those obtained: - 3 ± 5 2. The discriminant of the second equation is negative. This means that the second equation has no real roots.
Answer:- 3 ± 5 2
Whole equations high degrees come across in tasks quite often. There is no need to be afraid of them. You need to be ready to apply non-standard method their solutions, including a number of artificial transformations.
Solving fractional rational equations
We will begin our consideration of this subtopic with an algorithm for solving fractionally rational equations of the form p (x) q (x) = 0, where p(x) And q(x)– whole rational expressions. The solution of other fractionally rational equations can always be reduced to the solution of equations of the indicated type.
The most commonly used method for solving the equations p (x) q (x) = 0 is based on the following statement: numerical fraction u v, Where v- this is a number that is different from zero, equal to zero only in those cases when the numerator of the fraction is equal to zero. Following the logic of the above statement, we can claim that the solution to the equation p (x) q (x) = 0 can be reduced to fulfilling two conditions: p(x)=0 And q(x) ≠ 0. This is the basis for constructing an algorithm for solving fractional rational equations of the form p (x) q (x) = 0:
- find the solution to the whole rational equation p(x)=0;
- we check whether the condition is satisfied for the roots found during the solution q(x) ≠ 0.
If this condition is met, then the found root. If not, then the root is not a solution to the problem.
Example 6
Let's find the roots of the equation 3 x - 2 5 x 2 - 2 = 0.
Solution
We are dealing with a fractional rational equation of the form p (x) q (x) = 0, in which p (x) = 3 x − 2, q (x) = 5 x 2 − 2 = 0. Let's start solving the linear equation 3 x − 2 = 0. The root of this equation will be x = 2 3.
Let's check the found root to see if it satisfies the condition 5 x 2 − 2 ≠ 0. To do this, substitute a numerical value into the expression. We get: 5 · 2 3 2 - 2 = 5 · 4 9 - 2 = 20 9 - 2 = 2 9 ≠ 0.
The condition is met. It means that x = 2 3 is the root of the original equation.
Answer: 2 3 .
There is another option for solving fractional rational equations p (x) q (x) = 0. Recall that this equation is equivalent to the whole equation p(x)=0 in the region acceptable values variable x of the original equation. This allows us to use the following algorithm in solving the equations p (x) q (x) = 0:
- solve the equation p(x)=0;
- find the range of permissible values of the variable x;
- we take the roots that lie in the range of permissible values of the variable x as the desired roots of the original fractional rational equation.
Solve the equation x 2 - 2 x - 11 x 2 + 3 x = 0.
Solution
First, let's solve the quadratic equation x 2 − 2 x − 11 = 0. To calculate its roots, we use the roots formula for the even second coefficient. We get D 1 = (− 1) 2 − 1 · (− 11) = 12, and x = 1 ± 2 3 .
Now we can find the ODZ of variable x for the original equation. These are all the numbers for which x 2 + 3 x ≠ 0. It's the same as x (x + 3) ≠ 0, from where x ≠ 0, x ≠ − 3.
Now let’s check whether the roots x = 1 ± 2 3 obtained at the first stage of the solution are within the range of permissible values of the variable x. We see them coming in. This means that the original fractional rational equation has two roots x = 1 ± 2 3.
Answer: x = 1 ± 2 3
The second solution method described easier than the first in cases where the range of permissible values of the variable x is easily found, and the roots of the equation p(x)=0 irrational. For example, 7 ± 4 · 26 9. The roots can be rational, but with a large numerator or denominator. For example, 127 1101 And − 31 59 . This saves time on checking the condition q(x) ≠ 0: It is much easier to exclude roots that are not suitable according to the ODZ.
In cases where the roots of the equation p(x)=0 are integers, it is more expedient to use the first of the described algorithms for solving equations of the form p (x) q (x) = 0. Find the roots of an entire equation faster p(x)=0, and then check whether the condition is satisfied for them q(x) ≠ 0, rather than finding the ODZ, and then solving the equation p(x)=0 on this ODZ. This is due to the fact that in such cases it is usually easier to check than to find the DZ.
Example 8
Find the roots of the equation (2 x - 1) (x - 6) (x 2 - 5 x + 14) (x + 1) x 5 - 15 x 4 + 57 x 3 - 13 x 2 + 26 x + 112 = 0.
Solution
Let's start by looking at the whole equation (2 x − 1) (x − 6) (x 2 − 5 x + 14) (x + 1) = 0 and finding its roots. To do this, we apply the method of solving equations through factorization. It turns out that the original equation is equivalent to a set of four equations 2 x − 1 = 0, x − 6 = 0, x 2 − 5 x + 14 = 0, x + 1 = 0, of which three are linear and one is quadratic. Finding roots: from the first equation x = 1 2, from the second – x = 6, from the third – x = 7 , x = − 2 , from the fourth – x = − 1.
Let's check the obtained roots. Determine ADL in in this case It’s difficult for us, since for this we will have to solve an algebraic equation of the fifth degree. It will be easier to check the condition according to which the denominator of the fraction, which is on the left side of the equation, should not go to zero.
Let’s take turns substituting the roots for the variable x in the expression x 5 − 15 x 4 + 57 x 3 − 13 x 2 + 26 x + 112 and calculate its value:
1 2 5 − 15 1 2 4 + 57 1 2 3 − 13 1 2 2 + 26 1 2 + 112 = = 1 32 − 15 16 + 57 8 − 13 4 + 13 + 112 = 122 + 1 32 ≠ 0 ;
6 5 − 15 · 6 4 + 57 · 6 3 − 13 · 6 2 + 26 · 6 + 112 = 448 ≠ 0 ;
7 5 − 15 · 7 4 + 57 · 7 3 − 13 · 7 2 + 26 · 7 + 112 = 0 ;
(− 2) 5 − 15 · (− 2) 4 + 57 · (− 2) 3 − 13 · (− 2) 2 + 26 · (− 2) + 112 = − 720 ≠ 0 ;
(− 1) 5 − 15 · (− 1) 4 + 57 · (− 1) 3 − 13 · (− 1) 2 + 26 · (− 1) + 112 = 0 .
The verification carried out allows us to establish that the roots of the original fractional rational equation are 1 2, 6 and − 2 .
Answer: 1 2 , 6 , - 2
Example 9
Find the roots of the fractional rational equation 5 x 2 - 7 x - 1 x - 2 x 2 + 5 x - 14 = 0.
Solution
Let's start working with the equation (5 x 2 − 7 x − 1) (x − 2) = 0. Let's find its roots. It’s easier for us to imagine this equation as a set of quadratic and linear equations 5 x 2 − 7 x − 1 = 0 And x − 2 = 0.
We use the formula for the roots of a quadratic equation to find the roots. We obtain from the first equation two roots x = 7 ± 69 10, and from the second x = 2.
It will be quite difficult for us to substitute the value of the roots into the original equation to check the conditions. It will be easier to determine the ODZ of the variable x. In this case, the ODZ of the variable x is all numbers except those for which the condition is met x 2 + 5 x − 14 = 0. We get: x ∈ - ∞, - 7 ∪ - 7, 2 ∪ 2, + ∞.
Now let's check whether the roots we found belong to the range of permissible values of the variable x.
The roots x = 7 ± 69 10 belong, therefore, they are the roots of the original equation, and x = 2- does not belong, therefore, it is an extraneous root.
Answer: x = 7 ± 69 10 .
Let us examine separately the cases when the numerator of a fractional rational equation of the form p (x) q (x) = 0 contains a number. In such cases, if the numerator contains a number other than zero, then the equation will have no roots. If this number is equal to zero, then the root of the equation will be any number from the ODZ.
Example 10
Solve the fractional rational equation - 3, 2 x 3 + 27 = 0.
Solution
This equation will not have roots, since the numerator of the fraction on the left side of the equation contains a non-zero number. This means that at no value of x will the value of the fraction given in the problem statement be equal to zero.
Answer: no roots.
Example 11
Solve the equation 0 x 4 + 5 x 3 = 0.
Solution
Since the numerator of the fraction contains zero, the solution to the equation will be any value x from the ODZ of the variable x.
Now let's define the ODZ. It will include all values of x for which x 4 + 5 x 3 ≠ 0. Solutions to the equation x 4 + 5 x 3 = 0 are 0 And − 5 , since this equation is equivalent to the equation x 3 (x + 5) = 0, and this in turn is equivalent to the combination of two equations x 3 = 0 and x + 5 = 0, where these roots are visible. We come to the conclusion that the desired range of acceptable values are any x except x = 0 And x = − 5.
It turns out that the fractional rational equation 0 x 4 + 5 x 3 = 0 has infinite set solutions, which are any numbers except zero and - 5.
Answer: - ∞ , - 5 ∪ (- 5 , 0 ∪ 0 , + ∞
Now let's talk about fractional rational equations of arbitrary form and methods for solving them. They can be written as r(x) = s(x), Where r(x) And s(x)– rational expressions, and at least one of them is fractional. Solving such equations reduces to solving equations of the form p (x) q (x) = 0.
We already know that we can obtain an equivalent equation by transferring an expression from the right side of the equation to the left with the opposite sign. This means that the equation r(x) = s(x) is equivalent to the equation r (x) − s (x) = 0. We have also already discussed ways to convert a rational expression into a rational fraction. Thanks to this, we can easily transform the equation r (x) − s (x) = 0 into an identical rational fraction of the form p (x) q (x) .
So we move from the original fractional rational equation r(x) = s(x) to an equation of the form p (x) q (x) = 0, which we have already learned to solve.
It should be taken into account that when making transitions from r (x) − s (x) = 0 to p(x)q(x) = 0 and then to p(x)=0 we may not take into account the expansion of the range of permissible values of the variable x.
It is quite possible that the original equation r(x) = s(x) and equation p(x)=0 as a result of the transformations they will cease to be equivalent. Then the solution to the equation p(x)=0 can give us roots that will be foreign to r(x) = s(x). In this regard, in each case it is necessary to carry out verification using any of the methods described above.
To make it easier for you to study the topic, we have summarized all the information into an algorithm for solving a fractional rational equation of the form r(x) = s(x):
- we transfer the expression from the right side with the opposite sign and get zero on the right;
- transform the original expression into a rational fraction p (x) q (x) , sequentially performing operations with fractions and polynomials;
- solve the equation p(x)=0;
- We identify extraneous roots by checking their belonging to the ODZ or by substitution into the original equation.
Visually, the chain of actions will look like this:
r (x) = s (x) → r (x) - s (x) = 0 → p (x) q (x) = 0 → p (x) = 0 → elimination EXTERNAL ROOTS
Example 12
Solve the fractional rational equation x x + 1 = 1 x + 1 .
Solution
Let's move on to the equation x x + 1 - 1 x + 1 = 0. Let's transform the fractional rational expression on the left side of the equation to the form p (x) q (x) .
To do this, we will have to reduce rational fractions to a common denominator and simplify the expression:
x x + 1 - 1 x - 1 = x x - 1 (x + 1) - 1 x (x + 1) x (x + 1) = = x 2 - x - 1 - x 2 - x x · (x + 1) = - 2 · x - 1 x · (x + 1)
In order to find the roots of the equation - 2 x - 1 x (x + 1) = 0, we need to solve the equation − 2 x − 1 = 0. We get one root x = - 1 2.
All we have to do is check using any of the methods. Let's look at both of them.
Let's substitute the resulting value into the original equation. We get - 1 2 - 1 2 + 1 = 1 - 1 2 + 1. We have arrived at the correct numerical equality − 1 = − 1 . It means that x = − 1 2 is the root of the original equation.
Now let's check through the ODZ. Let us determine the range of permissible values of the variable x. This will be the entire set of numbers, with the exception of − 1 and 0 (at x = − 1 and x = 0, the denominators of the fractions vanish). The root we obtained x = − 1 2 belongs to ODZ. This means that it is the root of the original equation.
Answer: − 1 2 .
Example 13
Find the roots of the equation x 1 x + 3 - 1 x = - 2 3 · x.
Solution
We are dealing with a fractional rational equation. Therefore, we will act according to the algorithm.
Let's move the expression from the right side to the left with the opposite sign: x 1 x + 3 - 1 x + 2 3 x = 0
Let's carry out the necessary transformations: x 1 x + 3 - 1 x + 2 3 x = x 3 + 2 x 3 = 3 x 3 = x.
We arrive at the equation x = 0. The root of this equation is zero.
Let's check whether this root is extraneous to the original equation. Let's substitute the value into the original equation: 0 1 0 + 3 - 1 0 = - 2 3 · 0. As you can see, the resulting equation makes no sense. This means that 0 is an extraneous root, and the original fractional rational equation has no roots.
Answer: no roots.
If we have not included other equivalent transformations in the algorithm, this does not mean that they cannot be used. The algorithm is universal, but it is designed to help, not limit.
Example 14
Solve the equation 7 + 1 3 + 1 2 + 1 5 - x 2 = 7 7 24
Solution
The easiest way is to solve the given fractional rational equation according to the algorithm. But there is another way. Let's consider it.
Subtract 7 from the right and left sides, we get: 1 3 + 1 2 + 1 5 - x 2 = 7 24.
From this we can conclude that the expression in the denominator on the left side must be equal to the reciprocal of the number on the right side, that is, 3 + 1 2 + 1 5 - x 2 = 24 7.
Subtract 3 from both sides: 1 2 + 1 5 - x 2 = 3 7. By analogy, 2 + 1 5 - x 2 = 7 3, from where 1 5 - x 2 = 1 3, and then 5 - x 2 = 3, x 2 = 2, x = ± 2
Let us carry out a check to determine whether the roots found are the roots of the original equation.
Answer: x = ± 2
If you notice an error in the text, please highlight it and press Ctrl+Enter
"Solving fractional rational equations"
Lesson objectives:
Educational:
- formation of the concept of fractional rational equations; consider various ways to solve fractional rational equations; consider an algorithm for solving fractional rational equations, including the condition that the fraction is equal to zero; teach solving fractional rational equations using an algorithm; checking the level of mastery of the topic by conducting a test.
Developmental:
- developing the ability to correctly operate with acquired knowledge and think logically; development of intellectual skills and mental operations- analysis, synthesis, comparison and synthesis; development of initiative, the ability to make decisions, and not stop there; development critical thinking; development of research skills.
Educating:
- upbringing cognitive interest to the subject; fostering independence in solving educational problems; nurturing will and perseverance to achieve final results.
Lesson type: lesson - explanation of new material.
During the classes
1. Organizational moment.
Hello guys! There are equations written on the board, look at them carefully. Can you solve all of these equations? Which ones are not and why?
Equations in which the left and right sides are fractional rational expressions are called fractional rational equations. What do you think we will study in class today? Formulate the topic of the lesson. So, open your notebooks and write down the topic of the lesson “Solving fractional rational equations.”
2. Updating knowledge. Frontal survey, oral work with the class.
And now we will repeat the main theoretical material that we need to study new topic. Please answer the following questions:
1. What is an equation? ( Equality with a variable or variables.)
2. What is the name of equation No. 1? ( Linear.) Solution linear equations. (Move everything with the unknown to the left side of the equation, all numbers to the right. Give similar terms. Find unknown factor).
3. What is the name of equation No. 3? ( Square.) Methods for solving quadratic equations. ( Isolating a complete square using formulas using Vieta’s theorem and its corollaries.)
4. What is proportion? ( Equality of two ratios.) The main property of proportion. ( If the proportion is correct, then the product of its extreme terms is equal to the product of the middle terms.)
5. What properties are used when solving equations? ( 1. If you move a term in an equation from one part to another, changing its sign, you will get an equation equivalent to the given one. 2. If both sides of the equation are multiplied or divided by the same non-zero number, you get an equation equivalent to the given one.)
6. When does a fraction equal zero? ( A fraction is equal to zero when the numerator is zero and the denominator is not zero..)
3. Explanation of new material.
Solve equation No. 2 in your notebooks and on the board.
Answer: 10.
Which fractional rational equation Can you try to solve using the basic property of proportion? (No. 5).
(x-2)(x-4) = (x+2)(x+3)
x2-4x-2x+8 = x2+3x+2x+6
x2-6x-x2-5x = 6-8
Solve equation No. 4 in your notebooks and on the board.

Answer: 1,5.
What fractional rational equation can you try to solve by multiplying both sides of the equation by the denominator? (No. 6).
![]()
D=1›0, x1=3, x2=4.
Answer: 3;4.
Now try to solve equation number 7 using one of the following methods.

(x2-2x-5)x(x-5)=x(x-5)(x+5) |
|
||
(x2-2x-5)x(x-5)-x(x-5)(x+5)=0 | |||
x(x-5)(x2-2x-5-(x+5))=0 | x2-2x-5-x-5=0 |
||
x(x-5)(x2-3x-10)=0 | |||
x=0 x-5=0 x2-3x-10=0 | |||
x1=0 x2=5 D=49 | |||
Answer: 0;5;-2. | Answer: 5;-2. |
Explain why this happened? Why are there three roots in one case and two in the other? What numbers are the roots of this fractional rational equation?
Until now, students have not encountered the concept of an extraneous root; it is indeed very difficult for them to understand why this happened. If no one in the class can give a clear explanation of this situation, then the teacher asks leading questions.
- How do equations No. 2 and 4 differ from equations No. 5,6,7? ( In equations No. 2 and 4 there are numbers in the denominator, No. 5-7 are expressions with a variable.) What is the root of an equation? ( The value of the variable at which the equation becomes true.) How to find out whether a number is the root of an equation? ( Make a check.)
When testing, some students notice that they have to divide by zero. They conclude that the numbers 0 and 5 are not the roots of this equation. The question arises: is there a way to solve fractional rational equations that allows us to eliminate this error? Yes, this method is based on the condition that the fraction is equal to zero.


x2-3x-10=0, D=49, x1=5, x2=-2.
If x=5, then x(x-5)=0, which means 5 is an extraneous root.
If x=-2, then x(x-5)≠0.
Answer: -2.
Let's try to formulate an algorithm for solving fractional rational equations in this way. Children formulate the algorithm themselves.
Algorithm for solving fractional rational equations:
1. Move everything to the left side.
2. Reduce fractions to a common denominator.
3. Create a system: a fraction is equal to zero when the numerator is equal to zero and the denominator is not equal to zero.
4. Solve the equation.
5. Check the inequality to exclude extraneous roots.
6. Write down the answer.
Discussion: how to formalize the solution if you use the basic property of proportion and multiplying both sides of the equation by a common denominator. (Add to the solution: exclude from its roots those that make the common denominator vanish).
4. Initial comprehension of new material.
Work in pairs. Students choose how to solve the equation themselves depending on the type of equation. Assignments from the textbook “Algebra 8”, 2007: No. 000 (b, c, i); No. 000(a, d, g). The teacher monitors the completion of the task, answers any questions that arise, and provides assistance to low-performing students. Self-test: answers are written on the board.
b) 2 – extraneous root. Answer: 3.
c) 2 – extraneous root. Answer: 1.5.
a) Answer: -12.5.
![]()
g) Answer: 1;1.5.
5. Setting homework.
2. Learn the algorithm for solving fractional rational equations.
3. Solve in notebooks No. 000 (a, d, e); No. 000(g, h).
4. Try to solve No. 000(a) (optional).
6. Completing a control task on the topic studied.
The work is done on pieces of paper.
Example task:

A) Which of the equations are fractional rational?
B) A fraction is equal to zero when the numerator is ______________________ and the denominator is _______________________.
Q) Is the number -3 the root of equation number 6?
D) Solve equation No. 7.
Assessment criteria for the assignment:
- “5” is given if the student completed more than 90% of the task correctly. “4” - 75%-89% “3” - 50%-74% “2” is given to a student who has completed less than 50% of the task. A rating of 2 is not given in the journal, 3 is optional.
7. Reflection.
On the independent work sheets, write:
- 1 – if the lesson was interesting and understandable to you; 2 – interesting, but not clear; 3 – not interesting, but understandable; 4 – not interesting, not clear.
8. Summing up the lesson.
So, today in the lesson we got acquainted with fractional rational equations, learned how to solve these equations different ways, tested their knowledge with the help of a training independent work. You will learn the results of your independent work in the next lesson, and at home you will have the opportunity to consolidate your knowledge.
Which method of solving fractional rational equations, in your opinion, is easier, more accessible, and more rational? Regardless of the method for solving fractional rational equations, what should you remember? What is the “cunning” of fractional rational equations?
Thanks everyone, lesson is over.
In this article I will show you algorithms for solving seven types of rational equations, which can be reduced to quadratic by changing variables. In most cases, the transformations that lead to replacement are very non-trivial, and it is quite difficult to guess about them on your own.
For each type of equation, I will explain how to make a change of variable in it, and then show a detailed solution in the corresponding video tutorial.
You have the opportunity to continue solving the equations yourself, and then check your solution with the video lesson.
So, let's begin.
1 . (x-1)(x-7)(x-4)(x+2)=40
Note that on the left side of the equation there is a product of four brackets, and on the right side there is a number.
1. Let's group the brackets by two so that the sum of the free terms is the same.
2. Multiply them.
3. Let's introduce a change of variable.
In our equation, we will group the first bracket with the third, and the second with the fourth, since (-1)+(-4)=(-7)+2:
![]()
At this point the variable replacement becomes obvious:
We get the equation ![]()
Answer: ![]()
2 .
An equation of this type is similar to the previous one with one difference: on the right side of the equation is the product of the number and . And it is solved in a completely different way:
1. We group the brackets by two so that the product of the free terms is the same.
2. Multiply each pair of brackets.
3. We take x out of each factor.
4. Divide both sides of the equation by .
5. We introduce a change of variable.
In this equation, we group the first bracket with the fourth, and the second with the third, since:
Note that in each bracket the coefficient and the free term are the same. Let's take a factor out of each bracket:
Since x=0 is not a root of the original equation, we divide both sides of the equation by . We get:
![]()
![]()
We get the equation: ![]()
Answer: ![]()
3
. ![]()
Note that the denominators of both fractions are square trinomials, for which the leading coefficient and the free term are the same. Let us take x out of the bracket, as in the equation of the second type. We get:

Divide the numerator and denominator of each fraction by x:

Now we can introduce a variable replacement:
We obtain an equation for the variable t:
4 .
Note that the coefficients of the equation are symmetrical with respect to the central one. This equation is called returnable .
To solve it,
1. Divide both sides of the equation by (We can do this since x=0 is not a root of the equation.) We get:
![]()
2. Let’s group the terms in this way:

3. In each group, let’s take the common factor out of brackets:

4. Let's introduce the replacement:
5. Express through t the expression:
From here ![]()
We get the equation for t:
![]()
Answer:
5. Homogeneous equations.
Equations that have a homogeneous structure can be encountered when solving exponential, logarithmic and trigonometric equations, so you need to be able to recognize it.
Homogeneous equations have the following structure:
In this equality, A, B and C are numbers, and the square and circle denote identical expressions. That is, on the left side of a homogeneous equation there is a sum of monomials having the same degree (in this case, the degree of monomials is 2), and there is no free term.
To solve a homogeneous equation, divide both sides by
Attention! When dividing the right and left sides of an equation by an expression containing an unknown, you can lose roots. Therefore, it is necessary to check whether the roots of the expression by which we divide both sides of the equation are the roots of the original equation.
Let's go the first way. We get the equation:
Now we introduce variable replacement:
Let us simplify the expression and obtain a biquadratic equation for t:
![]()
Answer: or
7
. 
This equation has the following structure:
To solve it, you need to select a complete square on the left side of the equation.
To select a full square, you need to add or subtract twice the product. Then we get the square of the sum or difference. This is crucial for successful variable replacement.
Let's start by finding twice the product. This will be the key to replacing the variable. In our equation, twice the product is equal to
![]()
Now let's figure out what is more convenient for us to have - the square of the sum or the difference. Let's first consider the sum of expressions:
Great! This expression is exactly equal to twice the product. Then, in order to get the square of the sum in brackets, you need to add and subtract the double product:
