Reduction in quantum field theory. Fields and quanta. Problems of quantum field theory

Quantum field theory
Quantum field theory

Quantum field theory (QFT) is a theory of relativistic quantum phenomena that describes elementary particles, their interactions and interconversions based on the fundamental and universal concept of a quantized physical field. QFT is the most fundamental physical theory. Quantum mechanics is a special case of QFT at speeds much lower than the speed of light. Classical field theory follows from QFT if Planck's constant tends to zero.
QFT is based on the idea that all elementary particles are quanta of the corresponding fields. The concept of a quantum field arose as a result of the development of ideas about the classical field and particles and the synthesis of these ideas within the framework of quantum theory. On the one hand, quantum principles led to a revision of classical views of the field as an object continuously distributed in space. The concept of field quanta emerged. On the other hand, a particle in quantum mechanics is associated with a wave function ψ(x,t), which has the meaning of the amplitude of the wave, and the square of the modulus of this amplitude, i.e. magnitude | ψ| 2 gives the probability of detecting a particle at that point in space-time that has coordinates x, t. As a result, a new field was associated with each material particle - the field of probability amplitudes. Thus, fields and particles - fundamentally different objects in classical physics - were replaced by unified physical objects - quantum fields in 4-dimensional space-time, one for each type of particle. Elementary interaction is considered as the interaction of fields at one point or the instantaneous transformation of some particles into others at this point. The quantum field turned out to be the most fundamental and universal form of matter, underlying all its manifestations.

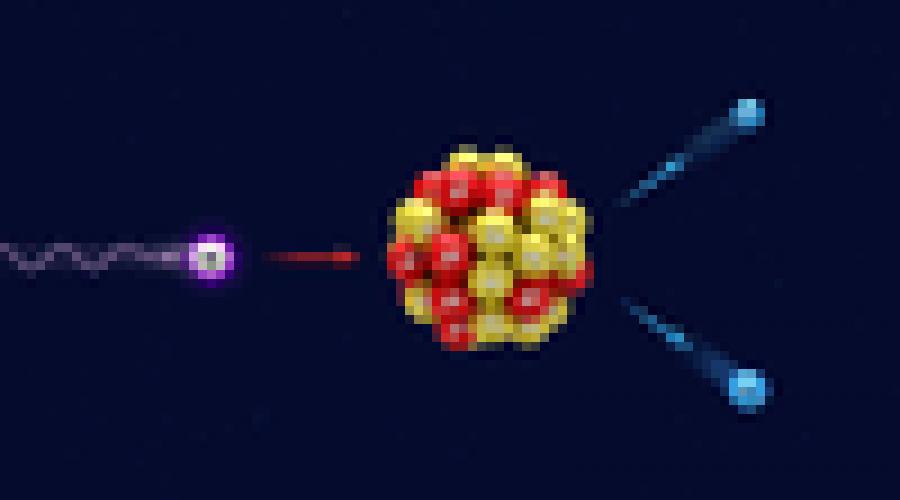
Based on this approach, the scattering of two electrons that have experienced electromagnetic interaction can be described as follows (see figure). In the beginning, there were two free (non-interacting) quanta of the electronic field (two electrons), which moved towards each other. At point 1, one of the electrons released a quantum of the electromagnetic field (photon). At point 2, this quantum of the electromagnetic field was absorbed by another electron. After this, the electrons were removed without interacting. In principle, the QFT apparatus allows one to calculate the probabilities of transitions from an initial set of particles to a given set of final particles under the influence of the interaction between them.
In QFT, the most fundamental (elementary) fields are currently the fields associated with structureless fundamental particles with spin 1/2 - quarks and leptons, and the fields associated with quanta-carriers of the four fundamental interactions, i.e. photon, intermediate bosons, gluons (having spin 1) and graviton (spin 2), which are called fundamental (or gauge) bosons. Despite the fact that fundamental interactions and the corresponding gauge fields have certain common properties, in QFT these interactions are presented within the framework of separate field theories: quantum electrodynamics (QED), electroweak theory or model (ESM), quantum chromodynamics (QCD), and quantum There is no theory of gravitational field yet. So QED is a quantum theory of the electromagnetic field and electron-positron fields and their interactions, as well as electromagnetic interactions of other charged leptons. QCD is a quantum theory of gluon and quark fields and their interactions due to the presence of color charges in them.
The central problem of QFT is the problem of creating a unified theory that unifies all quantum fields.

Quantum mechanics, not to mention quantum field theory, has a reputation for being strange, scary, and counterintuitive. There are those in the scientific community who still do not recognize it. However, quantum field theory is the only theory confirmed by experiment that can explain the interaction of microparticles at low energies. Why is it important? Andrey Kovtun, a student at MIPT and a member of the Department of Fundamental Interactions, tells how to use this theory to get to the main laws of nature or invent them yourself.

As you know, all natural sciences are subject to a certain hierarchy. For example, biology and chemistry have physical foundations. And if we look at the world through a magnifying glass and each time increase its strength, thus reducing knowledge, we will slowly come to quantum field theory. This is a science that describes the properties and interactions of the smallest grains of mother from which we are composed - particles that are commonly called elementary. Some of them - such as the electron, for example - exist on their own, while others combine and form composite particles. The well-known protons and neutrons are just that - they consist of quarks. But quarks themselves are already elementary. So the task of physicists is to understand and deduce all the properties of these particles and answer the question of whether there is something else that lies deeper in the hierarchy of fundamental physical laws.

Our reality is field reality, it consists of fields, and we are only elementary excitations of these fields

For radical scientists, the ultimate goal is a complete reduction of knowledge about the world; for less radical scientists, a deeper penetration into the subtleties of the microworld or supermicroworld. But how is this possible if we are only dealing with particles? The answer is very simple. We simply take them and push them together, literally smash them against each other - like children who, wanting to see the structure of some interesting little thing, simply throw it on the floor and then study the fragments. We also collide particles, and then see which new particles are produced during the collision, and which ones disintegrate after a long journey in splendid isolation. All these processes in quantum theory are described by the so-called decay and scattering probabilities. Quantum field theory deals with calculations of these quantities. But not only them.

Vectors instead of coordinates and velocities

The main difference between quantum mechanics is that we will no longer describe physical bodies using coordinates and velocities. The basic concept in quantum mechanics is the state vector. This is a box containing quantum mechanical information about the physical system we are studying. Moreover, I use the word “system” because a state vector is a thing that can describe the state of both an electron and a grandmother husking sunflower seeds on a bench. That is, this concept has a very wide scope. And we want to find all state vectors that would contain all the information we need about the object under study.

Then it is natural to ask the question “How can we find these vectors and then extract from them what we want?” Here the next important concept of quantum mechanics comes to our aid - the operator. This is a rule according to which one state vector is associated with another. Operators must have certain properties, and some (but not all) of them extract information from state vectors about the physical quantities we need. Such operators are called operators of physical quantities.

Measure what is difficult to measure

Quantum mechanics consistently solves two problems - stationary and evolutionary, and in turn. The essence of the stationary problem is to determine all possible state vectors that can describe a physical system at a given time. Such vectors are the so-called eigenvectors of operators of physical quantities. Having identified them at the initial moment, it is interesting to trace how they will evolve, that is, change over time.

A muon is an unstable elementary particle with a negative electric charge and spin 1⁄2. Antimuon is an antiparticle with quantum numbers (including charge) of the opposite sign, but with equal mass and spin.

Let's look at the evolutionary problem from the point of view of the theory of elementary particles. Suppose we want to collide an electron and its partner - a positron. In other words, we have a state-1 vector that describes an electron-positron pair with certain momenta in the initial state. And then we want to find out with what probability a muon and an antimuon will be born after a collision between an electron and a positron. That is, the system will be described by a state vector, which contains information about the muon and its antipartner, also with certain momenta in the final state. Here's an evolutionary task for you - we want to find out with what probability our quantum system will jump from one state to another.

Let us also solve the problem of the transition of a physical system from state-1 to state-2. Let's say you have a ball. He wants to get from point A to point B, and there are many conceivable ways he could take this journey. But everyday experience shows that if you throw a ball at a certain angle and at a certain speed, then it has only one real path. Quantum mechanics says something else. She says that the ball travels along all these trajectories simultaneously. Each of the trajectories makes its own (more or less) contribution to the probability of transition from one point to another.

Fields

Quantum field theory is so called because it describes not particles themselves, but some more general entities called fields. Particles in quantum field theory are elementary carriers of fields. Imagine the waters of the world's oceans. Let our ocean be calm, nothing is seething on its surface, there are no waves, foam, and so on. Our ocean is a field. Now imagine a solitary wave - just one crest of a wave in the shape of a slide, born as a result of some excitement (for example, hitting the water), which now travels across the vast expanses of the ocean. This is a particle. This analogy illustrates the main idea: particles are elementary excitations of fields. Thus, our reality is field reality, and we consist only of elementary excitations of these fields. Being born from these very fields, their quanta contain all the properties of their ancestors. This is the role of particles in a world in which many oceans called fields simultaneously exist. From a classical point of view, the fields themselves are ordinary numerical functions. They can consist of only one function (scalar fields), or they can consist of many (vector, tensor and spinor fields).

Action

Now it’s time to remember again that each trajectory along which a physical system moves from state-1 to state-2 is formed by a certain probability amplitude. In his works, the American physicist Richard Feynman assumed that the contributions of all trajectories are equal in magnitude, but differ in phase. Simply put, if you have a wave (in this case, a quantum probability wave) traveling from one point to another, the phase (divided by a factor of 2π) shows how many oscillations fit along the way. This phase is a number that is calculated using some rule. And this number is called action.

The basis of the universe, in fact, is the concept of beauty, which is reflected in the term “symmetry”

Associated with action is the basic principle on which all reasonable models that describe physics are now built. This is the principle of least action, and in short, its essence is as follows. Let us have a physical system - it could be either a point or a ball that wants to move from one place to another, or it could be some kind of field configuration that wants to change and become another configuration. They can do this in many ways. For example, a particle tries to get from one point to another in the Earth’s gravitational field, and we see that, in general, there are infinitely many paths along which it can do this. But life suggests that in reality, given the initial conditions, there is only one trajectory that will allow her to get from one point to another. Now - to the essence of the principle of least action. According to a certain rule, we assign a number called an action to each trajectory. Then we compare all these numbers and select only those trajectories for which the action will be minimal (in some cases, maximum). Using this method of choosing paths of least action, you can obtain Newton's laws for classical mechanics or equations describing electricity and magnetism!

There remains a residue because it is not very clear what kind of number this is - an action? If you don’t look too closely, this is some abstract mathematical quantity that, at first glance, has nothing to do with physics - except that it randomly spits out the result we know. In fact, everything is much more interesting. The principle of least action was originally derived from Newton's laws. Then, on its basis, the laws of light propagation were formulated. It can also be obtained from equations describing the laws of electricity and magnetism, and then in the opposite direction - from the principle of least action to arrive at the same laws.

It is remarkable that seemingly different theories acquire the same mathematical formulation. And this leads us to the following assumption: can’t we ourselves come up with some laws of nature using the principle of least action, and then look for them in experiment? We can and we do! This is the meaning of this unnatural and difficult to understand principle. But it works, which makes us think about it precisely as some physical characteristic of the system, and not as an abstract mathematical formulation of modern theoretical science. It is also important to note that we cannot write any actions that our imagination tells us. When trying to figure out what the next physical field theory should look like, we use the symmetries that physical nature has, and along with the fundamental properties of space-time we can use many other interesting symmetries that group theory tells us (a section of general algebra that studies algebraic structures called groups and their properties. - Ed.).

About the beauty of symmetry

It is remarkable that we have received not just a summary of laws describing some natural phenomena, but a way to theoretically obtain laws such as Newton’s or Maxwell’s equations. And although quantum field theory describes elementary particles only at the low energy level, it has already served physicists around the world well and is so far the only theory that sensibly describes the properties of the smallest building blocks that make up our world. What scientists actually want is to write such an action, only quantum, which would contain all possible laws of nature at once. Although even if this were possible, it would not resolve all the questions that interest us.

At the basis of a deep understanding of the laws of nature are some entities that are of a purely mathematical nature. And now, in order to try to penetrate the depths of the universe, we have to abandon high-quality, intuitive arguments. When talking about quantum mechanics and quantum field theory, it is very difficult to find clear and visual analogies, but the most important thing that I would like to convey is that the basis of the universe is, in fact, the concept of beauty, which is reflected in the term “symmetry” " Symmetry is inevitably associated with beauty, as it was, for example, among the ancient Greeks. And it is symmetries, along with the laws of quantum mechanics, that underlie the structure of the smallest bricks in the world that physicists have so far managed to reach.

QUANTUM THEORY

QUANTUM THEORY

theory, the foundations of which were laid in 1900 by physicist Max Planck. According to this theory, atoms always emit or receive radiation energy only in portions, discontinuously, namely in certain quanta (energy quanta), the energy value of which is equal to the oscillation frequency (the speed of light divided by the wavelength) of the corresponding type of radiation, multiplied by the Planck action (see . Constant, Microphysics, and Quantum mechanics). Quantum theory was laid (by Einstein) as the basis for the quantum theory of light (corpuscular theory of light), according to which light also consists of quanta moving at the speed of light (light quanta, photons).

Philosophical Encyclopedic Dictionary. 2010 .

See what "QUANTUM THEORY" is in other dictionaries:

It has the following subsections (the list is incomplete): Quantum mechanics Algebraic quantum theory Quantum field theory Quantum electrodynamics Quantum chromodynamics Quantum thermodynamics Quantum gravity Superstring theory See also... ... Wikipedia

QUANTUM THEORY, a theory that, combined with the theory of RELATIVITY, formed the basis for the development of physics throughout the 20th century. It describes the relationship between MATTER and ENERGY at the level of ELEMENTARY or subatomic PARTICLES, as well as... ... Scientific and technical encyclopedic dictionary

quantum theory- Another way of research is studying the interaction of matter and radiation. The term “quantum” is associated with the name of M. Planck (1858 1947). This is the "black body" problem (an abstract mathematical concept for an object that accumulates all the energy... Western philosophy from its origins to the present day

Unites quantum mechanics, quantum statistics and quantum field theory... Big Encyclopedic Dictionary

Combines quantum mechanics, quantum statistics and quantum field theory. * * * QUANTUM THEORY QUANTUM THEORY combines quantum mechanics (see QUANTUM MECHANICS), quantum statistics (see QUANTUM STATISTICS) and quantum field theory... ... encyclopedic Dictionary

quantum theory- kvantinė teorija statusas T sritis fizika atitikmenys: engl. quantum theory vok. Quantentheorie, f rus. quantum theory, f pranc. théorie des quanta, f; théorie quantique, f … Fizikos terminų žodynas

Phys. a theory that combines quantum mechanics, quantum statistics, and quantum field theory. It is all based on the idea of ​​a discrete (discontinuous) structure of radiation. According to quantum theory, any atomic system can be located in certain... ... Natural science. encyclopedic Dictionary

Quantum field theory is a quantum theory of systems with an infinite number of degrees of freedom (physical fields (See Physical fields)). Quantum mechanics, which arose as a generalization of quantum mechanics (See Quantum mechanics) in connection with the problem of description... ... Great Soviet Encyclopedia

- (QFT), relativistic quantum. theory of physics systems with an infinite number of degrees of freedom. An example of such an electrical system. mag. field, for a complete description of which at any moment in time it is necessary to set the electrical intensities. and mag. fields at each point... Physical encyclopedia

QUANTUM FIELD THEORY. Contents:1. Quantum fields.................. 3002. Free fields and wave-particle duality.................... 3013. Interaction fields.........3024. Perturbation theory............... 3035. Divergences and... ... Physical encyclopedia

Books

• Quantum theory
• Quantum theory, Bohm D.. The book systematically presents non-relativistic quantum mechanics. The author analyzes in detail the physical content and examines in detail the mathematical apparatus of one of the most important...
• Quantum field theory Emergence and development Acquaintance with one of the most mathematized and abstract physical theories Issue 124, Grigoriev V. Quantum theory is the most general and deepest of the physical theories of our time. About how physical ideas about matter changed, how quantum mechanics arose, and then quantum mechanics...

QUANTUM FIELD THEORY.

1. Quantum fields................... 300

2. Free fields and wave-particle duality.................................... 301

3. Interaction of fields.........302

4. Perturbation theory............... 303

5. Divergences and renormalizations......... 304

6. UV asymptotics and renormalization group......... 304

7. Calibration fields........................ 305

8. The big picture............... 307

9. Prospects and problems............ 307

Quantum field theory(QFT) - quantum theory of relativistic systems with an infinitely large number of degrees of freedom (relativistic fields), which is a theoretical the basis for describing microparticles, their interactions and interconversions.

1. Quantum fields Quantum (otherwise quantized) field is a kind of synthesis of classical concepts. fields such as electromagnetic and the probability field of quantum mechanics. According to modern ideas, the quantum field is the most fundamental and universal form of matter, underlying all its specific manifestations. The idea of ​​a classic the field arose in the depths of the Faraday-Maxwell theory of electromagnetism and finally crystallized in the process of creating special. theory of relativity, which required abandoning ether as a material carrier of el-magnetic processes. In this case, the field had to be considered not as a form of movement of the cell. environment, but specific. a form of matter with very unusual properties. Unlike particles, classical the field is continuously created and destroyed (emitted and absorbed by charges), has an infinite number of degrees of freedom and is not localized in a specific way. points of space-time, but can propagate in it, transmitting a signal (interaction) from one particle to another with a finite speed not exceeding With. The emergence of quantum ideas led to a revision of the classical. ideas about the continuity of the emission mechanism and to the conclusion that these processes occur discretely - through the emission and absorption of el-magnetic quanta. fields - photons. Arose contradictory from the point of view of the classical. physics picture when with el-magn. photons were compared by the field and some phenomena could be interpreted only in terms of waves, while others - only with the help of the idea of ​​quanta, called wave-particle duality. This contradiction was resolved subsequently. application of the ideas of quantum mechanics to the field. Dynamic variable el-magn. fields - potentials A , j and electrical tension. and mag. fields E , N - became quantum operators, subject to definitions. commutation relations and acting on the wave function (amplitude, or state vector)systems. Thus, a new physical science arose. object - a quantum field that satisfies the classical equations. , but which has quantum mechanical meanings. operators. The second source of the general concept of a quantum field was the wave function of the particle y ( x, t), edge is not an independent physical entity. magnitude, and the amplitude of the state of the particle: the probabilities of any related to the particle physical. quantities are expressed through expressions that are bilinear in y. Thus, in quantum mechanics, a new field - a field of probability amplitudes - was associated with each material particle. The relativistic generalization of the y-function led P. A. M. Dirac (R. A. M. Dirac) to the four-component wave function of the electron y a (a = 1, 2, 3, 4), transforming according to the spinor representation Lorenz group. It was soon realized that in general every department. a relativistic microparticle should be associated with a local field that implements a certain representation of the Lorentz group and has a physical field. meaning of probability amplitude. Generalization to the plural case. particles showed that if they satisfy the principle of indistinguishability ( identity with the principle), then to describe all particles, one field in four-dimensional space-time is sufficient, which is an operator in the sense of . This is achieved by transition to a new quantum mechanics. representation - representation of filling numbers (or representation of secondary quantization). The operator field introduced in this way turns out to be completely analogous to the quantized electric field. field, differing from it only in the choice of representation of the Lorentz group and, possibly, in the method of quantization. Similar to el-magn. field, one such field corresponds to the entire set of identical particles of a given type, for example, one operator Dirac field describes all the electrons (and positrons!) of the Universe. This is how a universal picture of the uniform structure of all matter arises. To replace the fields and particles of the classical physicists come united physics. objects are quantum fields in four-dimensional space-time, one for each type of particle or (classical) field. The elementary act of any interaction is the interaction of several. fields at one point in space-time, or - in corpuscular language - local and instantaneous transformation of some particles into others. Classic The interaction in the form of forces acting between particles turns out to be a secondary effect resulting from the exchange of quanta of the field carrying the interaction.
2. Free fields and wave-particle duality In accordance with the general physical picture briefly outlined above. picture in a systematic way. The presentation of QFT can be based on both field and corpuscular concepts. In the field approach, one must first construct a theory of the corresponding classical theory. field, then subject it to quantization [on the model of quantization of el-magn. fields by W. Heisenberg and W. Pauli] and, finally, develop a corpuscular interpretation for the resulting quantized field. The main initial concept here will be the field and a(X) (index A numbers the field components) defined at each space-time point x=(ct,x) and carrying out k--l. a fairly simple representation of the Lorentz group. The further theory can be constructed most easily using Lagrangian formalism; choose local [i.e. i.e. depending only on the field components and a(X) and their first derivatives d m and a(X)=du a / dx m = and a m( X) (m=0, 1, 2, 3) at one point X] quadratic Poincare-invariant (see. Poincaré group) Lagrangian L(x) = L(u a , d m u b) and from least action principle obtain the equations of motion. For a quadratic Lagrangian they are linear - free fields satisfy the superposition principle. By virtue of Noether's theorem from the invariance of the action S with respect to each one-parameter. group follows the conservation (independence of time) of one, explicitly indicated by the theorem, integral function of and a And d m u b. Since the Poincaré group itself is 10-parametric, QFT necessarily preserves 10 quantities, which are sometimes called fundams. dynamic quantities: from the invariance with respect to four shifts in four-dimensional space-time, the conservation of four components of the energy-momentum vector follows R m , and from the invariance under six rotations in 4-space it follows that six components of momentum are conserved - three components of three-dimensional angular momentum M i = 1/2 E ijk M jk and three so-called boosts N i =c - l M 0i(i, j, k= 1, 2, 3, E ijk- a single completely antisymmetric tensor; summation is implied over indices occurring twice). With math. point of view ten funds. quantities - R m, M i, N i- essence group generators Poincare. If the action remains invariant even when certain other continuous transformations are performed on the field under consideration that are not included in the Poincaré group - internal transformations. symmetry, - from Noether’s theorem it follows then the existence of new conserved dynamical. quantities Thus, it is often assumed that the field functions are complex and impose the Hermitian condition on the Lagrangian (see. Hermitian operator) and require invariance of the action relative to the global gauge transformation(phase a does not depend on X) and a(X)""e i a and a(X), u*a(X)""e - i a u*a(X). Then it turns out (as a consequence of Noether’s theorem) that the charge is conserved

Therefore, complex functions and a can be used to describe charge. fields. The same goal can be achieved by expanding the range of values ​​covered by the indices A, so that they indicate the direction in the isotopic. space, and requiring the action to be invariant with respect to rotations in it. Note that charge Q is not necessarily electrical. charge, this can be any conserved field characteristic not associated with the Poincaré group, for example, lepton number, strangeness, baryon number and so on. Canonical quantization, according to the general principles of quantum mechanics, is that generalized coordinates [i.e. i.e. (infinite) set of values ​​of all field components u 1 , . . ., u N at all points x space at a certain moment in time t(in a more sophisticated presentation - at all points of a certain spacelike hypersurface s] and generalized impulses p b(x, t)=dL/du b(x, t) are declared to be operators acting on the state amplitude (state vector) of the system, and the commutation relations are imposed on them:

Moreover, the signs “+” or “-” correspond to quantization according to Fermi - Dirac or Bose - Einstein (see below). Here d ab - Kronecker symbol,d( x-y) - delta function Dirac. Due to the highlighted role of time and the inevitable reference to a specific reference system, permutation relations (1) violate the explicit symmetry of space and time, and the preservation of relativistic invariance requires special. proof. In addition, relations (1) do not say anything about commutation. properties of fields in time-like pairs of space-time points - the values ​​of the fields at such points are causally dependent, and their permutations can only be determined by solving the equation of motion together with (1). For free fields, for which the equations of motion are linear, such a problem is solvable in general form and allows us to establish - and, moreover, in a relativistically symmetric form - permutation relations of fields at two arbitrary points X And at.

Here D t - permutation function Pauli - Jordana, satisfying Klein - Gordon's equation Pab- a polynomial that ensures satisfaction of the right-hand side (2) of the equations of motion along X and by at, - D-Alembert operator, t- mass of the field quantum (hereinafter the system of units h= With= 1). In the corpuscular approach to the relativistic quantum description of free particles, the state vectors of the particle must form an irreducible representation of the Poincaré group. The latter is fixed by specifying the values ​​of the Casimir operators (operators that commute with all ten generators of the group R m M i And N i), of which the Poincaré group has two. The first is the squared mass operator m 2 =R m R m. At m 2 No. 0 the second Casimir operator is the square of the ordinary (three-dimensional) spin, and at zero mass - the helicity operator (projection of the spin onto the direction of motion). Range m 2 is continuous - the square of the mass can have any non-negative. meanings, m 20; the spin spectrum is discrete, it can have integer or half-integer values: 0, 1 / 2, 1, ... In addition, it is necessary to specify the behavior of the state vector when reflecting an odd number of coordinate axes. If no other characteristics are required, the particle is said to have no internal properties. degrees of freedom and so-called true neutral particle. Otherwise, the particle has charges of one kind or another. To fix the state of a particle within a representation, in quantum mechanics it is necessary to specify the values ​​of a complete set of commuting operators. The choice of such a set is ambiguous; for a free particle it is convenient to take three components of its momentum R and projection s back l s on k--l. direction. Thus, the state of one free truly neutral particle is completely characterized by specifying the numbers t, l s, р x, p y, р z, s, the first two of which determine the representation, and the next four determine the state in it. For charging more particles will be added; Let's denote them by the letter t. In the representation of occupation numbers, the state of a collection of identical particles is fixed filling numbers n p,s, t of all single-particle states (indices characterizing the representation, in general, are not written out). In turn, the state vector | n p,s, t > is written as the result of the action on the vacuum state |0> (i.e., a state in which there are no particles at all) of creation operators a + (p, s, t):

Birth operators A+ and its Hermitian conjugate annihilation operators A - satisfy the commutation relations

where the signs “+” and “-” correspond, respectively, to Fermi - Dirac and Bose - Einstein quantization, and the occupation numbers are the proper ones. values ​​of the particle number operators Thus, the state vector of a system containing one particle each with quantum numbers p 1 , s 1, t 1; p 2 , s 2, t 2; . . ., written as

To take into account the local properties of the theory, it is necessary to translate the operators a b into a coordinate representation. It is convenient to use the classic ones as transformation functions. solving the equations of motion of a suitable free field with tensor (or spinor) indices A and index internal symmetry q. Then the operators of creation and annihilation in the coordinate representation will be:


These operators, however, are still unsuitable for constructing a local QFT: both their commutator and anticommutator are proportional to the Pauli-Jordan function D t, and its positive and negative frequency parts D 6 m(x-y)[D m =D + m +D - m], which for spacelike pairs of points X And at do not go to zero. To obtain a local field, it is necessary to construct a superposition of the creation and annihilation operators (5). For truly neutral particles this can be done directly by defining the local Lorentz covariant field as
u a(x)=u a(+ ) (X) + and a(-) (X). (6)
But for charging. particles cannot do this: operators a + t and a- t in (6) one will increase and the other will decrease the charge, and their linear combination will not have a definition in this regard. properties. Therefore, to form a local field it is necessary to pair with the creation operators a + t annihilation operators not of the same particles, but of new particles (marked at the top with a “tilde”), implementing the same representation of the Poincaré group, i.e., having exactly the same mass and spin, but differing from the original ones in the charge sign (signs of all charges t), and write:

From Pauli's theorems It now follows that for fields of integer spin, the field functions of which provide a unique representation of the Lorentz group, during Bose-Einstein quantization the commutators [ And(X), And(at)]_ or [ And(X), v*(at)]_ proportional functions D m(x-y) and disappear outside the light cone, while for those implementing two-valued representations of half-integer spin fields the same is achieved for anticommutators [ And(X), And(at)] + (or [ v(x), v* (y)] +) for Fermi-Dirac quantization. The connection expressed by formulas (6) or (7) between Lorentz-covariant field functions satisfying linear equations And or v, v* and operators of creation and destruction of free particles in stationary quantum mechanics. states there is an exact math. description of wave-particle duality. New particles “born” by operators, without which it was impossible to construct local fields (7), are called - in relation to the original ones - antiparticles. The inevitability of the existence of an antiparticle for each charge. particles - one of ch. conclusions of the quantum theory of free fields.
3. Field interaction Solutions (6) and (7) of the free field proportional equations. operators of the creation and annihilation of particles in stationary states, i.e., they can describe only such situations when nothing happens to the particles. In order to also consider cases when some particles influence the motion of others or transform into others, it is necessary to make the equations of motion nonlinear, i.e., to include in the Lagrangian, in addition to terms quadratic in the fields, also terms with higher degrees. From the point of view of the theory developed so far, such interaction Lagrangians L int could be any functions of fields and their first derivatives, satisfying only a number of simple conditions: 1) locality of interaction, requiring that L int(x) depended on diff. fields and a(X) and their first derivatives at only one point in space-time X; 2) relativistic invariance, to fulfill the cut L int must be a scalar with respect to Lorentz transformations; 3) invariance under transformations from internal symmetry groups, if the model under consideration has any. For theories with complex fields, this includes, in particular, the requirements for the Lagrangian to be Hermitian and invariant with respect to gauge transformations admissible in such theories. In addition, one can demand that the theory be invariant under certain discrete transformations, such as spatial inversion P, time reversal T And charge conjugation C(replacing particles with antiparticles). Proven ( CPT theorem), that any interaction that satisfies conditions 1)-3), must necessarily be invariant with respect to the same time. performing these three discrete transformations. The variety of interaction Lagrangians satisfying conditions 1)-3) is as wide as, for example, the variety of Lagrange functions in the classical. mechanics, and on certain At the stage of development of QFT, it seemed that the theory did not answer the question of why exactly some of them, and not others, are realized in nature. However, after the idea arose renormalizations UV divergences (see section 5 below) and its brilliant implementation in quantum electrodynamics(QED) a predominant class of interactions emerged - renormalizable ones. Condition 4) - renormalizability turns out to be very restrictive, and its addition to conditions 1)-3) leaves only interactions with L int the form of polynomials of low degree in the fields under consideration, and fields of any high spins are generally excluded from consideration. Thus, interaction in a renormalizable QFT does not allow - in striking difference from the classical one. and quantum mechanics - no arbitrary functions: as soon as a specific set of fields is chosen, arbitrariness in L int limited to a fixed number interaction constants(coupling constants). A complete system of QFT equations with interaction (in Heisenberg representation) are composed of the equations of motion obtained from the complete Lagrangian (a coupled system of partial differential equations with nonlinear terms of interaction and self-action) and canonical. commutation relations (1). An exact solution to such a problem can be found only in a small number of physically low-containing substances. cases (for example, for certain models in two-dimensional space-time). On the other hand, canon. commutation relations violate, as already mentioned, the obvious relativistic symmetry, which becomes dangerous if, instead of an exact solution, one is content with an approximate one. Therefore, practical the value of quantization in form (1) is small. Naib. a method based on the transition to interaction representation, in which the fields and a(x) satisfy the linear equations of motion for free fields, and all the influence of interaction and self-action is transferred to the time evolution of the amplitude of the state Ф, which is now not constant, but changes in accordance with an equation of the Schrödinger type:

and Hamiltonian interactions H int(t) in this representation depends on time through the fields and a(x), subject to free equations and relativistic-covariant permutation relations (2); Thus, the explicit use of canonical terms turns out to be unnecessary. switches (1) for interacting fields. For comparison with experiment, the theory must solve the problem of particle scattering, in the formulation it is assumed that asymptotically, at t""-:(+:) the system was in a stationary state (will come to a stationary state) Ф_ : (Ф + :), and Ф b: are such that the particles in them do not interact due to large mutual distances (see also Adiabatic hypothesis), so that all mutual influence of particles occurs only at finite times near t = 0 and transforms Ф_ : into Ф + : = S F_: . Operator S called scattering matrix(or S-matrix); through the squares of its matrix elements

the probabilities of transitions from a given beginning are expressed. state F i in some final state F f, i.e. eff. cross sections different processes. That., S-matrix allows you to find the probabilities of physical. processes without delving into the details of the time evolution described by the amplitude Ф( t). Nevertheless S-matrix is ​​usually constructed based on equation (8), which allows a formal solution in a compact form:
.

using the operator T chronological ordering, arranging all field operators in descending order of time t=x 0 (see Chronological work).Expression (10), however, is rather symbolic. recording procedure sequential integration of equation (8) from -: to +: over infinitesimal time intervals ( t, t+D t), rather than a usable solution. This can be seen at least from the fact that for the smooth calculation of matrix elements (9) it is necessary to present the scattering matrix in the form not of chronological, but normal product, in which all creation operators are to the left of destruction operators. The task of transforming one work into another is a true difficulty and cannot be solved in a general form.
4. Perturbation theory For this reason, to constructively solve the problem, one has to resort to the assumption that the interaction is weak, i.e., the interaction Lagrangian is small L int. Then you can decompose chronologically. exponential in expression (10) in a series perturbation theory, and matrix elements (9) will be expressed in each order of perturbation theory through non-chronological matrix elements. exponents, and simple chronological ones. products of the corresponding number of interaction Lagrangians:

(P- the order of perturbation theory), i.e. it will be necessary to transform not exponentials, but simple polynomials of a specific type to normal form. This task is practically accomplished using technology Feynman diagrams and Feynman ruled. In Feynman's technique, each field and a(x) is characterized by its causal Green's function ( propagator or propagation function), D c aa"(x-y), depicted in the diagrams by a line, and each interaction - by a coupling constant and a matrix multiplier from the corresponding term in L int shown in the diagram top. The popularity of the Feynman diagram technique, in addition to ease of use, is due to its clarity. Diagrams allow one to visualize the processes of propagation (lines) and interconversion (vertices) of particles - real in the beginning. and final states and virtual in intermediate states (on internal lines). Particularly simple expressions are obtained for the matrix elements of any process in the lowest order of perturbation theory, which correspond to the so-called. tree diagrams that do not have closed loops - after the transition to the impulse representation, there are no integrations left in them at all. For basic QED processes such expressions for matrix elements were obtained at the dawn of the emergence of QFT in the late 1960s. 20s and turned out to be in reasonable agreement with experiment (the level of agreement is 10 - 2 -10 - 3, i.e., of the order of the fine structure constant a). However, attempts to calculate radiation corrections(i.e., corrections associated with taking into account higher approximations) to these expressions, for example, to Klein - Nishina - Tamm f-le (see. Klein - Nishina formula) for Compton scattering, came across specific. difficulties. Such corrections correspond to diagrams with closed loops of lines virtual particles, the impulses of which are not fixed by conservation laws, and the total correction is equal to the sum of contributions from all possible impulses. It turned out that in most cases, the integrals over the momenta of virtual particles that arise when summing these contributions diverge in the UV region, i.e., the corrections themselves turn out to be not only not small, but infinite. According to the uncertainty relation, large impulses correspond to small distances. Therefore, one might think that physical. The origins of the divergences lie in the idea of ​​the locality of interaction. In this regard, we can talk about an analogy with the infinite energy of el-magn. fields of a point charge in classical. electrodynamics.
5. Divergences and renormalizations Formally, mathematically, the appearance of divergences is due to the fact that propagators Dc(x) are singular (more precisely, generalized) functions that have in the vicinity of the light cone at x 2 ~0 features such as poles and delta functions X 2. Therefore, their products arising in matrix elements, which correspond to closed loops in the diagrams, are poorly defined with mathematics. points of view. The impulse Fourier images of such products may not exist, but - formally - are expressed through divergent impulse integrals. So, for example, the Feynman integral
(Where R- external 4-pulse, k- integration pulse), corresponding to the simplest one-loop diagram with two internal ones. scalar lines (Fig.), does not exist.

He's proportional. Fourier transform of the squared propagator Dc(x) scalar field and diverges logarithmically at the upper limit (i.e. in the UV region of virtual pulses | k|"":, so, for example, if you cut off the integral at the upper limit at | k|=L, then

Where I con ( R) is the final expression.
The problem of UV divergences was solved (at least from the point of view of obtaining final expressions for most physically interesting quantities) in the 2nd half. 40s based on the idea of ​​renormalizations (renormalizations). The essence of the latter is that the infinite effects of quantum fluctuations corresponding to closed loops of diagrams can be isolated into factors that have the nature of corrections to the initial characteristics of the system. As a result, the masses and coupling constants g change due to interaction, i.e. they are renormalized. In this case, due to UV divergences, the renormalizing additives turn out to be infinitely large. Therefore, the renormalization relations

m 0 ""m=m 0 + D m=m 0 Z m (. . .),

g 0 ""g = g 0 +D g = g 0 Z g(. . .)

(Where Z m, Z g- renormalization factors), connecting the original ones, the so-called. seed masses m 0 and seed charges (i.e. coupling constants) g 0 with physical t, g, turn out to be singular. In order not to deal with meaningless endless expressions, one or another auxiliary is introduced. regularization of divergences(similar to the cutoff used in (13) at | k|=L. In the arguments (indicated on the right-hand sides of (14) by ellipses) radiation. amendments D m,D g, as well as renormalization factors Z i, besides T 0 and g 0, contains singular dependencies on the auxiliary parameters. regularization. Elimination of divergences occurs by identifying renormalized masses and charges m And g with their physical values. In practice, to eliminate divergences, the technique of introducing into the original Lagrangian is often used: counter-members and express T 0 and g 0 in the Lagrangian through physical m And g formal relations inverse to (14). Expanding (14) into series according to physics. interaction parameter:

T 0 = T + gM 1 + g 2 M 2 + ..., g 0 = g + g 2 G 1 + g 3 G 2 + ...,

select singular coefficients M l, G l thus, in order to exactly compensate for the divergences arising in the Feynman integrals. A class of QFT models for which such a program can be consistently carried out in all orders of perturbation theory and in which, i.e., without exception, all UV divergences can be “removed” into the renormalization factors of masses and coupling constants, called. class of renormalizable theories. In theories of this class, all matrix elements and Green's functions end up being expressed in a non-singular way through physics. masses, charges and kinematics. variables. In renormalizable models, one can therefore, if desired, completely abstract from the bare parameters and UV divergences, considered separately, and fully characterize the theoretical results. calculations by specifying a finite number of physical values ​​of masses and charges. Math. the basis of this statement is Bogolyubov - Parasyuk theorem on renormalizability. From it follows a fairly simple recipe for obtaining finite unambiguous expressions for matrix elements, formalized in the form of the so-called. R operations Bogolyubova. At the same time, in non-renormalizable models, an example of which is the now obsolete formulation in the form of a four-fermion local Fermi Lagrangian, it is not possible to “collect” all the divergences into “aggregates” that renormalize masses and charges. Renormalizable QFT models are characterized, as a rule, by dimensionless coupling constants, logarithmically divergent contributions to the renormalization of coupling constants and fermion masses, and quadratically divergent radii. corrections to the masses of scalar particles (if any). For such models, as a result of the renormalization procedure we obtain renormalized perturbation theory, edges and serves as the basis for practical. calculations. In renormalizable QFT models, an important role is played by renormalized Green's functions (dressed propagators) and apical parts, including interaction effects. They can be represented by infinite sums of terms corresponding to increasingly complex Feynman diagrams with a fixed number and type of ext. lines. For such quantities one can give formal definitions either through vacuum medium chronological products of field operators in the interaction representation and the S-matrix (which is equivalent to the vacuum averages of the T-products of complete, i.e., Heisenberg, operators), or through functional derivatives of generating functional Z(J), expressed through the so-called extended scattering matrix S( J), functionally dependent on the auxiliary. classic sources J a (x)fields and a(x). The formalism of generating functionals in QFT is an analogue of the corresponding formalism of statistical theory. physics. It allows you to obtain for complete Green functions and vertex functions equations in functional derivatives - Schwinger equations, from which in turn one can obtain an infinite chain of integro-differentials. level - -Dyson equations. The latter are similar to a chain of equations for correlations. statistical functions physics.
6. UV asymptotics and renormalization group High-energy divergences are closely related to UV divergences in QFT. asymptotic behavior of renormalized expressions. For example, logarithmic divergence (12) of the simplest Feynman integral I(p) answers logarithmic. asymptotics

finite regularized integral (13), as well as the corresponding renormalized expression. Since in renormalizable models with dimensionless coupling constants the divergences are mainly logarithmic. character, UV asymptotics l-loop integrals, as a rule (the exception is the case twice logarithmic asymptotics), have a typical structure here ( gL)l, Where L= ln(- R 2/m2), p is a “large” impulse, and m is a certain parameter of the mass dimension that arises in the process of renormalization. Therefore, for sufficiently large values ​​| R 2 | the growth of the logarithm compensates for the smallness of the coupling constant g and the problem arises of determining an arbitrary term of the series of the form

and summing such a series ( a lm- numerical coefficients). Solving these problems is facilitated by using the method renormalization group, which is based on the group nature of finite transformations similar to the singular renormalization functions (14) and the accompanying transformations of the Green functions. In this way, it is possible to effectively sum up certain infinite sets of contributions from Feynman diagrams and, in particular, to represent double expansions (15) in the form of single ones:

where are the functions f l have a characteristic geometric appearance. progression or a combination of a progression with its logarithm and exponent. What turns out to be very important here is this condition for the applicability of a f-l of type (15), which has the form g<<1, gL<< 1, is replaced by a much weaker one: - so-called. invariant charge, which in the simplest (one-loop) approximation has the form of a sum of geoms. progression by argument gL: (b 1 - numerical coefficient). For example, in QED the invariant charge is proportional to the transverse part of the photon propagator d, in the one-loop approximation turns out to be equal

and with k 2 /m 2 >0 L=ln( k 2 /m 2)+ i p( k- 4-pulse of a virtual photon). This is an expression representing the sum of ch. logarithms of the form a(a L)n, has the so-called ghost pole at k 2 = -m 2 e 3 p/a, so called because its position and especially the residue sign contradict a number of general properties of QFT (expressed, for example, spectral representation for photon propagator). The presence of this pole is closely related to the problem of the so-called. zero-charge,T. i.e. the renormalized charge turns to zero at a finite value of the “seed” charge. The difficulty associated with the appearance of the ghost pole has sometimes even been interpreted as evidence of internal. inconsistencies of QED, and the transfer of this result to traditional. renormalizable models of strong interaction of hadrons - as an indication of the inconsistency of the entire local QFT as a whole. However, such cardinal conclusions made on the basis of the chapter. logarithmic the approaches turned out to be hasty. Already taking into account the “following the main” contributions ~a 2 (a L)m, leading to the two-loop approximation, shows that the position of the pole shifts noticeably. A more general analysis within the framework of the renormalization method. group leads to the conclusion that formula (16) is applicable only in the region i.e., the impossibility of proving or disproving the existence of a “pole contradiction” on the basis of one or another resummation of series (15). Thus, the paradox of the phenomenon of a ghostly pole (or the reversal of a renormalized charge to zero) turns out to be illusory - it would be possible to decide whether this difficulty really appears in theory only if we were able to obtain unambiguous results in the region of strong coupling. Until then For now, the only conclusion that remains is that - when applied to spinor QED - perturbation theory is not, despite the unconditional smallness of the expansion parameter a, a logically closed theory. For QED, however, this problem could be considered purely academic, since, according to (16), even at gigantic energies ~(10 15 -10 16) GeV, considered in modern times. models of combining interactions, the condition is not violated. The situation in quantum mesodynamics - the theory of interaction of pseudoscalar meson fields with fermion fields of nucleons, which was presented at the beginning - looked much more serious. 60s unity candidate for the role of a renormalizable model of strong interaction. In it, the effective coupling constant was large at ordinary energies, and the - clearly unauthorized - consideration in perturbation theory led to the same difficulties of the null charge. As a result of all the studies described, a somewhat pessimistic outlook emerged. point of view on the future prospects of renormalizable QFT. Purely theoretical. point of view it seemed that the qualities. the variety of such theories is negligible: for any renormalizable model, all interaction effects - for small coupling constants and moderate energies - were limited to an unobservable change in the characteristics of free particles and the fact that quantum transitions arose between states with such particles, to the probabilities of the lowest approximation of which it was now possible calculate (small) corrections of higher ones. For large coupling constants or asymptotically large energies, the existing theory - again regardless of the specific model - was inapplicable. The only (admittedly brilliant) application to the real world that satisfied these restrictions was QED. This situation contributed to the development of non-Hamiltonian methods (such as axiomatic quantum field theory, algebraic approach in KTP, constructive quantum field theory). Great hopes were placed on dispersion relations method and research analytical. properties of the S-matrix. Mn. researchers began to look for a way out of difficulties along the way of revising the basic principles. provisions of local renormalized QFT with the help of the development of non-canonical. directions: essentially nonlinear (i.e., nonpolynomial), nonlocal, nondefinite (see Nonpolynomial quantum field theories, Nonlocal quantum field theory, Indefinite metric) etc. The source of new views on the general situation in QFT was the discovery of new theoretical theories. facts related to non-Abelian gauge fields. 7. Calibration fields Gauge fields (including non-Abelian Young-Mills field) are associated with invariance with respect to some group G local gauge transformations. The simplest example of a gauge field is an electric magnet. field A m in QED associated with the Abelian group U(l). In the general case of unbroken symmetry, Yang-Mills fields, like a photon, have zero rest mass. They are converted by the attached group representation G, carry the corresponding indices B ab m( x) and obey nonlinear equations of motion (linearizable only for the Abelian group). Their interaction with the fields of matter will be gauge invariant if obtained by extending the derivatives (see. Covariant derivative): in the free Lagrangian of the field and with the same dimensionless constant g, which is included in the Lagrangian of the field IN. Similar to el-magn. field, Yang-Mills fields are systems with connections. This, as well as the apparent absence of massless vector particles (other than photons) in nature, limited interest in such fields, and for more than 10 years they were viewed more as an elegant model with no relation to the real world. The situation changed by the 2nd floor. 60s, when they were able to be quantized using the method of functional integration (see. Functional integral method) and find out that both the pure massless Yang-Mills field and the field interacting with fermions are renormalizable. Following this, a method was proposed for “softly” introducing masses into these fields using the effect spontaneous symmetry breaking. Based on it Higgs mechanism makes it possible to impart mass to quanta of Yang-Mills fields without violating the renormalizability of the model. On this basis, in con. 60s a unified renormalizable theory of the weak and el-magnetic was constructed. interactions (see Electroweak interaction), in which the carriers of weak interaction are heavy (with masses ~ 80-90 GeV) quanta of vector gauge fields of the electroweak symmetry group ( intermediate vector bosons W 6 and Z 0, experimentally observed in 1983). Finally, at the beginning. 70s was discovered notice. property of non-Abelian QFTs - asymptotic freedom It turned out that, unlike all renormalizable QFTs studied so far, for the Yang-Mills field, both pure and interacting with restrictions. number of fermions, ch. logarithmic contributions to the invariant charge have a total sign opposite to the sign of such contributions to QED:

Therefore, in the limit | k 2 |"": invariant charge and no difficulties arise when passing to the UV limit. This phenomenon of self-switching off of interaction at small distances (asymptotic freedom) made it possible to naturally explain in the gauge theory of strong interaction - quantum chromodynamics(QCD) parton structure of hadrons (see. The Partons), which had manifested itself by that time in experiments on deeply inelastic scattering of electrons on nucleons (see. Deeply inelastic processes). The symmetric basis of QCD is the group S.U.(3) c, acting in space so-called. color variables. Non-zero color quantum numbers are attributed to quarks And gluons. The specificity of color states is their unobservability at asymptotically large spatial distances. At the same time, baryons and mesons that clearly appear experimentally are singlets of the color group, i.e., their state vectors do not change during transformations in color space. When reversing the sign b [cf. (17) with (16)] the difficulty of the ghost pole passes from high energies to small ones. It is not yet known what QCD gives for ordinary energies (on the order of hadron masses), there is a hypothesis that with increasing distance (i.e., with decreasing energy), the interaction between colored particles grows so strongly that it is precisely this that does not allow quarks and gluons to disperse at a distance of /10 - 13 cm (hypothesis of non-flight, or confinement; see Color retention Very much attention is paid to the study of this problem. Thus, the study of quantum field models containing Yang-Mills fields has revealed that renormalizable theories can have an unexpected richness of content. In particular, the naive belief that the spectrum of an interacting system is qualitatively similar to the spectrum of a free system and differs from it only in a shift of levels and, possibly, the appearance of a small number of bound states, has occurred. It turned out that the spectrum of a system with interaction (hadrons) may have nothing in common with the spectrum of free particles (quarks and gluons) and therefore may not even give any indication of this. fields of which varieties should be included in the elementary microscope. Lagrangian. Establishing these essential qualities. features and holding the vast majority of quantities. QCD calculations are based on a combination of perturbation theory calculations with the requirement of renormalization group invariance. In other words, the renormalization group method has become, along with renormalized perturbation theory, one of the main modern computational tools. KTP. Dr. QFT method, received means. development since the 70s, especially in the theory of non-Abelian gauge fields, is, as already noted, a method that uses the functional integral method and is a generalization to QFT quantum mechanics. path integral method. In QFT such integrals can be considered as averaging formulas for the corresponding classical ones. expressions (for example, the classical Green's function for a particle moving in a given external field) based on quantum fluctuations of fields. Initially, the idea of ​​transferring the functional integral method to QFT was associated with the hope of obtaining compact closed expressions for the fundamentals. quantum field quantities suitable for constructive calculations. However, it turned out that due to difficulties, the math. nature, a strict definition can be given only to integrals of Gaussian type, which alone can be accurately calculated. Therefore, the functional integral representation has long been considered as a compact formal representation of quantum field perturbation theory. Later (distracting from the mathematical problem of justification) they began to use this representation in various. general tasks. Thus, the representation of the functional integral played an important role in the work on the quantization of Yang-Mills fields and the proof of their renormalizability. Interesting results were obtained using the procedure for calculating the functional integral of the functional pass method, similar to the saddle point method in the theory of functions of a complex variable. For a number of fairly simple models, using this method it was found that quantum field quantities considered as coupling constant functions g, have near the point g=0 feature of characteristic type exp(- 1 /g) and that (in full accordance with this) the coefficients fn power expansions S f n g n perturbation theories grow at large P factorial: fn~n!. Thus, what was said back in the beginning was constructively confirmed. 50s hypothesis about the non-analyticity of the charge theory. Analytics play an important role in this method. solutions to nonlinear classical levels having a localized nature ( solitons and - in the Euclidean version - instantons) and actions that provide a minimum of functionality. In the 2nd half. 70s within the framework of the method of functional integration, a direction of research arose on non-Abelian gauge fields using the so-called. contour, in k-poii as arguments instead of four-dimensional points X closed contours Г in space-time are considered. In this way, it is possible to reduce the dimension of the set of independent variables by one and, in a number of cases, significantly simplify the formulation of the quantum field problem (see. Contour approach). Successful studies were carried out using numerical calculations on a computer of functional integrals, approximately represented in the form of repeated integrals of high multiplicity. For such a representation, a discrete lattice is introduced in the original space of configuration or momentum variables. Similar, as they are called, "lattice calculations" for realism. models require the use of particularly high-power computers, as a result of which they are just beginning to become available. Here, in particular, an encouraging calculation of masses and anomalous magnetic fields was carried out using the Monte Carlo method. moments of hadrons based on quantum chromodynamics. representations (see Lattice method).
8. The big picture The development of new ideas about the world of particles and their interactions increasingly reveals two main principles. trends. This is, firstly, a gradual transition to increasingly mediated concepts and less and less visual images: local gauge symmetry, the imperative of renormalizability, the idea of ​​broken symmetries, as well as spontaneous symmetry breaking, and gluons instead of actually observed hadrons, the unobservable quantum number color and etc. Secondly, along with the complication of the arsenal of techniques and concepts used, there is an undoubted manifestation of features of the unity of principles underlying phenomena that seem to be very distant from each other, and as a consequence of this, it means. simplifying the overall picture. Three main interactions studied using QFT methods received a parallel formulation based on the principle of local gauge invariance. The related property of renormalizability gives the possibility of quantities. calculating the effects of el-magnetic, weak and strong interactions using the perturbation theory method. (Since gravitational interaction can also be formulated on the basis of this principle, it is probably universal.) From a practical point of view. perturbation theory calculation points of view have long been established in QED (e.g., the degree of agreement between theory and experiment for anomalous magnetic moment electron Dm is Dm/m 0 ~10 - 10, where m 0 is the Bohr magneton). In the theory of electroweak interaction, such calculations also turned out to have remarkable predictions. force (e.g. the masses were correctly predicted W 6 - and Z 0 -bosons). Finally, in QCD in the region of sufficiently high energies and transfers of 4-momentum Q (|Q| 2 / 100 GeV 2) based on renormalizable perturbation theory, enhanced by the renormalization method. group, it is possible to quantitatively describe a wide range of hadron physics phenomena. Due to the insufficiently small decomposition parameter: the accuracy of the calculations here is not very high. In general, we can say that, contrary to the pessimism of con. 50s, the method of renormalized perturbation theory turned out to be fruitful for at least three of the four foundations. interactions. At the same time, it should be noted that max. significant progress, achieved mainly in the 60-80s, relates specifically to understanding the mechanism of interaction of fields (and particles). Successes in observing the properties of particles and resonance states provided abundant material, which led to the discovery of new quantum numbers (strangeness, charm, etc.) and to the construction of so-called numbers corresponding to them. broken symmetries and corresponding particle taxonomies. This, in turn, gave impetus to the search for the substructure of multiples. hadrons and ultimately - the creation of QCD. As a result, such “50s” as nucleons and pions ceased to be elementary and it became possible to determine their properties (mass values, anomalous magnetic moments, etc.) through the properties of quarks and parameters of the quark-gluon interaction. This is illustrated, for example, by the degree of isotopic disturbance. symmetry, manifested in the mass difference D M charge and neutral mesons and baryons in one isotopic. multiplet (for example, p and n; Instead of the original, from the modern point of view, naive, idea that this difference (due to the numerical relation D M/M~ a) has an el-magn. origin, the belief has come that it is due to the difference in mass And- And d-quarks. However, even if the numbers are successful. In the implementation of this idea, the issue is not completely resolved - it is only moved deeper from the level of hadrons to the level of quarks. The formulation of the old riddle of the muon is transformed in a similar way: “Why is a muon needed and why, being similar to an electron, is it two hundred times heavier?” This question, transferred to the quark-lepton level, has acquired greater generality and no longer applies to a pair, but to three generations of fermions, however, did not change its essence. 9. Prospects and problems Great hopes were placed on the so-called program. grand unification interactions - combining the strong QCD interaction with the electroweak interaction at energies of the order of 10 15 GeV and higher. The starting point here is the (theoretical) observation of the fact that extrapolation to the ultrahigh energy region of formula (17) is asymptotic. freedom for chromodynamic coupling constants and formulas of type (16) for the invariant charge of QED leads to the fact that these quantities at energies of the order of |Q| = M X~10 15 b 1 GeV are compared with each other. The corresponding values ​​(as well as the value of the second charge of the theory of electroweak interaction) turn out to be equal Fundam. physical the hypothesis is that this coincidence is not accidental: in the energy region, large M X, there is some higher symmetry described by the group G, edges at lower energies are split to the observed symmetries due to mass terms, and the masses breaking the symmetries are of the order of M X. Regarding the structure of the unifying group G and the nature of the symmetry-breaking terms can be made different. assumptions [max. the simple answer is the answer G=SU(5 )], however, with quality. point of view An important feature of the association is that the fund. view (view - column) group G combines quarks and leptons from the fundam. group representations S.U.(3 )c And S.U.(2), as a result of which at energies higher M X quarks and leptons become “equal in rights”. The mechanism of local gauge interaction between them contains vector fields in the adjoint representation (representation - matrix) of the group G, quanta of which, along with gluons and heavy intermediate bosons of the electroweak interaction, contain new vector particles that connect leptons and quarks. The possibility of transformation of quarks into leptons leads to non-conservation of the baryon number. In particular, proton decay turns out to be allowed, for example, according to the scheme p""e + +p 0. It should be noted that the grand unification program encountered a number of difficulties. One of them is purely theoretical. character (the so-called hierarchy problem - the impossibility of maintaining perturbation theories of incommensurate energy scales in higher orders M X~10 15 GeV and M W~10 2 GeV). Dr. The difficulty is associated with the discrepancy between the experiments. data on proton decay from theoretical. predictions. A very promising direction of modern development. QTP is associated with supersymmetry, i.e. with symmetry with respect to transformations that “confuse” bosonic fields j ( X) (integer spin) with fermionic fields y( x) (half-integer spin). These transformations form a group that is an extension of the Poincaré group. The corresponding algebra of generators of the group, along with the usual generators of the Poincaré group, contains spinor generators, as well as anticommutators of these generators. Supersymmetry can be viewed as a non-trivial union of the Poincaré group with intrinsic. symmetries, a unification made possible by the inclusion of anticommuting generators in the algebra. Representations of the supersymmetry group - superfield Ф - are given on superspaces, including in addition to the usual coordinates X special algebraic objects (so-called forming Grassmann algebra with involution) are exactly anticommuting elements that are spinors with respect to the Poincaré group. Due to exact anticommutativity, all powers of their components, starting from the second, vanish (the corresponding Grassmann algebra is called nilpotent), and therefore the series expansions of superfields turn into polynomials. For example, in the simplest case of a chiral (or analytic) superfield, depending on the definition. basis only from q,

(s is the Pauli matrix) will be:

Odds A(X), y a ( X), F(x ) are already ordinary quantum fields - scalar, spinor, etc. They are called. component or constituent fields. From the point of view of component fields, a superfield is simply composed by definition. rules a set of a finite number of different Bose and Fermi fields with the usual quantization rules. When constructing supersymmetric models, it is required that the interactions also be invariant under supersymmetry transformations, that is, they represent superinvariant products of superfields as a whole. From an ordinary point of view, this means the introduction of a whole series of interactions of component fields, interactions whose constants are not arbitrary, but are rigidly related to each other. This opens up hope for precise compensation of all, or at least some, UV divergences originating from different interaction terms. We emphasize that an attempt to implement such compensation simply for a set of fields and interactions not limited by group requirements would be futile due to the fact that once the established compensation would be destroyed during renormalizations. Particularly interesting are supersymmetric models containing non-Abelian gauge vector fields as components. Such models, which have both gauge symmetry and supersymmetry, are called. super-calibrated. In supercalibration models, a noticeable difference is observed. fact of reduction of UV divergences. Models have been discovered in which the Lagrangian of interaction, being expressed in terms of component fields, is represented by a sum of expressions, each of which individually is renormalizable and generates a perturbation theory with a logarithm. divergences, but the divergences corresponding to the sum of the Feynman diagrams with the contributions of decomp. members of the virtual superfield compensate each other. This property of a complete reduction in divergence can be put in parallel with the well-known fact of a decrease in the degree of UV divergence of the proper. electron mass in QED in the transition from the original non-covariant calculations of the late 20s. to a virtually covariant perturbation theory that takes into account positrons in intermediate states. The analogy is strengthened by the possibility of using Feynman's supersymmetric rules, when such divergences do not appear at all. The complete reduction of UV divergences in arbitrary orders of perturbation theory, established for a number of supergauge models, gave rise to hope for theoretical Possibility of superfund pool. interactions, i.e., one constructed taking into account supersymmetry, the unification of all four interactions, including gravitational, in which not only the non-renormalizable effects of “ordinary” quantum gravity will disappear, but also the completely unified interaction will be free from UV divergences. Phys. the arena of superunifications are scales on the order of the Planck scale (energy ~10 19 GeV, distances on the order of the Planck length R Pl ~10 - 33 cm). To implement this idea, supergauge models are considered, based on superfields arranged in such a way that max. the spin of their constituent ordinary fields is equal to two. The corresponding field is identified with the gravitational one. Similar models are called supergravity (see Supergravity).Modern attempts to construct finite supergravities use ideas about Minkowski spaces with a number of dimensions greater than four, as well as about strings and superstrings. In other words, the “usual” local QFT at distances smaller than the Planck distance turns into a quantum theory of one-dimensional extended objects embedded in spaces of a higher number of dimensions. In the event that such a superunification based on supergravity. model, for which the absence of UV divergences will be proven, happens, then a unified theory of all four foundations will be constructed. interactions, free from infinities. Thus, it turns out that UV divergences will not arise at all and the entire apparatus of eliminating divergences by the renormalization method will turn out to be unnecessary. As for the nature of the particles themselves, it is possible that the theory is approaching new qualities. a milestone associated with the emergence of ideas about a level of elementaryity higher than the quark-lepton level. We are talking about the grouping of quarks and leptons into generations of fermions and the first attempts to raise the question of different scales of masses of different generations based on the prediction of the existence of particles more elementary than quarks and leptons. Lit.: Akhiezer A.I., Berestetsky V.B., Quantum electrodynamics, 4th ed., M., 1981; Bogolyubov N.N., III and r to about in D.V., Introduction to the theory of quantized fields, 4th ed., M., 1984; them, Quantum Fields, M., 1980; Berestetsky V.B., Lifshits E.M., Pitaevsky L.P., Quantum electrodynamics, 2nd ed., M., 1980; Weiskopf V.F., How we grew up with field theory, trans. from English, "UFN", 1982, vol. 138, p. 455; I ts i kson K., 3 yu b e r J--B., Quantum field theory, trans. from English, vol. 1-2, M., 1984; Bogolyubov N. N., Logunov A. A., Oksak A. I., Todorov I. T., General principles of quantum field theory, M., 1987. B. V. Medvedev, D. V. Shirkov.

Physics gives us an objective understanding of the world around us, and its laws are absolute and apply to all people without exception, regardless of social status and persons.

But such an understanding of this science was not always present. At the end of the 19th century, the first untenable steps were taken towards creating a theory of black physical body radiation based on the laws of classical physics. From the laws of this theory it followed that a substance must emit certain electromagnetic waves at any temperature, reduce the amplitude to absolute zero and lose its properties. In other words, thermal equilibrium between radiation and a specific element was impossible. However, such a statement was in conflict with real everyday experience.

Quantum physics can be explained in more detail and understandably as follows. There is a definition of an absolutely black body, which is capable of absorbing electromagnetic radiation of any wave spectrum. The length of its radiation is determined only by its temperature. In nature there cannot be absolutely black bodies that correspond to an opaque closed substance with a hole. When heated, any piece of an element begins to glow, and with a further increase in the degree it turns red, and then white. Color practically does not depend on the properties of the substance; for an absolutely black body it is characterized solely by its temperature.

Note 1

The next stage in the development of the quantum concept was the teaching of A. Einstein, which is known under the Planck hypothesis.

This theory enabled the scientist to explain all the laws of the unique photoelectric effect that do not fit within the limits of classical physics. The essence of this process is the disappearance of matter under the influence of fast electrons of electromagnetic radiation. The energy of the emitted elements does not depend on the coefficient of absorbed radiation and is determined by its characteristics. However, the number of emitted electrons depends on the saturation of the rays

Repeated experiments soon confirmed Einstein's teachings, not only with the photoelectric effect and light, but also with x-rays and gamma rays. The A. Compton effect, which was discovered in 1923, presented to the public new facts about the existence of certain photons through the arrangement of elastic scattering of electromagnetic radiation on free, small electrons, accompanied by an increase in the range and wavelength.

Quantum field theory

This doctrine allows us to determine the process of introducing quantum systems into a framework called degrees of freedom in science, which assume a certain number of independent coordinates, which are extremely important for indicating the overall movement of a mechanical concept.

In simple words, these indicators are the main characteristics of movement. It is worth noting that interesting discoveries in the field of harmonious interaction of elementary particles were made by researcher Steven Weinberg, who discovered the neutral current, namely the principle of the relationship between leptons and quarks. For his discovery in 1979, the physicist became a Nobel Prize laureate.

In quantum theory, an atom consists of a nucleus and a specific cloud of electrons. The basis of this element includes almost the entire mass of the atom itself - more than 95 percent. The nucleus has an exclusively positive charge, defining the chemical element of which the atom itself is a part. The most unusual thing about the structure of the atom is that, although the nucleus makes up almost all of its mass, it contains only one ten-thousandth of its volume. It follows from this that there is indeed very little dense matter in an atom, and the rest of the space is occupied by an electron cloud.

Interpretations of quantum theory - the principle of complementarity

The rapid development of quantum theory has led to a radical change in classical ideas about such elements:

• structure of matter;
• movement of elementary particles;
• causality;
• space;
• time;
• the nature of cognition.

Such changes in people's consciousness contributed to a radical transformation of the picture of the world into a clearer concept. The classical interpretation of a material particle was characterized by a sudden release from the environment, the presence of its own movement and a specific location in space.

In quantum theory, an elementary particle began to be represented as the most important part of the system in which it was included, but at the same time it did not have its own coordinates and momentum. In the classical cognition of movement, the transfer of elements that remained identical to themselves along a pre-planned trajectory was proposed.

The ambiguous nature of particle division necessitated the abandonment of such a vision of motion. Classical determinism gave way to the leading position to the statistical direction. If previously the entire whole in an element was perceived as the total number of component parts, then quantum theory determined the dependence of the individual properties of the atom on the system.

The classical understanding of the intellectual process was directly related to the understanding of a material object as fully existing in itself.

Quantum theory has demonstrated:

• dependence of knowledge about the object;
• independence of research procedures;
• completeness of actions on a number of hypotheses.

Note 2

The meaning of these concepts was initially far from clear, and therefore the main provisions of quantum theory have always received different interpretations, as well as various interpretations.

Quantum statistics

In parallel with the development of quantum and wave mechanics, other components of quantum theory were rapidly developing - statistics and statistical physics of quantum systems, which included a huge number of particles. On the basis of classical methods of movement of specific elements, a theory of the behavior of their integrity was created - classical statistics.

In quantum statistics there is absolutely no possibility of distinguishing between two particles of the same nature, since the two states of this unstable concept differ from each other only by the rearrangement of particles of identical power of influence on the very principle of identity. This is how quantum systems mainly differ from classical scientific systems.

An important result in the discovery of quantum statistics is the proposition that each particle that is part of any system is not identical to the same element. This implies the importance of the task of determining the specifics of a material object in a specific segment of systems.

The difference between quantum physics and classical

So, the gradual departure of quantum physics from classical physics consists in the refusal to explain individual events occurring in time and space, and the use of the statistical method with its probability waves.

Note 3

The goal of classical physics is to describe individual objects in a certain sphere and formulate laws governing the change of these objects over time.

Quantum physics occupies a special place in science in the global understanding of physical ideas. Among the most memorable creations of the human mind is the theory of relativity - general and special, which is a completely new concept of directions that combines electrodynamics, mechanics and the theory of gravity.

Quantum theory was able to finally break ties with classical traditions, creating a new, universal language and an unusual style of thinking, allowing scientists to penetrate the microworld with its energetic components and give its complete description by introducing specifics that were absent in classical physics. All these methods ultimately made it possible to understand in more detail the essence of all atomic processes, and at the same time, it was this theory that introduced an element of randomness and unpredictability into science.