Regular quadrangular truncated prism. Prism
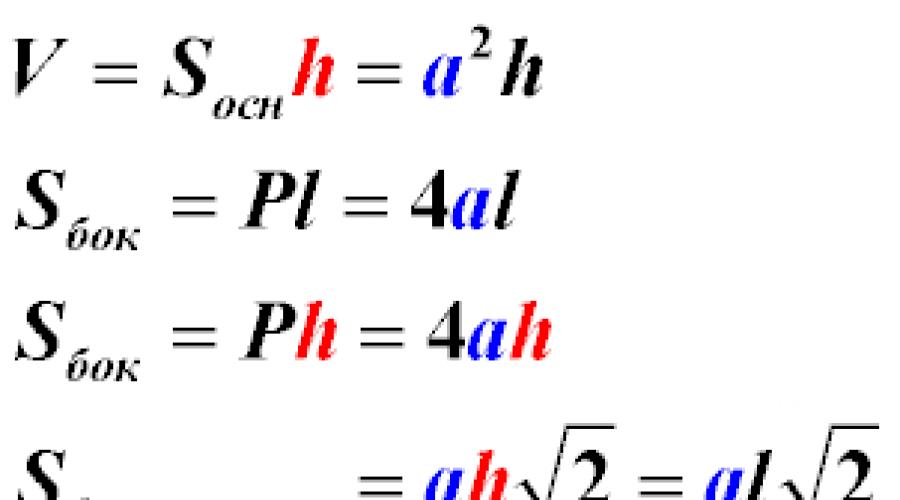
Read also
Definition.
This is a hexagon, the bases of which are two equal squares, and the side faces are equal rectangles
Side rib- is the common side of two adjacent side faces
Prism height- this is a segment perpendicular to the bases of the prism
Prism diagonal- a segment connecting two vertices of the bases that do not belong to the same face
Diagonal plane- a plane that passes through the diagonal of the prism and its lateral edges
Diagonal section- the boundaries of the intersection of the prism and the diagonal plane. The diagonal cross section of a regular quadrangular prism is a rectangle
Perpendicular section (orthogonal section)- this is the intersection of a prism and a plane drawn perpendicular to its lateral edges
Elements of a regular quadrangular prism
The figure shows two regular quadrangular prisms, which are indicated by the corresponding letters:
- The bases ABCD and A 1 B 1 C 1 D 1 are equal and parallel to each other
- Side faces AA 1 D 1 D, AA 1 B 1 B, BB 1 C 1 C and CC 1 D 1 D, each of which is a rectangle
- Lateral surface - the sum of the areas of all lateral faces of the prism
- Total surface - the sum of the areas of all bases and side faces (sum of the area of the side surface and bases)
- Side ribs AA 1, BB 1, CC 1 and DD 1.
- Diagonal B 1 D
- Base diagonal BD
- Diagonal section BB 1 D 1 D
- Perpendicular section A 2 B 2 C 2 D 2.
Properties of a regular quadrangular prism
- The bases are two equal squares
- The bases are parallel to each other
- The side faces are rectangles
- The side edges are equal to each other
- The side faces are perpendicular to the bases
- The lateral ribs are parallel to each other and equal
- Perpendicular section perpendicular to all side ribs and parallel to the bases
- Angles of perpendicular section - straight
- The diagonal cross section of a regular quadrangular prism is a rectangle
- Perpendicular (orthogonal section) parallel to the bases
Formulas for a regular quadrangular prism

Instructions for solving problems
When solving problems on the topic " regular quadrangular prism" means that:Correct prism- a prism at the base of which lies regular polygon, and the side ribs are perpendicular to the planes of the base. That is, a regular quadrangular prism contains at its base square. (see properties of a regular quadrangular prism above) Note. This is part of a lesson with geometry problems (section stereometry - prism). Here are problems that are difficult to solve. If you need to solve a geometry problem that is not here, write about it in the forum. To indicate the action of retrieving square root the symbol is used in solving problems√ .
Task.
In a regular quadrangular prism, the base area is 144 cm 2 and the height is 14 cm. Find the diagonal of the prism and the area full surface.Solution.
A regular quadrilateral is a square.
Accordingly, the side of the base will be equal
From where the diagonal of the base of a regular rectangular prism will be equal to
√(12 2 + 12 2 ) = √288 = 12√2
The diagonal of a regular prism forms with the diagonal of the base and the height of the prism right triangle. Accordingly, according to the Pythagorean theorem, the diagonal of a given regular quadrangular prism will be equal to:
√((12√2) 2 + 14 2 ) = 22 cm
Answer: 22 cm
Task
Determine the total surface of a regular quadrangular prism if its diagonal is 5 cm and the diagonal of its side face is 4 cm.Solution.
Since the base of a regular quadrangular prism is a square, we find the side of the base (denoted as a) using the Pythagorean theorem:
A 2 + a 2 = 5 2
2a 2 = 25
a = √12.5
The height of the side face (denoted as h) will then be equal to:
H 2 + 12.5 = 4 2
h 2 + 12.5 = 16
h 2 = 3.5
h = √3.5
The total surface area will be equal to the sum of the lateral surface area and twice the base area
S = 2a 2 + 4ah
S = 25 + 4√12.5 * √3.5
S = 25 + 4√43.75
S = 25 + 4√(175/4)
S = 25 + 4√(7*25/4)
S = 25 + 10√7 ≈ 51.46 cm 2.
Answer: 25 + 10√7 ≈ 51.46 cm 2.
Polyhedra
The main object of study of stereometry is spatial bodies. Body represents a part of space limited by a certain surface.
Polyhedron is a body whose surface consists of a finite number of flat polygons. A polyhedron is called convex if it is located on one side of the plane of every plane polygon on its surface. The common part of such a plane and the surface of a polyhedron is called edge. The faces of a convex polyhedron are flat convex polygons. The sides of the faces are called edges of the polyhedron, and the vertices are vertices of the polyhedron.
For example, a cube consists of six squares, which are its faces. It contains 12 edges (the sides of the squares) and 8 vertices (the tops of the squares).
The simplest polyhedra are prisms and pyramids, which we will study further.
Prism
Definition and properties of a prism
Prism is a polyhedron consisting of two flat polygons lying in parallel planes combined by parallel translation, and all segments connecting the corresponding points of these polygons. Polygons are called prism bases, and the segments connecting the corresponding vertices of the polygons are lateral edges of the prism.

Prism height is called the distance between the planes of its bases (). A segment connecting two vertices of a prism that do not belong to the same face is called prism diagonal(). The prism is called n-carbon, if its base contains an n-gon.
Any prism has the following properties, resulting from the fact that the bases of the prism are combined by parallel translation:
1. The bases of the prism are equal.
2. The lateral edges of the prism are parallel and equal.
The surface of the prism consists of bases and lateral surface. The lateral surface of the prism consists of parallelograms (this follows from the properties of the prism). The area of the lateral surface of a prism is the sum of the areas of the lateral faces.
Straight prism
The prism is called straight, if its lateral edges are perpendicular to the bases. Otherwise the prism is called inclined.
The faces of a right prism are rectangles. The height of a straight prism is equal to its side faces.
Full prism surface is called the sum of the lateral surface area and the areas of the bases.
With the right prism called a right prism with a regular polygon at its base.
Theorem 13.1. The area of the lateral surface of a straight prism is equal to the product of the perimeter and the height of the prism (or, which is the same, by the lateral edge).
Proof. The lateral faces of a right prism are rectangles, the bases of which are the sides of the polygons at the bases of the prism, and the heights are the lateral edges of the prism. Then, by definition, the lateral surface area is:
![]() ,
,
where is the perimeter of the base of a straight prism.
Parallelepiped
If parallelograms lie at the bases of a prism, then it is called parallelepiped. All faces of a parallelepiped are parallelograms. In this case, the opposite faces of the parallelepiped are parallel and equal.
Theorem 13.2. The diagonals of a parallelepiped intersect at one point and are divided in half by the intersection point.

Proof. Consider two arbitrary diagonals, for example, and . Because the faces of a parallelepiped are parallelograms, then and , which means according to To there are two straight lines parallel to the third. In addition, this means that straight lines and lie in the same plane (plane). This plane intersects parallel planes and along parallel lines and . Thus, a quadrilateral is a parallelogram, and by the property of a parallelogram, its diagonals intersect and are divided in half by the intersection point, which was what needed to be proven.
A right parallelepiped whose base is a rectangle is called rectangular parallelepiped. All faces of a rectangular parallelepiped are rectangles. The lengths of non-parallel edges of a rectangular parallelepiped are called its linear dimensions(measurements). There are three such sizes (width, height, length).
Theorem 13.3. In a rectangular parallelepiped, the square of any diagonal is equal to the sum of the squares of its three dimensions ![]() (proved by applying Pythagorean T twice).
(proved by applying Pythagorean T twice).
Rectangular parallelepiped, which has all edges equal, is called cube.
Tasks
13.1 How many diagonals does it have? n-carbon prism
13.2 In an inclined triangular prism, the distances between the side edges are 37, 13 and 40. Find the distance between the larger side edge and the opposite side edge.
13.3 A plane is drawn through the side of the lower base of a regular triangular prism, intersecting the side faces along segments with an angle between them. Find the angle of inclination of this plane to the base of the prism.
General information about straight prism
The lateral surface of a prism (more precisely, the lateral surface area) is called sum areas of the side faces. The total surface of the prism is equal to the sum of the lateral surface and the areas of the bases.
Theorem 19.1. The lateral surface of a straight prism is equal to the product of the perimeter of the base and the height of the prism, i.e., the length of the side edge.
Proof. The lateral faces of a straight prism are rectangles. The bases of these rectangles are the sides of the polygon lying at the base of the prism, and the heights are equal to the length of the side edges. It follows that side surface prism is equal
S = a 1 l + a 2 l + ... + a n l = pl,
where a 1 and n are the lengths of the base edges, p is the perimeter of the base of the prism, and I is the length of the side edges. The theorem has been proven.
Practical task
Problem (22) . In an inclined prism it is carried out section, perpendicular to the side ribs and intersecting all the side ribs. Find the lateral surface of the prism if the cross-sectional perimeter is equal to p and the side edges are equal to l.
Solution. The plane of the drawn section divides the prism into two parts (Fig. 411). Let us subject one of them to parallel translation, combining the bases of the prism. In this case, we obtain a straight prism, the base of which is the cross-section of the original prism, and the side edges are equal to l. This prism has the same lateral surface as the original one. Thus, the lateral surface of the original prism is equal to pl.
Summary of the covered topic
Now let’s try to summarize the topic we covered about prisms and remember what properties a prism has.

Prism properties
Firstly, a prism has all its bases as equal polygons;
Secondly, in a prism all its lateral faces are parallelograms;
Thirdly, in such a multifaceted figure as a prism, all lateral edges are equal;
Also, it should be remembered that polyhedra such as prisms can be straight or inclined.
Which prism is called a straight prism?
If the side edge of a prism is located perpendicular to the plane of its base, then such a prism is called a straight one.
It would not be superfluous to recall that the lateral faces of a straight prism are rectangles.
What type of prism is called oblique?
But if the side edge of a prism is not located perpendicular to the plane of its base, then we can safely say that it is an inclined prism.
Which prism is called correct?

If a regular polygon lies at the base of a straight prism, then such a prism is regular.
Now let us remember the properties that a regular prism has.
Properties of a regular prism
Firstly, regular polygons always serve as the bases of a regular prism;
Secondly, if we consider the side faces of a regular prism, they are always equal rectangles;
Thirdly, if you compare the sizes of the side ribs, then in a regular prism they are always equal.
Fourthly, a correct prism is always straight;
Fifthly, if in a regular prism the side faces have the shape of squares, then such a figure is usually called a semi-regular polygon.
Prism cross section
Now let's look at the cross section of the prism:

Homework
Now let's try to consolidate the topic we've learned by solving problems.
Let's draw an inclined triangular prism, the distance between its edges will be equal to: 3 cm, 4 cm and 5 cm, and the lateral surface of this prism will be equal to 60 cm2. Having these parameters, find the side edge of this prism.
Do you know that geometric figures constantly surround us not only in geometry lessons, but also in Everyday life There are objects that resemble one or another geometric figure.

Everyone at home, at school or at work has a computer, system unit which has the shape of a straight prism.
If you pick up a simple pencil, you will see that the main part of the pencil is a prism.
Walking along the central street of the city, we see that under our feet lies a tile that has the shape of a hexagonal prism.
A. V. Pogorelov, Geometry for grades 7-11, Textbook for educational institutions
How does she look
Rectangular prisms surrounded modern man quite a bit of. This is, for example, ordinary cardboard for shoes, computer components, etc. Look around. Even in a room you will probably see many rectangular prisms. This and computer case, and a bookcase, and a refrigerator, and a closet, and many other items. The shape is extremely popular mainly because it allows you to make the most of your space, whether you're decorating your interior or packing things into cardboard before moving.Properties of a rectangular prism
A rectangular prism has a number of specific properties. Any pair of faces can serve as it, since all adjacent faces are located at the same angle to each other, and this angle is 90°. The volume and surface area of a rectangular prism are easier to calculate than any other. Take any object that has the shape of a rectangular prism. Measure its length, width and height. To find the volume, just multiply these measurements. That is, the formula looks like this: V=a*b*h, where V is the volume, a and b are the sides of the base, h is the height that coincides with the side edge of this geometric body. The base area is calculated using the formula S1=a*b. For the side surface, you must first calculate the perimeter of the base using the formula P=2(a+b), and then multiply it by the height. The resulting formula is S2=P*h=2(a+b)*h. To calculate the total surface area of a rectangular prism, add twice the base area and the side surface area. The formula is S=2S1+S2=2*a*b+2*(a+b)*h=2IN school curriculum In a stereometry course, the study of three-dimensional figures usually begins with a simple geometric body - the polyhedron of a prism. The role of its bases is performed by 2 equal polygons lying in parallel planes. A special case is a regular quadrangular prism. Its bases are 2 identical regular quadrangles, to which the sides are perpendicular, having the shape of parallelograms (or rectangles, if the prism is not inclined).
What does a prism look like?
A regular quadrangular prism is a hexagon, the bases of which are 2 squares, and the side faces are represented by rectangles. Another name for this geometric figure- straight parallelepiped.
A drawing showing a quadrangular prism is shown below.
You can also see in the picture essential elements, of which the geometric body consists. These include:
Sometimes in geometry problems you can come across the concept of a section. The definition will sound like this: a section is all the points of a volumetric body belonging to a cutting plane. The section can be perpendicular (intersects the edges of the figure at an angle of 90 degrees). For a rectangular prism, a diagonal section is also considered ( maximum amount sections that can be constructed - 2), passing through 2 edges and diagonals of the base.

If the section is drawn in such a way that the cutting plane is not parallel to either the bases or the side faces, the result is a truncated prism.
To find the reduced prismatic elements, various relations and formulas are used. Some of them are known from the planimetry course (for example, to find the area of the base of a prism, it is enough to recall the formula for the area of a square).
Surface area and volume
To determine the volume of a prism using the formula, you need to know the area of its base and height:
V = Sbas h
Since the base of a regular tetrahedral prism is a square with side a, You can write the formula in more detailed form:
V = a²·h
If we are talking about a cube - a regular prism with equal length, width and height, the volume is calculated as follows:
To understand how to find the lateral surface area of a prism, you need to imagine its development.

From the drawing it can be seen that the side surface is made up of 4 equal rectangles. Its area is calculated as the product of the perimeter of the base and the height of the figure:
Sside = Posn h
Taking into account that the perimeter of the square is equal to P = 4a, the formula takes the form:
Sside = 4a h
For cube:
Sside = 4a²
To calculate the total surface area of the prism, you need to add 2 base areas to the lateral area:
Sfull = Sside + 2Smain
In relation to a quadrangular regular prism, the formula looks like:
Stotal = 4a h + 2a²
For the surface area of a cube:
Sfull = 6a²
Knowing the volume or surface area, you can calculate individual elements geometric body.
Finding prism elements
Often there are problems in which the volume is given or the value of the lateral surface area is known, where it is necessary to determine the length of the side of the base or the height. In such cases, the formulas can be derived:
- base side length: a = Sside / 4h = √(V / h);
- height or side rib length: h = Sside / 4a = V / a²;
- base area: Sbas = V / h;
- side face area: Side gr = Sside / 4.
 To determine how much area the diagonal section has, you need to know the length of the diagonal and the height of the figure. For a square d = a√2. Therefore:
To determine how much area the diagonal section has, you need to know the length of the diagonal and the height of the figure. For a square d = a√2. Therefore:
Sdiag = ah√2
To calculate the diagonal of a prism, use the formula:
dprize = √(2a² + h²)
To understand how to apply the given relationships, you can practice and solve several simple tasks.
Examples of problems with solutions
Here are some tasks found on state final exams in mathematics.

Exercise 1.
Sand is poured into a box shaped like a regular quadrangular prism. The height of its level is 10 cm. What will the sand level be if you move it into a container of the same shape, but with a base twice as long?
It should be reasoned as follows. The amount of sand in the first and second containers did not change, i.e. its volume in them is the same. You can denote the length of the base by a. In this case, for the first box the volume of the substance will be:
V₁ = ha² = 10a²
For the second box, the length of the base is 2a, but the height of the sand level is unknown:
V₂ = h (2a)² = 4ha²
Because the V₁ = V₂, we can equate the expressions:
10a² = 4ha²
After reducing both sides of the equation by a², we get:
As a result new level sand will be h = 10 / 4 = 2.5 cm.

Task 2.
ABCDA₁B₁C₁D₁ is a correct prism. It is known that BD = AB₁ = 6√2. Find the total surface area of the body.
To make it easier to understand which elements are known, you can draw a figure.
Since we are talking about a regular prism, we can conclude that at the base there is a square with a diagonal of 6√2. The diagonal of the side face has the same size, therefore, the side face also has the shape of a square equal to the base. It turns out that all three dimensions - length, width and height - are equal. We can conclude that ABCDA₁B₁C₁D₁ is a cube.
The length of any edge is determined through a known diagonal:
a = d / √2 = 6√2 / √2 = 6
The total surface area is found using the formula for a cube:
Sfull = 6a² = 6 6² = 216

Task 3.
The room is being renovated. It is known that its floor has the shape of a square with an area of 9 m². The height of the room is 2.5 m. What is the lowest cost of wallpapering a room if 1 m² costs 50 rubles?
Since the floor and ceiling are squares, i.e. regular quadrangles, and its walls are perpendicular to horizontal surfaces, we can conclude that it is the right prism. It is necessary to determine the area of its lateral surface.
The length of the room is a = √9 = 3 m.
The area will be covered with wallpaper Sside = 4 3 2.5 = 30 m².
The lowest cost of wallpaper for this room will be 50·30 = 1500 rubles
Thus, to solve problems involving a rectangular prism, it is enough to be able to calculate the area and perimeter of a square and rectangle, as well as to know the formulas for finding the volume and surface area.
How to find the area of a cube














