Rules for reducing fractions with examples. Online calculator. Reducing fractions (irregular, mixed)
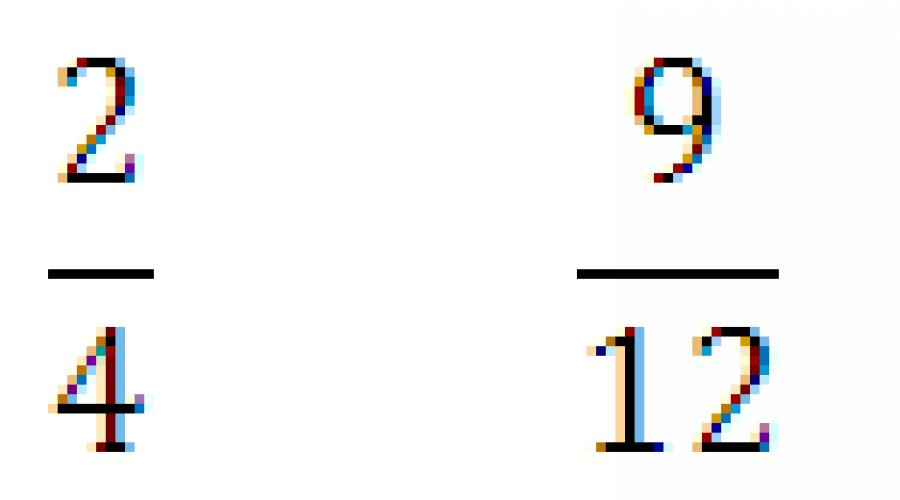
Read also
So, we already know that the numerator and denominator of a fraction can be multiplied and divided by the same number, the fraction will not change. Let's consider three approaches:
Approach one.
To reduce, divide the numerator and denominator by common divisor. Let's look at examples:

Let's shorten:
In the examples given, we immediately see which divisors to take for reduction. The process is simple - we go through 2,3,4,5 and so on. In most school course examples, this is quite enough. But if it’s a fraction:

Here the process of selecting divisors can take a long time;). Of course, such examples are outside the school curriculum, but you need to be able to cope with them. Below we will look at how this is done. For now, let's get back to the downsizing process.
As discussed above, in order to reduce a fraction, we divided by the common divisor(s) we determined. Everything is correct! One has only to add signs of divisibility of numbers:
- if the number is even, then it is divisible by 2.
- if a number from the last two digits is divisible by 4, then the number itself is divisible by 4.
— if the sum of the digits that make up the number is divisible by 3, then the number itself is divisible by 3. For example, 125031, 1+2+5+0+3+1=12. Twelve is divisible by 3, so 123031 is divisible by 3.
- if the number ends with 5 or 0, then the number is divisible by 5.
— if the sum of the digits that make up the number is divisible by 9, then the number itself is divisible by 9. For example, 625032 =.> 6+2+5+0+3+2=18. Eighteen is divisible by 9, which means 623032 is divisible by 9.
Second approach.
To put it briefly, in fact, the whole action comes down to factoring the numerator and denominator and then reducing equal factors in the numerator and denominator (this approach is a consequence of the first approach):

Visually, in order to avoid confusion and mistakes, equal factors are simply crossed out. Question - how to factor a number? It is necessary to determine all divisors by searching. This is a separate topic, it is not complicated, look up the information in a textbook or on the Internet. You won't encounter any big problems with factoring numbers that are present in school fractions.
Formally, the reduction principle can be written as follows:

Approach three.
Here is the most interesting thing for the advanced and those who want to become one. Let's reduce the fraction 143/273. Try it yourself! Well, how did it happen quickly? Now look!
We turn it over (we change places of the numerator and denominator). Divide the resulting fraction with a corner and convert it to mixed number, that is, we select the whole part:

It's already easier. We see that the numerator and denominator can be reduced by 13:


Now don’t forget to flip the fraction back again, let’s write down the whole chain:

Checked - it takes less time than searching through and checking divisors. Let's return to our two examples:

First. Divide with a corner (not on a calculator), we get:

This fraction is simpler, of course, but the reduction is again a problem. Now we separately analyze the fraction 1273/1463 and turn it over:

It's easier here. We can consider a divisor such as 19. The rest are not suitable, this is clear: 190:19 = 10, 1273:19 = 67. Hurray! Let's write down:

Next example. Let's shorten it to 88179/2717.
Divide, we get:

Separately, we analyze the fraction 1235/2717 and turn it over:

We can consider a divisor such as 13 (up to 13 is not suitable):
Numerator 247:13=19 Denominator 1235:13=95
*During the process we saw another divisor equal to 19. It turns out that:

Now we write down the original number:
And it doesn’t matter what is larger in the fraction - the numerator or the denominator, if it is the denominator, then we turn it over and act as described. This way we can reduce any fraction; the third approach can be called universal.
Of course, the two examples discussed above are not simple examples. Let's try this technology on the “simple” fractions we have already considered:

Two quarters.
Seventy-two sixties. The numerator is greater than the denominator; there is no need to reverse it:
Of course, the third approach was applied to such simple examples just as an alternative. The method, as already said, is universal, but not convenient and correct for all fractions, especially for simple ones.
The variety of fractions is great. It is important that you understand the principles. Strict rules there is simply no way to work with fractions. We looked, figured out how it would be more convenient to act, and moved forward. With practice, skill will come and you will crack them like seeds.
Conclusion:
If you see a common divisor(s) for the numerator and denominator, use them to reduce.
If you know how to quickly factor a number, then factor the numerator and denominator, then reduce.
If you can’t determine the common divisor, then use the third approach.
*To reduce fractions, it is important to master the principles of reduction, understand the basic property of a fraction, know approaches to solving, and be extremely careful when making calculations.
And remember! It is customary to reduce a fraction until it stops, that is, reduce it as long as there is a common divisor.
Sincerely, Alexander Krutitskikh.
Reducing fractions is necessary in order to reduce the fraction to more simple view, for example, in the answer obtained as a result of solving an expression.
Reducing fractions, definition and formula.
What is reducing fractions? What does it mean to reduce a fraction?
Definition:
Reducing Fractions- this is the division of a fraction's numerator and denominator by the same positive number not equal to zero and one. As a result of the reduction, a fraction with a smaller numerator and denominator is obtained, equal to the previous fraction according to.
Formula for reducing fractions main property rational numbers.
\(\frac(p \times n)(q \times n)=\frac(p)(q)\)
Let's look at an example:
Reduce the fraction \(\frac(9)(15)\)
Solution:
We can expand the fraction into prime factors and reduce common factors.
\(\frac(9)(15)=\frac(3 \times 3)(5 \times 3)=\frac(3)(5) \times \color(red) (\frac(3)(3) )=\frac(3)(5) \times 1=\frac(3)(5)\)
Answer: after reduction we got the fraction \(\frac(3)(5)\). According to the basic property of rational numbers, the original and resulting fractions are equal.
\(\frac(9)(15)=\frac(3)(5)\)
How to reduce fractions? Reducing a fraction to its irreducible form.
To get an irreducible fraction as a result, we need find the greatest common divisor (GCD) for the numerator and denominator of the fraction.
There are several ways to find GCD; in the example we will use the decomposition of numbers into prime factors.
Get the irreducible fraction \(\frac(48)(136)\).
Solution:
Let's find GCD(48, 136). Let's write the numbers 48 and 136 into prime factors.
48=2⋅2⋅2⋅2⋅3
136=2⋅2⋅2⋅17
GCD(48, 136)= 2⋅2⋅2=6
\(\frac(48)(136)=\frac(\color(red) (2 \times 2 \times 2) \times 2 \times 3)(\color(red) (2 \times 2 \times 2) \times 17)=\frac(\color(red) (6) \times 2 \times 3)(\color(red) (6) \times 17)=\frac(2 \times 3)(17)=\ frac(6)(17)\)
The rule for reducing a fraction to an irreducible form.
- You need to find the greatest common divisor for the numerator and denominator.
- You need to divide the numerator and denominator by the greatest common divisor to obtain an irreducible fraction.
Example:
Reduce the fraction \(\frac(152)(168)\).
Solution:
Let's find GCD(152, 168). Let's write the numbers 152 and 168 into prime factors.
152=2⋅2⋅2⋅19
168=2⋅2⋅2⋅3⋅7
GCD(152, 168)= 2⋅2⋅2=6
\(\frac(152)(168)=\frac(\color(red) (6) \times 19)(\color(red) (6) \times 21)=\frac(19)(21)\)
Answer: \(\frac(19)(21)\) is an irreducible fraction.
Reducing improper fractions.
How to cut improper fraction?
The rules for reducing fractions are the same for proper and improper fractions.
Let's look at an example:
Reduce the improper fraction \(\frac(44)(32)\).
Solution:
Let's write the numerator and denominator into simple factors. And then we’ll reduce the common factors.
\(\frac(44)(32)=\frac(\color(red) (2 \times 2 ) \times 11)(\color(red) (2 \times 2 ) \times 2 \times 2 \times 2 )=\frac(11)(2 \times 2 \times 2)=\frac(11)(8)\)
Reducing mixed fractions.
Mixed fractions follow the same rules as ordinary fractions. The only difference is that we can do not touch the whole part, but reduce the fractional part or mixed fraction convert to an improper fraction, reduce and convert back to a proper fraction.
Let's look at an example:
Cancel the mixed fraction \(2\frac(30)(45)\).
Solution:
Let's solve it in two ways:
First way:
Let's write the fractional part into simple factors, but we won't touch the whole part.
\(2\frac(30)(45)=2\frac(2 \times \color(red) (5 \times 3))(3 \times \color(red) (5 \times 3))=2\ frac(2)(3)\)
Second way:
Let's first convert it to an improper fraction, and then write it into prime factors and reduce. Let's convert the resulting improper fraction into a proper fraction.
\(2\frac(30)(45)=\frac(45 \times 2 + 30)(45)=\frac(120)(45)=\frac(2 \times \color(red) (5 \times 3) \times 2 \times 2)(3 \times \color(red) (3 \times 5))=\frac(2 \times 2 \times 2)(3)=\frac(8)(3)= 2\frac(2)(3)\)
Questions on the topic:
Can you reduce fractions when adding or subtracting?
Answer: no, you must first add or subtract fractions according to the rules, and only then reduce them. Let's look at an example:
Evaluate the expression \(\frac(50+20-10)(20)\) .
Solution:
They often make the mistake of abbreviating same numbers In our case, the numerator and denominator have the number 20, but they cannot be reduced until you have completed the addition and subtraction.
\(\frac(50+\color(red) (20)-10)(\color(red) (20))=\frac(60)(20)=\frac(3 \times 20)(20)= \frac(3)(1)=3\)
What numbers can you reduce a fraction by?
Answer: You can reduce a fraction by the greatest common factor or the common divisor of the numerator and denominator. For example, the fraction \(\frac(100)(150)\).
Let's write the numbers 100 and 150 into prime factors.
100=2⋅2⋅5⋅5
150=2⋅5⋅5⋅3
The greatest common divisor will be the number gcd(100, 150)= 2⋅5⋅5=50
\(\frac(100)(150)=\frac(2 \times 50)(3 \times 50)=\frac(2)(3)\)
We got the irreducible fraction \(\frac(2)(3)\).
But it is not necessary to always divide by GCD; an irreducible fraction is not always needed; you can reduce the fraction by a simple divisor of the numerator and denominator. For example, the number 100 and 150 have a common divisor of 2. Let's reduce the fraction \(\frac(100)(150)\) by 2.
\(\frac(100)(150)=\frac(2 \times 50)(2 \times 75)=\frac(50)(75)\)
We got the reducible fraction \(\frac(50)(75)\).
What fractions can be reduced?
Answer: You can reduce fractions in which the numerator and denominator have a common divisor. For example, the fraction \(\frac(4)(8)\). The number 4 and 8 have a number by which they are both divisible - the number 2. Therefore, such a fraction can be reduced by the number 2.
Example:
Compare the two fractions \(\frac(2)(3)\) and \(\frac(8)(12)\).
These two fractions are equal. Let's take a closer look at the fraction \(\frac(8)(12)\):
\(\frac(8)(12)=\frac(2 \times 4)(3 \times 4)=\frac(2)(3) \times \frac(4)(4)=\frac(2) (3) \times 1=\frac(2)(3)\)
From here we get, \(\frac(8)(12)=\frac(2)(3)\)
Two fractions are equal if and only if one of them is obtained by reducing the other fraction by the common factor of the numerator and denominator.
Example:
If possible, reduce the following fractions: a) \(\frac(90)(65)\) b) \(\frac(27)(63)\) c) \(\frac(17)(100)\) d) \(\frac(100)(250)\)
Solution:
a) \(\frac(90)(65)=\frac(2 \times \color(red) (5) \times 3 \times 3)(\color(red) (5) \times 13)=\frac (2 \times 3 \times 3)(13)=\frac(18)(13)\)
b) \(\frac(27)(63)=\frac(\color(red) (3 \times 3) \times 3)(\color(red) (3 \times 3) \times 7)=\frac (3)(7)\)
c) \(\frac(17)(100)\) irreducible fraction
d) \(\frac(100)(250)=\frac(\color(red) (2 \times 5 \times 5) \times 2)(\color(red) (2 \times 5 \times 5) \ times 5)=\frac(2)(5)\)
Let's understand what is the reduction of fractions, why and how to reduce fractions, we will give the rule for reducing fractions and examples of its use.
Yandex.RTB R-A-339285-1
What is "reducing fractions"
Reduce fractionTo reduce a fraction is to divide its numerator and denominator by a common factor that is positive and different from one.
As a result of this action, a fraction with a new numerator and denominator will be obtained, equal to the original fraction.
For example, let's take common fraction 6 24 and shorten it. Divide the numerator and denominator by 2, resulting in 6 24 = 6 ÷ 2 24 ÷ 2 = 3 12. In this example, we reduced the original fraction by 2.
Reducing fractions to irreducible form
In the previous example, we reduced the fraction 6 24 by 2, resulting in the fraction 3 12. It is easy to see that this fraction can be further reduced. Typically, the goal of reducing fractions is to end up with an irreducible fraction. How to reduce a fraction to its irreducible form?
This can be done by reducing the numerator and denominator by their greatest common factor (GCD). Then, by the property of the greatest common divisor, the numerator and denominator will have mutually prime numbers, and the fraction will be irreducible.
a b = a ÷ N O D (a , b) b ÷ N O D (a , b)
Reducing a fraction to an irreducible form
To reduce a fraction to an irreducible form, you need to divide its numerator and denominator by their gcd.
Let's return to the fraction 6 24 from the first example and bring it to its irreducible form. The greatest common divisor of the numbers 6 and 24 is 6. Let's reduce the fraction:
6 24 = 6 ÷ 6 24 ÷ 6 = 1 4
Reducing fractions is convenient to use so as not to work with large numbers. In general, there is an unspoken rule in mathematics: if you can simplify any expression, then you need to do it. Reducing a fraction most often means reducing it to an irreducible form, and not simply reducing it by the common divisor of the numerator and denominator.
Rule for reducing fractions
To reduce fractions, just remember the rule, which consists of two steps.
Rule for reducing fractions
To reduce a fraction you need:
- Find the gcd of the numerator and denominator.
- Divide the numerator and denominator by their gcd.
Let's look at practical examples.
Example 1. Let's reduce the fraction.
Given the fraction 182 195. Let's shorten it.
Let's find the gcd of the numerator and denominator. For this purpose in in this case It is most convenient to use the Euclidean algorithm.
195 = 182 1 + 13 182 = 13 14 N O D (182, 195) = 13
Divide the numerator and denominator by 13. We get:
182 195 = 182 ÷ 13 195 ÷ 13 = 14 15
Ready. We have obtained an irreducible fraction that is equal to the original fraction.
How else can you reduce fractions? In some cases, it is convenient to factor the numerator and denominator into simple factors, and then from the upper and lower parts fractions, remove all common factors.
Example 2. Reduce the fraction
Given the fraction 360 2940. Let's shorten it.
To do this, imagine the original fraction in the form:
360 2940 = 2 2 2 3 3 5 2 2 3 5 7 7
Let's get rid of the common factors in the numerator and denominator, resulting in:
360 2940 = 2 2 2 3 3 5 2 2 3 5 7 7 = 2 3 7 7 = 6 49
Finally, let's look at another way to reduce fractions. This is the so-called sequential reduction. Using this method, the reduction is carried out in several stages, in each of which the fraction is reduced by some obvious common factor.
Example 3. Reduce the fraction
Let's reduce the fraction 2000 4400.
It is immediately clear that the numerator and denominator have a common factor of 100. We reduce the fraction by 100 and get:
2000 4400 = 2000 ÷ 100 4400 ÷ 100 = 20 44
20 44 = 20 ÷ 2 44 ÷ 2 = 10 22
We reduce the resulting result again by 2 and obtain an irreducible fraction:
10 22 = 10 ÷ 2 22 ÷ 2 = 5 11
If you notice an error in the text, please highlight it and press Ctrl+Enter
Many students make the same mistakes when working with fractions. And all because they forget the basic rules arithmetic. Today we will repeat these rules on specific tasks which I give in my classes.
Here is the task that I offer to everyone who is preparing for the Unified State Exam in mathematics:
Task. Harbour porpoise eats 150 grams of food per day. But she grew up and began to eat 20% more. How many grams of feed does the pig eat now?
Not correct solution. This is a percentage problem that boils down to the equation:
Many (very many) reduce the number 100 in the numerator and denominator of a fraction:
This is the mistake my student made right on the day of writing this article. Numbers that have been truncated are marked in red.
Needless to say, the answer was wrong. Judge for yourself: the pig ate 150 grams, but began to eat 3150 grams. The increase is not 20%, but 21 times, i.e. by 2000%.
To avoid such misunderstandings, remember the basic rule:
Only multipliers can be reduced. The terms cannot be reduced!
Thus, the correct solution to the previous problem looks like this:
Numbers that are abbreviated in the numerator and denominator are marked in red. As you can see, the numerator is the product, the denominator is ordinary number. Therefore, the reduction is completely legal.
Working with proportions
Another problem area — proportions. Especially when the variable is on both sides. For example:
Task. Solve the equation:
Wrong solution - some people are literally itching to shorten everything by m:
![]()
Reduced variables are shown in red. The expression 1/4 = 1/5 turns out to be complete nonsense, these numbers are never equal.
And now - the right decision. Essentially it's ordinary linear equation . It can be solved either by moving all elements to one side, or by the basic property of proportion:
Many readers will object: “Where is the mistake in the first solution?” Well, let's figure it out. Let's remember the rule for working with equations:
Any equation can be divided and multiplied by any number, non-zero.
Did you miss the trick? You can only divide by numbers non-zero. In particular, you can divide by a variable m only if m != 0. But what if, after all, m = 0? Let's substitute and check:
![]()
We received the correct numerical equality, i.e. m = 0 is the root of the equation. For the remaining m != 0 we get an expression of the form 1/4 = 1/5, which is naturally incorrect. Thus, there are no non-zero roots.
Conclusions: putting it all together
So, to solve fractional rational equations remember three rules:
- Only multipliers can be reduced. Addends are not possible. Therefore, learn to factor the numerator and denominator;
- The main property of proportion: the product of the extreme elements is equal to the product of the middle ones;
- Equations can only be multiplied and divided by numbers k other than zero. The case k = 0 must be checked separately.
Remember these rules and don't make mistakes.
To understand how to reduce fractions, let's first look at an example.
To reduce a fraction means to divide the numerator and denominator by the same thing. Both 360 and 420 end in a number, so we can reduce this fraction by 2. B new fraction Both 180 and 210 are also divisible by 2, so we reduce this fraction by 2. In the numbers 90 and 105, the sum of the digits is divisible by 3, so both of these numbers are divisible by 3, we reduce the fraction by 3. In the new fraction, 30 and 35 end in 0 and 5, which means both numbers are divisible by 5, so we reduce the fraction by 5. The resulting fraction six-sevenths is irreducible. This is the final answer.
We can arrive at the same answer in a different way.
![]()
Both 360 and 420 end in zero, which means they are divisible by 10. We reduce the fraction by 10. In the new fraction, both the numerator 36 and the denominator 42 are divided by 2. We reduce the fraction by 2. In the next fraction, both the numerator 18 and the denominator 21 are divided by 3, which means we reduce the fraction by 3. We came to the result - six sevenths.
And one more solution.
![]()
Next time we'll look at examples of reducing fractions.