Least common denominator (LCD) of algebraic fractions, finding it. Reducing fractions to the lowest common denominator, rule, examples, solutions

27.09.2019

Reviews of the book The True, Mad, Guilty Moriarty l The True, Mad, Guilty

Life at Full Power - Jim Lauer, Tony Schwartz

Famous pirates of the Caribbean, next to whom the movie Jack Sparrow is just a boy

To solve examples with fractions, you need to be able to find the lowest common denominator. Below are detailed instructions.

How to find the lowest common denominator - concept

Least common denominator (LCD) in simple words is the minimum number that is divisible by the denominators of all fractions in this example. In other words, it is called the Least Common Multiple (LCM). NOS is used only if the denominators of the fractions are different.

How to find the lowest common denominator - examples

Let's look at examples of finding NOCs.

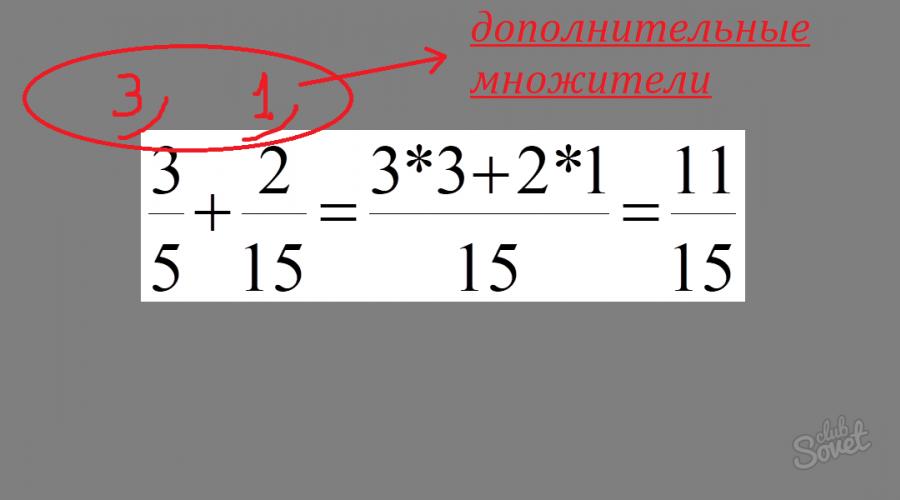
Calculate: 3/5 + 2/15.

Solution (Sequence of actions):

We look at the denominators of the fractions, make sure that they are different and that the expressions are as abbreviated as possible.
We find the smallest number that is divisible by both 5 and 15. This number will be 15. Thus, 3/5 + 2/15 = ?/15.
We figured out the denominator. What will be in the numerator? An additional multiplier will help us figure this out. An additional factor is the number obtained by dividing the NZ by the denominator of a particular fraction. For 3/5, the additional factor is 3, since 15/5 = 3. For the second fraction, the additional factor is 1, since 15/15 = 1.
Having found out the additional factor, we multiply it by the numerators of the fractions and add the resulting values. 3/5 + 2/15 = (3*3+2*1)/15 = (9+2)/15 = 11/15.

Answer: 3/5 + 2/15 = 11/15.

If in the example not 2, but 3 or more fractions are added or subtracted, then the NCD must be searched for as many fractions as are given.

Calculate: 1/2 – 5/12 + 3/6

Solution (sequence of actions):

Finding the lowest common denominator. The minimum number divisible by 2, 12 and 6 is 12.
We get: 1/2 – 5/12 + 3/6 = ?/12.
We are looking for additional multipliers. For 1/2 – 6; for 5/12 – 1; for 3/6 – 2.
We multiply by the numerators and assign the corresponding signs: 1/2 – 5/12 + 3/6 = (1*6 – 5*1 + 2*3)/12 = 7/12.

Answer: 1/2 – 5/12 + 3/6 = 7/12.

In this lesson we will look at reducing fractions to a common denominator and solve problems on this topic. Let us define the concept of a common denominator and an additional factor, recall the mutual prime numbers. Let's define the concept of the lowest common denominator (LCD) and solve a number of problems to find it.

Topic: Adding and subtracting fractions with different denominators

Lesson: Reducing fractions to a common denominator

Repetition. The main property of a fraction.

If the numerator and denominator of a fraction are multiplied or divided by the same natural number, then you get a fraction equal to it.

For example, the numerator and denominator of a fraction can be divided by 2. We get the fraction. This operation is called fraction reduction. You can also perform the inverse transformation by multiplying the numerator and denominator of the fraction by 2. In this case, we say that we have reduced the fraction to a new denominator. The number 2 is called an additional factor.

Conclusion. A fraction can be reduced to any denominator that is a multiple of the denominator of the given fraction. To bring a fraction to a new denominator, its numerator and denominator are multiplied by an additional factor.

1. Reduce the fraction to the denominator 35.

The number 35 is a multiple of 7, that is, 35 is divisible by 7 without a remainder. This means that this transformation is possible. Let's find an additional factor. To do this, divide 35 by 7. We get 5. Multiply the numerator and denominator of the original fraction by 5.

2. Reduce the fraction to denominator 18.

Let's find an additional factor. To do this, let's divide new denominator to the original one. We get 3. Multiply the numerator and denominator of this fraction by 3.

3. Reduce the fraction to a denominator of 60.

Dividing 60 by 15 gives an additional factor. It is equal to 4. Multiply the numerator and denominator by 4.

4. Reduce the fraction to the denominator 24

In simple cases, reduction to a new denominator is performed mentally. It is only customary to indicate the additional factor behind a bracket slightly to the right and above the original fraction.

A fraction can be reduced to a denominator of 15 and a fraction can be reduced to a denominator of 15. Fractions also have a common denominator of 15.

The common denominator of fractions can be any common multiple of their denominators. For simplicity, fractions are reduced to their lowest common denominator. It is equal to the least common multiple of the denominators of the given fractions.

Example. Reduce the fractions and to the lowest common denominator.

First, let's find the least common multiple of the denominators of these fractions. This number is 12. Let's find an additional factor for the first and second fractions. To do this, divide 12 by 4 and 6. Three is an additional factor for the first fraction, and two is for the second. Let's bring the fractions to the denominator 12.

We brought the fractions to a common denominator, that is, we found equal fractions that have the same denominator.

Rule. To reduce fractions to their lowest common denominator, you must

First, find the least common multiple of the denominators of these fractions, it will be their least common denominator;

Secondly, divide the lowest common denominator by the denominators of these fractions, i.e. find an additional factor for each fraction.

Third, multiply the numerator and denominator of each fraction by its additional factor.

a) Reduce the fractions and to a common denominator.

The lowest common denominator is 12. The additional factor for the first fraction is 4, for the second - 3. We reduce the fractions to the denominator 24.

b) Reduce the fractions and to a common denominator.

The lowest common denominator is 45. Dividing 45 by 9 by 15 gives 5 and 3, respectively. We reduce the fractions to the denominator 45.

c) Reduce the fractions and to a common denominator.

The common denominator is 24. Additional factors are 2 and 3, respectively.

Sometimes it can be difficult to verbally find the least common multiple of the denominators of given fractions. Then the common denominator and additional factors are found by decomposing into prime factors.

Reduce the fractions and to a common denominator.

Let's factor the numbers 60 and 168 into prime factors. Let's write out the expansion of the number 60 and add the missing factors 2 and 7 from the second expansion. Let's multiply 60 by 14 and get a common denominator of 840. The additional factor for the first fraction is 14. The additional factor for the second fraction is 5. Let's bring the fractions to a common denominator of 840.

Bibliography

1. Vilenkin N.Ya., Zhokhov V.I., Chesnokov A.S. and others. Mathematics 6. - M.: Mnemosyne, 2012.

2. Merzlyak A.G., Polonsky V.V., Yakir M.S. Mathematics 6th grade. - Gymnasium, 2006.

3. Depman I.Ya., Vilenkin N.Ya. Behind the pages of a mathematics textbook. - Enlightenment, 1989.

4. Rurukin A.N., Tchaikovsky I.V. Assignments for the mathematics course for grades 5-6. - ZSh MEPhI, 2011.

5. Rurukin A.N., Sochilov S.V., Tchaikovsky K.G. Mathematics 5-6. A manual for 6th grade students at the MEPhI correspondence school. - ZSh MEPhI, 2011.

6. Shevrin L.N., Gein A.G., Koryakov I.O. and others. Mathematics: Textbook-interlocutor for grades 5-6 high school. Math teacher's library. - Enlightenment, 1989.

You can download the books specified in clause 1.2. of this lesson.

Homework

Vilenkin N.Ya., Zhokhov V.I., Chesnokov A.S. and others. Mathematics 6. - M.: Mnemosyne, 2012. (link see 1.2)

Homework: No. 297, No. 298, No. 300.

Other tasks: No. 270, No. 290

Criss-cross multiplication

Common Divisor Method

Task. Find the meanings of the expressions:

To appreciate how much of a difference the least common multiple method makes, try calculating these same examples using the criss-cross method.

Common denominator of fractions

Of course, without a calculator. I think after this comments will be unnecessary.

See also:

I originally wanted to include common denominator techniques in the Adding and Subtracting Fractions section. But there was so much information, and its importance was so great (after all, not only numerical fractions), that it is better to study this issue separately.

So, let's say we have two fractions with different denominators. And we want to make sure that the denominators become the same. The basic property of a fraction comes to the rescue, which, let me remind you, sounds like this:

A fraction will not change if its numerator and denominator are multiplied by the same number other than zero.

Thus, if you choose the factors correctly, the denominators of the fractions will become equal - this process is called. And the required numbers, “evening out” the denominators, are called.

Why do we need to reduce fractions to a common denominator? Here are just a few reasons:

Adding and subtracting fractions with different denominators. There is no other way to perform this operation;
Comparing fractions. Sometimes reduction to a common denominator greatly simplifies this task;
Solving problems involving fractions and percentages. Percentages are, in fact, ordinary expressions that contain fractions.

There are many ways to find numbers that, when multiplied by them, will make the denominators of fractions equal. We will consider only three of them - in order of increasing complexity and, in a sense, effectiveness.

Criss-cross multiplication

The simplest and reliable way, which is guaranteed to equalize the denominators. We will act “in a headlong manner”: we multiply the first fraction by the denominator of the second fraction, and the second by the denominator of the first. As a result, the denominators of both fractions will become equal to the product of the original denominators. Take a look:

Task. Find the meanings of the expressions:

As additional factors, consider the denominators of neighboring fractions. We get:

Yes, it's that simple. If you are just starting to study fractions, it is better to work using this method - this way you will insure yourself against many mistakes and are guaranteed to get the result.

The only drawback this method- you have to do a lot of counting, because the denominators are multiplied “over and over”, and the result can be very large numbers. This is the price to pay for reliability.

Common Divisor Method

This technique helps to significantly reduce calculations, but, unfortunately, it is used quite rarely. The method is as follows:

Before you go straight ahead (i.e., using the criss-cross method), take a look at the denominators. Perhaps one of them (the one that is larger) is divided into the other.
The number resulting from this division will be an additional factor for the fraction with a smaller denominator.
In this case, a fraction with a large denominator does not need to be multiplied by anything at all - this is where the savings lie. At the same time, the probability of error is sharply reduced.

Task. Find the meanings of the expressions:

Note that 84: 21 = 4; 72: 12 = 6. Since in both cases one denominator is divided without a remainder by the other, we use the method of common factors. We have:

Note that the second fraction was not multiplied by anything at all. In fact, we cut the amount of computation in half!

By the way, I didn’t take the fractions in this example by chance. If you're interested, try counting them using the criss-cross method. After reduction, the answers will be the same, but there will be much more work.

This is the strength of the method common divisors, but, I repeat, it can only be used in the case when one of the denominators is divided by the other without a remainder. Which happens quite rarely.

Least common multiple method

When we reduce fractions to a common denominator, we are essentially trying to find a number that is divisible by each denominator. Then we bring the denominators of both fractions to this number.

There are a lot of such numbers, and the smallest of them will not necessarily be equal to the direct product of the denominators of the original fractions, as is assumed in the “criss-cross” method.

For example, for denominators 8 and 12, the number 24 is quite suitable, since 24: 8 = 3; 24: 12 = 2. This number is much less than the product 8 12 = 96.

Smallest number, which is divisible by each of the denominators, is called their (LCM).

Notation: The least common multiple of a and b is denoted LCM(a; b). For example, LCM(16, 24) = 48; LCM(8; 12) = 24.

If you manage to find such a number, the total amount of calculations will be minimal. Look at the examples:

How to Find the Lowest Common Denominator

Find the meanings of the expressions:

Note that 234 = 117 2; 351 = 117 · 3. Factors 2 and 3 are coprime (have no common factors other than 1), and factor 117 is common. Therefore LCM(234, 351) = 117 2 3 = 702.

Likewise, 15 = 5 3; 20 = 5 · 4. Factors 3 and 4 are coprime, and factor 5 is common. Therefore LCM(15, 20) = 5 3 4 = 60.

Now let's bring the fractions to common denominators:

Notice how useful it was to factorize the original denominators:

Having discovered identical factors, we immediately arrived at the least common multiple, which, generally speaking, is a non-trivial problem;
From the resulting expansion you can find out which factors are “missing” in each fraction. For example, 234 · 3 = 702, therefore, for the first fraction the additional factor is 3.

Don't think that there are such complex fractions will not be the case in real examples. They meet all the time, and the above tasks are not the limit!

The only problem is how to find this very NOC. Sometimes everything can be found in a few seconds, literally “by eye,” but in general this is a complex computational task that requires separate consideration. We won't touch on that here.

See also:

Reducing fractions to a common denominator

I originally wanted to include common denominator techniques in the Adding and Subtracting Fractions section. But there turned out to be so much information, and its importance is so great (after all, not only numerical fractions have common denominators), that it is better to study this issue separately.

A fraction will not change if its numerator and denominator are multiplied by the same number other than zero.

Thus, if you choose the factors correctly, the denominators of the fractions will become equal - this process is called. And the required numbers, “evening out” the denominators, are called.

Why do we need to reduce fractions to a common denominator?

Common denominator, concept and definition.

Here are just a few reasons:

Adding and subtracting fractions with different denominators. There is no other way to perform this operation;
Comparing fractions. Sometimes reduction to a common denominator greatly simplifies this task;
Solving problems involving fractions and percentages. Percentages are essentially ordinary expressions that contain fractions.

Criss-cross multiplication

The simplest and most reliable method, which is guaranteed to equalize the denominators. We will act “in a headlong manner”: we multiply the first fraction by the denominator of the second fraction, and the second by the denominator of the first. As a result, the denominators of both fractions will become equal to the product of the original denominators. Take a look:

Task. Find the meanings of the expressions:

As additional factors, consider the denominators of neighboring fractions. We get:

The only drawback of this method is that you have to count a lot, because the denominators are multiplied “all the way”, and the result can be very large numbers. This is the price to pay for reliability.

Common Divisor Method

This technique helps to significantly reduce calculations, but, unfortunately, it is used quite rarely. The method is as follows:

Before you go straight ahead (i.e., using the criss-cross method), take a look at the denominators. Perhaps one of them (the one that is larger) is divided into the other.
The number resulting from this division will be an additional factor for the fraction with a smaller denominator.
In this case, a fraction with a large denominator does not need to be multiplied by anything at all - this is where the savings lie. At the same time, the probability of error is sharply reduced.

Task. Find the meanings of the expressions:

Note that 84: 21 = 4; 72: 12 = 6. Since in both cases one denominator is divided without a remainder by the other, we use the method of common factors. We have:

Note that the second fraction was not multiplied by anything at all. In fact, we cut the amount of computation in half!

This is the power of the common divisors method, but, again, it can only be used when one of the denominators is divided by the other without a remainder. Which happens quite rarely.

Least common multiple method

When we reduce fractions to a common denominator, we are essentially trying to find a number that is divisible by each denominator. Then we bring the denominators of both fractions to this number.

For example, for denominators 8 and 12, the number 24 is quite suitable, since 24: 8 = 3; 24: 12 = 2. This number is much less than the product 8 12 = 96.

The smallest number that is divisible by each of the denominators is called their (LCM).

Notation: The least common multiple of a and b is denoted LCM(a; b). For example, LCM(16, 24) = 48; LCM(8; 12) = 24.

If you manage to find such a number, the total amount of calculations will be minimal. Look at the examples:

Task. Find the meanings of the expressions:

Note that 234 = 117 2; 351 = 117 · 3. Factors 2 and 3 are coprime (have no common factors other than 1), and factor 117 is common. Therefore LCM(234, 351) = 117 2 3 = 702.

Likewise, 15 = 5 3; 20 = 5 · 4. Factors 3 and 4 are coprime, and factor 5 is common. Therefore LCM(15, 20) = 5 3 4 = 60.

Now let's bring the fractions to common denominators:

Notice how useful it was to factorize the original denominators:

Having discovered identical factors, we immediately arrived at the least common multiple, which, generally speaking, is a non-trivial problem;
From the resulting expansion you can find out which factors are “missing” in each fraction. For example, 234 · 3 = 702, therefore, for the first fraction the additional factor is 3.

To appreciate how much of a difference the least common multiple method makes, try calculating these same examples using the criss-cross method. Of course, without a calculator. I think after this comments will be unnecessary.

Don't think that there won't be such complex fractions in the real examples. They meet all the time, and the above tasks are not the limit!

See also:

Reducing fractions to a common denominator

A fraction will not change if its numerator and denominator are multiplied by the same number other than zero.

Thus, if you choose the factors correctly, the denominators of the fractions will become equal - this process is called. And the required numbers, “evening out” the denominators, are called.

Why do we need to reduce fractions to a common denominator? Here are just a few reasons:

Adding and subtracting fractions with different denominators. There is no other way to perform this operation;
Comparing fractions. Sometimes reduction to a common denominator greatly simplifies this task;
Solving problems involving fractions and percentages. Percentages are essentially ordinary expressions that contain fractions.

Criss-cross multiplication

Take a look:

Task. Find the meanings of the expressions:

As additional factors, consider the denominators of neighboring fractions. We get:

Common Divisor Method

This technique helps to significantly reduce calculations, but, unfortunately, it is used quite rarely. The method is as follows:

Before you go straight ahead (i.e., using the criss-cross method), take a look at the denominators. Perhaps one of them (the one that is larger) is divided into the other.
The number resulting from this division will be an additional factor for the fraction with a smaller denominator.
In this case, a fraction with a large denominator does not need to be multiplied by anything at all - this is where the savings lie. At the same time, the probability of error is sharply reduced.

Task. Find the meanings of the expressions:

Note that 84: 21 = 4; 72: 12 = 6. Since in both cases one denominator is divided without a remainder by the other, we use the method of common factors. We have:

Note that the second fraction was not multiplied by anything at all. In fact, we cut the amount of computation in half!

This is the power of the common divisors method, but, again, it can only be used when one of the denominators is divided by the other without a remainder. Which happens quite rarely.

Least common multiple method

When we reduce fractions to a common denominator, we are essentially trying to find a number that is divisible by each denominator. Then we bring the denominators of both fractions to this number.

For example, for denominators 8 and 12, the number 24 is quite suitable, since 24: 8 = 3; 24: 12 = 2. This number is much less than the product 8 12 = 96.

The smallest number that is divisible by each of the denominators is called their (LCM).

Notation: The least common multiple of a and b is denoted LCM(a; b). For example, LCM(16, 24) = 48; LCM(8; 12) = 24.

If you manage to find such a number, the total amount of calculations will be minimal. Look at the examples:

Task. Find the meanings of the expressions:

Note that 234 = 117 2; 351 = 117 · 3. Factors 2 and 3 are coprime (have no common factors other than 1), and factor 117 is common. Therefore LCM(234, 351) = 117 2 3 = 702.

Likewise, 15 = 5 3; 20 = 5 · 4. Factors 3 and 4 are coprime, and factor 5 is common. Therefore LCM(15, 20) = 5 3 4 = 60.

Now let's bring the fractions to common denominators:

Notice how useful it was to factorize the original denominators:

Having discovered identical factors, we immediately arrived at the least common multiple, which, generally speaking, is a non-trivial problem;
From the resulting expansion you can find out which factors are “missing” in each fraction. For example, 234 · 3 = 702, therefore, for the first fraction the additional factor is 3.

Don't think that there won't be such complex fractions in the real examples. They meet all the time, and the above tasks are not the limit!

See also:

Reducing fractions to a common denominator

A fraction will not change if its numerator and denominator are multiplied by the same number other than zero.

Thus, if you choose the factors correctly, the denominators of the fractions will become equal - this process is called. And the required numbers, “evening out” the denominators, are called.

Why do we need to reduce fractions to a common denominator? Here are just a few reasons:

Adding and subtracting fractions with different denominators. There is no other way to perform this operation;
Comparing fractions. Sometimes reduction to a common denominator greatly simplifies this task;
Solving problems involving fractions and percentages. Percentages are essentially ordinary expressions that contain fractions.

Criss-cross multiplication

Task. Find the meanings of the expressions:

As additional factors, consider the denominators of neighboring fractions. We get:

The only drawback of this method is that you have to count a lot, because the denominators are multiplied “all the way”, and the result can be very large numbers.

Reducing fractions to a common denominator

This is the price to pay for reliability.

Common Divisor Method

This technique helps to significantly reduce calculations, but, unfortunately, it is used quite rarely. The method is as follows:

Before you go straight ahead (i.e., using the criss-cross method), take a look at the denominators. Perhaps one of them (the one that is larger) is divided into the other.
The number resulting from this division will be an additional factor for the fraction with a smaller denominator.
In this case, a fraction with a large denominator does not need to be multiplied by anything at all - this is where the savings lie. At the same time, the probability of error is sharply reduced.

Task. Find the meanings of the expressions:

Note that 84: 21 = 4; 72: 12 = 6. Since in both cases one denominator is divided without a remainder by the other, we use the method of common factors. We have:

Note that the second fraction was not multiplied by anything at all. In fact, we cut the amount of computation in half!

This is the power of the common divisors method, but, again, it can only be used when one of the denominators is divided by the other without a remainder. Which happens quite rarely.

Least common multiple method

When we reduce fractions to a common denominator, we are essentially trying to find a number that is divisible by each denominator. Then we bring the denominators of both fractions to this number.

For example, for denominators 8 and 12, the number 24 is quite suitable, since 24: 8 = 3; 24: 12 = 2. This number is much less than the product 8 12 = 96.

The smallest number that is divisible by each of the denominators is called their (LCM).

Notation: The least common multiple of a and b is denoted LCM(a; b). For example, LCM(16, 24) = 48; LCM(8; 12) = 24.

If you manage to find such a number, the total amount of calculations will be minimal. Look at the examples:

Task. Find the meanings of the expressions:

Note that 234 = 117 2; 351 = 117 · 3. Factors 2 and 3 are coprime (have no common factors other than 1), and factor 117 is common. Therefore LCM(234, 351) = 117 2 3 = 702.

Likewise, 15 = 5 3; 20 = 5 · 4. Factors 3 and 4 are coprime, and factor 5 is common. Therefore LCM(15, 20) = 5 3 4 = 60.

Now let's bring the fractions to common denominators:

Notice how useful it was to factorize the original denominators:

Having discovered identical factors, we immediately arrived at the least common multiple, which, generally speaking, is a non-trivial problem;
From the resulting expansion you can find out which factors are “missing” in each fraction. For example, 234 · 3 = 702, therefore, for the first fraction the additional factor is 3.

Don't think that there won't be such complex fractions in the real examples. They meet all the time, and the above tasks are not the limit!

A fraction will not change if its numerator and denominator are multiplied by the same number other than zero.

Thus, if you choose the factors correctly, the denominators of the fractions will become equal - this process is called reduction to a common denominator. And the required numbers, “evening out” the denominators, are called additional factors.

Why do we need to reduce fractions to a common denominator? Here are just a few reasons:

Adding and subtracting fractions with different denominators. There is no other way to perform this operation;
Comparing fractions. Sometimes reduction to a common denominator greatly simplifies this task;
Solving problems involving fractions and percentages. Percentages are essentially ordinary expressions that contain fractions.

Criss-cross multiplication

As additional factors, consider the denominators of neighboring fractions. We get:

Common Divisor Method

This technique helps to significantly reduce calculations, but, unfortunately, it is used quite rarely. The method is as follows:

Before you go straight ahead (i.e., using the criss-cross method), take a look at the denominators. Perhaps one of them (the one that is larger) is divided into the other.
The number resulting from this division will be an additional factor for the fraction with a smaller denominator.
In this case, a fraction with a large denominator does not need to be multiplied by anything at all - this is where the savings lie. At the same time, the probability of error is sharply reduced.

Task. Find the meanings of the expressions:

Note that 84: 21 = 4; 72: 12 = 6. Since in both cases one denominator is divided without a remainder by the other, we use the method of common factors. We have:

Note that the second fraction was not multiplied by anything at all. In fact, we cut the amount of computation in half!

This is the power of the common divisors method, but, again, it can only be used when one of the denominators is divided by the other without a remainder. Which happens quite rarely.

Reducing fractions to the lowest common denominator, rules, examples, solutions.

This article explains how to find the lowest common denominator And how to reduce fractions to a common denominator.

First, the definitions of common denominator of fractions and least common denominator are given, and it is shown how to find the common denominator of fractions. Below is a rule for reducing fractions to a common denominator and examples of the application of this rule are considered. In conclusion, examples of bringing three and more fractions to a common denominator.

What is called reducing fractions to a common denominator?

If ordinary fractions have equal denominators, then these fractions are said to be reduced to a common denominator.

Thus, the fractions 45/76 and 143/76 are reduced to a common denominator of 76, and the fractions 1/3, 3/3, 17/3 and 1,000/3 are reduced to a common denominator of 3.

If the denominators of the fractions are not equal, then such fractions can always be reduced to a common denominator by multiplying their numerator and denominator by certain additional factors.

For example, ordinary fractions 2/5 and 7/4 with the help of additional factors 4 and 5, respectively, are reduced to a common denominator 20. Indeed, multiplying the numerator and denominator of the fraction 2/5 by 4, we obtain the fraction 8/20, and multiplying the numerator and denominator fractions 7/4 by 5, we arrive at the fraction 35/20 (see bringing fractions to a new denominator).

Now we can say what it is to reduce fractions to a common denominator. Reducing fractions to a common denominator- This is the multiplication of the numerators and denominators of given fractions by such additional factors that the result is fractions with the same denominators.

Top of page

Common denominator, definition, examples

Now it's time to define the common denominator of fractions.

In other words, the common denominator of a certain set of ordinary fractions is any natural number that is divisible by all the denominators of these fractions.

From the stated definition it follows that this set of fractions has infinitely many common denominators, since there is infinite set common multiples of all denominators of the original set of fractions.

Determining the common denominator of fractions allows you to find the common denominators of given fractions. Let, for example, given the fractions 1/4 and 5/6, their denominators are 4 and 6, respectively.

Positive common multiples of 4 and 6 are 12, 24, 36, 48, ... Any of these numbers is a common denominator of the fractions 1/4 and 5/6.

To consolidate the material, consider the solution to the following example.

Can the fractions 2/3, 23/6 and 7/12 be reduced to a common denominator of 150?

To answer the question posed, we need to find out whether the number 150 is a common multiple of the denominators 3, 6 and 12. To do this, we will check whether 150 is divisible by each of these numbers (if necessary, see the rules and examples of dividing natural numbers, as well as the rules and examples of dividing natural numbers with a remainder): 150:3=50, 150:6=25, 150:12=12 (rest.

So, 150 is not evenly divisible by 12, therefore 150 is not a common multiple of 3, 6 and 12. Therefore, the number 150 cannot be a common denominator of the original fractions.

Top of page

Lowest common denominator, how to find it?

In the set of numbers that are the common denominators of given fractions, there is a smallest natural number, which is called the least common denominator.

Let us formulate the definition of the lowest common denominator of these fractions.

It remains to deal with the question of how to find the least common divisor.

Since the least common multiple is the least positive common divisor of a given set of numbers, the LCM of the denominators of the given fractions is the least common denominator of the given fractions.

Thus, finding the least common denominator of fractions comes down to finding the LCM of the denominators of these fractions.

Let's look at the solution to the example.

Find the lowest common denominator of the fractions 3/10 and 277/28.

The denominators of these fractions are 10 and 28. The desired least common denominator is found as the LCM of the numbers 10 and 28. In our case, it is easy to find the LCM by factoring the numbers into prime factors: since 10 = 2 5, and 28 = 2 2 7 , then LCM(15, 28)=2·2·5·7=140.

Top of page

How to reduce fractions to a common denominator? Rule, examples, solutions

Common fractions usually result in a lowest common denominator.

We will now write down a rule that explains how to reduce fractions to their lowest common denominator.

Rule for reducing fractions to lowest common denominator consists of three steps:

First, find the lowest common denominator of the fractions.
Second, an additional factor is calculated for each fraction by dividing the lowest common denominator by the denominator of each fraction.
Third, the numerator and denominator of each fraction are multiplied by its additional factor.

Let us apply the stated rule to solve the following example.

Reduce the fractions 5/14 and 7/18 to their lowest common denominator.

Let's perform all the steps of the algorithm for reducing fractions to the lowest common denominator.

First, we find the least common denominator, which is equal to the least common multiple of the numbers 14 and 18. Since 14=2·7 and 18=2·3·3, then LCM(14, 18)=2·3·3·7=126.

Now we calculate additional factors with the help of which the fractions 5/14 and 7/18 will be reduced to a denominator of 126. For the fraction 5/14 the additional factor is 126:14=9, and for the fraction 7/18 the additional factor is 126:18=7 .

It remains to multiply the numerators and denominators of the fractions 5/14 and 7/18 by additional factors 9 and 7, respectively.

We have And .

So, reducing the fractions 5/14 and 7/18 to the lowest common denominator is complete.

The resulting fractions were 45/126 and 49/126.

Top of page

Reducing three or more fractions to the lowest common denominator

The rule from the previous paragraph allows you to reduce not only two fractions, but also three fractions, and more of them, to the lowest common denominator.

Let's look at the example solution.

Bring four common fractions 3/2, 5/6, 3/8 and 17/18 to the lowest common denominator.

The least common denominator of these fractions is equal to the least common multiple of the numbers 2, 6, 8 and 18. To find the LCM(2, 6, 8, 18) we use the information from the section Finding the LCM of three or more numbers.

We get LCM(2, 6)=6, LCM(6, 8)=24, finally LCM(24, 18)=72, therefore LCM(2, 6, 8, 18)=72. So the lowest common denominator is 72.

Now we calculate additional factors. For the fraction 3/2 the additional factor is 72:2=36, for the fraction 5/6 it is 72:6=12, for the fraction 3/8 the additional factor is 72:8=9, and for the fraction 17/18 it is 72 :18=4.

Reducing fractions to a common denominator

There is one last step left in reducing the original fractions to the lowest common denominator: .

Top of page

Common denominator is any positive common multiple of all denominators of these fractions.

Lowest common denominator is the smallest number of all the common denominators of these fractions.

Vilenkin N.Ya., Zhokhov V.I., Chesnokov A.S., Shvartsburd S.I. Mathematics: textbook for 5th grade. educational institutions.
Vilenkin N.Ya. and others. Mathematics. 6th grade: textbook for general education institutions.

Common denominator of common fractions

If ordinary fractions have the same denominators, then these fractions have a common denominator. Eg,

they have a common denominator.

Common denominator This is a number that is the denominator for two or more regular fractions.

Fractions with different denominators can be reduced to a common denominator.

Providing fractions with a common denominator

Providing fractions with a common denominator Is replacing these fractions with different denominators the same fractions with the same denominators?

Fractions can simply be reduced to a common denominator or lowest common denominator.

Lowest common denominator This is the lowest common denominator of these fractions.

Common denominator of factions on the Internet

To give fractions the lowest common denominator, you need:

If possible, perform a fraction reduction.
Find the smallest shared directories these fractions. NOC will be their lowest common denominator.
Divide the LCM by the denominators of these fractions. This measure finds an additional factor for each of these fractions. Additional coefficient Is it a number that requires the members of a fraction to be multiplied to bring it to a common denominator?
Multiply the numerator and denominator of each fraction with an additional factor.

Example.

1) Find the NOC names of these factions:

NOC(8, 12) = 24

2) Additional factors were found:

24: 8 = 3 (for ) and 24: 12 = 2 (for )

3) Multiply the members of each faction with an additional factor:

Decreasing the common denominator can be written in a shorter form by specifying an additional factor in addition to each fraction's counter (top right or top left) and not writing down the intermediate calculations:

The common denominator can be reduced more easily by multiplying the members of the first fraction with the second immanent share and the members of the second fraction with the denominator of the first.

Example. Get the common denominator of fractions and:

The product of their denominators can be taken as the common denominator of fractions.

Reducing fractions to a common denominator is used to add, subtract, and compare fractions with different denominators.

Reduction to common denominator calculator

This calculator will help you reduce common fractions to the lowest common denominator.

Just enter two fractions and click.

5.4.5. Examples of converting fractions to the lowest common denominator

The lowest common denominator of continued fractions is the lowest common denominator for those fractions. ( see section “Finding the least common multiple”: 5.3.5. Find the least number of multiples (NOC) of the given numbers).

To reduce the fraction by the lowest common denominator, you need to: 1) find the least common multiple of the denominators of these fractions, and this will be the lowest common denominator.

2) finds an additional coefficient for each of the fractions, for which a new denominator is distributed with the name of each fraction. 3) multiply the numerator and denominator of each fraction with an additional factor.

Examples. To reduce the following fractions to the lowest common denominator.

We find the least common multi-digit denominator: LCM (5; 4) = 20, since 20 is the smallest number divided by 5 and 4.

For the first part, an additional coefficient of 4 (20 : 5 = 4). For the second fraction there is an additional coefficient of 5 (20 : 4 = 5). Multiply the number and denominator of the first fraction by 4, and the counter and denominator of the second fraction by 5.

20 ).

The lowest common denominator for these fractions is the number 8, since it is divisible by 4 and internally.

For the first fraction there is no additional factor (or we can say that it is equal to one), the second factor is an additional factor 2 (8 : 4 = 2). Multiply the numerator and denominator of the second fraction by 2.

Online calculator. Providing fractions with a common denominator

We have reduced these fractions to the lowest common denominator ( 8th place).

These factions are not intolerable.

The first faction was reduced by 4, and the second faction was reduced by 2. (See Examples for reducing common factions: Sitemap → 5.4.2.

Examples of reduction of common fractions). Finds NOC (16 ; 20) = 24· 5 = 16· 5 = 80. An additional factor for the 1st fraction is 5 (80 : 16 = 5). An additional factor for the second fraction is 4 (80 : 20 = 4).

We multiply the numerator and denominator of the first fraction with 5, and the counter and denominator of the second fraction with 4. The fractional information was given to the lowest common denominator ( 80 ).

Find the lowest common denominator of NOx (5 ; 6 and 15) = NOK (5 ; 6 and 15) = 30. An additional factor for the first fraction is 6 (30 : 5 = 6), is an additional factor in the second part of 5 (30 : 6 = 5), is an additional factor for the third fraction 2 (30 : 15 = 2).

The count and denominator of the first fraction are multiplied by 6, the count and denominator of the second fraction by 5, and the count and denominator of the third fraction by 2. The partial data was given the least common denominator 30 ).

Page 1 of 11

Lowest common denominator.

What is the lowest common denominator?

Definition:
Lowest common denominator is the smallest positive number that is a multiple of the denominators of these fractions.

How to reduce to the lowest common denominator? To answer this question, consider an example:

Reduce fractions with unlike denominators to their lowest common denominator.

Solution:
To find the lowest common denominator, you need to find the least common multiple (LCM) of the denominators of these fractions.

The first fraction has a denominator of 20; let’s factor it into prime factors.
20=2⋅5⋅2

Let us also decompose the second denominator of the fraction 14 into prime factors.
14=7⋅2

NOC(14,20)= 2⋅5⋅2⋅7=140

Answer: The lowest common denominator would be 140.

How to reduce a fraction to a common denominator?

You need to multiply the first fraction \(\frac(1)(20)\) by 7 to get a denominator of 140.

\(\frac(1)(20)=\frac(1 \times 7)(20 \times 7)=\frac(7)(140)\)
And multiply the second fraction by 10.

\(\frac(3)(14)=\frac(3 \times 10)(14 \times 10)=\frac(30)(140)\)

Rules or algorithm for reducing fractions to a common denominator.

Algorithm for reducing fractions to the lowest common denominator:

You need to factor the denominators of fractions into prime factors.
We need to find the least common multiple (LCM) for the denominators of these fractions.
Reduce fractions to a common denominator, that is, multiply both the numerator and denominator of the fraction by a factor.

Common denominator for several fractions.

How to find the common denominator for several fractions?

Let's look at an example:
Find the lowest common denominator for the fractions \(\frac(2)(11), \frac(1)(15), \frac(3)(22)\)

Solution:
Let's factor the denominators 11, 15 and 22 into prime factors.

The number 11 is already a simple number in itself, so there is no need to describe it.
Let's expand the number 15=5⋅3
Let's expand the number 22=11⋅2

Find the least common multiple (LCM) of the denominators 11, 15, and 22.
LCM(11, 15, 22)=11⋅2⋅5⋅3=330

We have found the lowest common denominator for these fractions. Now let's bring these fractions \(\frac(2)(11), \frac(1)(15), \frac(3)(22)\) to a common denominator equal to 330.

\(\begin(align)
\frac(2)(11)=\frac(2 \times 30)(11 \times 30)=\frac(60)(330) \\\\
\frac(1)(15)=\frac(1 \times 22)(15 \times 22)=\frac(22)(330) \\\\
\frac(3)(22)=\frac(3 \times 15)(22 \times 15)=\frac(60)(330) \\\\
\end(align)\)

A fraction will not change if its numerator and denominator are multiplied by the same number other than zero.

Why do we need to reduce fractions to a common denominator? Here are just a few reasons:

Adding and subtracting fractions with different denominators. There is no other way to perform this operation;
Comparing fractions. Sometimes reduction to a common denominator greatly simplifies this task;
Solving problems involving fractions and percentages. Percentages are essentially ordinary expressions that contain fractions.

Criss-cross multiplication

As additional factors, consider the denominators of neighboring fractions. We get:

Common Divisor Method

This technique helps to significantly reduce calculations, but, unfortunately, it is used quite rarely. The method is as follows:

Before you go straight ahead (i.e., using the criss-cross method), take a look at the denominators. Perhaps one of them (the one that is larger) is divided into the other.
The number resulting from this division will be an additional factor for the fraction with a smaller denominator.
In this case, a fraction with a large denominator does not need to be multiplied by anything at all - this is where the savings lie. At the same time, the probability of error is sharply reduced.

Task. Find the meanings of the expressions:

Note that 84: 21 = 4; 72: 12 = 6. Since in both cases one denominator is divided without a remainder by the other, we use the method of common factors. We have:

Note that the second fraction was not multiplied by anything at all. In fact, we cut the amount of computation in half!

This is the power of the common divisors method, but, again, it can only be used when one of the denominators is divided by the other without a remainder. Which happens quite rarely.

Least common multiple method

When we reduce fractions to a common denominator, we are essentially trying to find a number that is divisible by each denominator. Then we bring the denominators of both fractions to this number.

For example, for denominators 8 and 12, the number 24 is quite suitable, since 24: 8 = 3; 24: 12 = 2. This number is much less than the product 8 · 12 = 96.

The smallest number that is divisible by each of the denominators is called their least common multiple (LCM).

Notation: The least common multiple of a and b is denoted by LCM(a ; b) . For example, LCM(16, 24) = 48 ; LCM(8; 12) = 24 .

If you manage to find such a number, the total amount of calculations will be minimal. Look at the examples:

Task. Find the meanings of the expressions:

Note that 234 = 117 2; 351 = 117 3. Factors 2 and 3 are coprime (have no common factors other than 1), and factor 117 is common. Therefore LCM(234, 351) = 117 2 3 = 702.

Likewise, 15 = 5 3; 20 = 5 · 4. Factors 3 and 4 are coprime, and factor 5 is common. Therefore LCM(15, 20) = 5 3 4 = 60.

Now let's bring the fractions to common denominators:

Notice how useful it was to factorize the original denominators:

Having discovered identical factors, we immediately arrived at the least common multiple, which, generally speaking, is a non-trivial problem;
From the resulting expansion you can find out which factors are “missing” in each fraction. For example, 234 · 3 = 702, therefore, for the first fraction the additional factor is 3.

Don't think that there won't be such complex fractions in the real examples. They meet all the time, and the above tasks are not the limit!

Least common denominator (LCD) of algebraic fractions, finding it. Reducing fractions to the lowest common denominator, rule, examples, solutions

Read also

How to find the lowest common denominator - concept

How to find the lowest common denominator - examples

Criss-cross multiplication

Common Divisor Method

Common denominator of fractions

Criss-cross multiplication

Common Divisor Method

Least common multiple method

How to Find the Lowest Common Denominator

Reducing fractions to a common denominator

Common denominator, concept and definition.

Criss-cross multiplication

Common Divisor Method

Least common multiple method

Reducing fractions to a common denominator

Criss-cross multiplication

Common Divisor Method

Least common multiple method

Reducing fractions to a common denominator

Criss-cross multiplication

Reducing fractions to a common denominator

Common Divisor Method

Least common multiple method

Criss-cross multiplication

Common Divisor Method

Reducing fractions to the lowest common denominator, rules, examples, solutions.

What is called reducing fractions to a common denominator?

Common denominator, definition, examples

Lowest common denominator, how to find it?

How to reduce fractions to a common denominator? Rule, examples, solutions

Reducing three or more fractions to the lowest common denominator

Reducing fractions to a common denominator

Common denominator of common fractions

Providing fractions with a common denominator

Common denominator of factions on the Internet

Reduction to common denominator calculator

5.4.5. Examples of converting fractions to the lowest common denominator

Online calculator. Providing fractions with a common denominator

Lowest common denominator.

Rules or algorithm for reducing fractions to a common denominator.

Common denominator for several fractions.

Criss-cross multiplication

Common Divisor Method

Least common multiple method