Mechanical work is equal to the ratio. Kinetic and potential energy. Ground reaction work

« Physics - 10th grade"

The law of conservation of energy is a fundamental law of nature that allows us to describe most occurring phenomena.

Description of the movement of bodies is also possible using such concepts of dynamics as work and energy.

Remember what work and power are in physics.

Do these concepts coincide with everyday ideas about them?

All our daily actions come down to the fact that we, with the help of muscles, either set the surrounding bodies in motion and maintain this movement, or stop the moving bodies.

These bodies are tools (hammer, pen, saw), in games - balls, washers, chessmen. In production and agriculture people also set tools in motion.

The use of machines increases labor productivity many times due to the use of engines in them.

The purpose of any engine is to set bodies in motion and maintain this movement, despite braking by both ordinary friction and “working” resistance (the cutter should not just slide along the metal, but, cutting into it, remove chips; the plow should loosen land, etc.). In this case, a force must act on the moving body from the side of the engine.

Work is performed in nature whenever a force (or several forces) from another body (other bodies) acts on a body in the direction of its movement or against it.

The force of gravity does work when raindrops or stones fall from a cliff. At the same time, work is also done by the resistance force acting on the falling drops or on the stone from the air. The elastic force also performs work when a tree bent by the wind straightens.

Definition of work.

Newton's second law in impulse form Δ = Δt allows you to determine how the speed of a body changes in magnitude and direction if a force acts on it during a time Δt.

The influence of forces on bodies that lead to a change in the modulus of their velocity is characterized by a value that depends on both the forces and the movements of the bodies. In mechanics this quantity is called work of force.

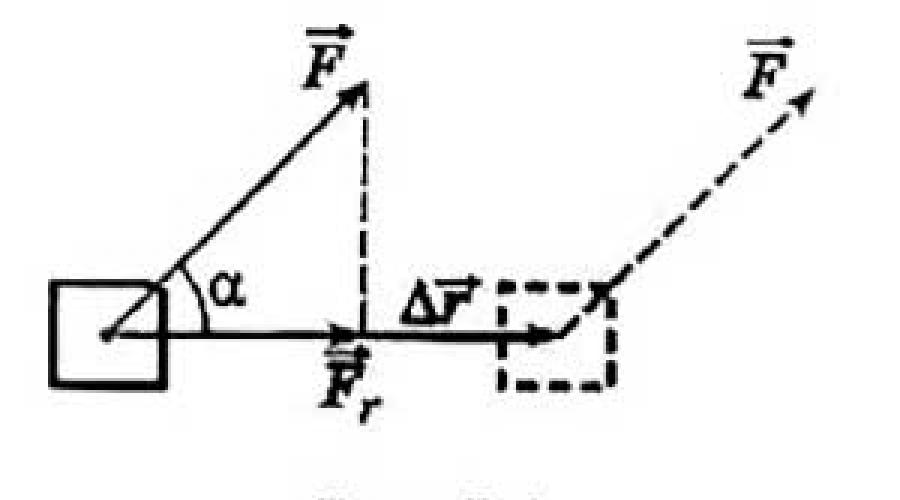
A change in speed in absolute value is possible only in the case when the projection of the force F r on the direction of movement of the body is different from zero. It is this projection that determines the action of the force that changes the velocity of the body modulo. She does the work. Therefore, work can be considered as the product of the projection of force F r by the displacement modulus |Δ| (Fig. 5.1):

A = F r |Δ|. (5.1)

If the angle between force and displacement is denoted by α, then Fr = Fcosα.

Therefore, the work is equal to:

A = |Δ|cosα. (5.2)

Our everyday idea of ​​work differs from the definition of work in physics. You are holding a heavy suitcase, and it seems to you that you are doing work. However, from a physical point of view, your work is zero.

The work of a constant force is equal to the product of the moduli of the force and the displacement of the point of application of the force and the cosine of the angle between them.

In the general case, when a rigid body moves, the displacements of its different points are different, but when determining the work of a force, we are under Δ we understand the movement of its point of application. At forward movement of a rigid body, the movement of all its points coincides with the movement of the point of application of force.

Work, unlike force and displacement, is not a vector, but a scalar quantity. It can be positive, negative or zero.

The sign of the work is determined by the sign of the cosine of the angle between force and displacement. If α< 90°, то А >0, since cosine sharp corners positive. For α > 90°, the work is negative, since the cosine of obtuse angles is negative. At α = 90° (force perpendicular to displacement) no work is done.

If several forces act on a body, then the projection of the resultant force on the displacement is equal to the sum of the projections of the individual forces:

F r = F 1r + F 2r + ... .

Therefore, for the work of the resultant force we obtain

A = F 1r |Δ| + F 2r |Δ| + ... = A 1 + A 2 + .... (5.3)

If several forces act on a body, then the total work (the algebraic sum of the work of all forces) is equal to the work of the resultant force.

The work done by a force can be represented graphically. Let us explain this by depicting in the figure the dependence of the projection of force on the coordinates of the body when it moves in a straight line.

Let the body move along the OX axis (Fig. 5.2), then

Fcosα = F x , |Δ| = Δ x.

For the work of force we get

A = F|Δ|cosα = F x Δx.

Obviously, the area of ​​the rectangle shaded in Figure (5.3, a) is numerically equal to the work done when moving a body from a point with coordinate x1 to a point with coordinate x2.

Formula (5.1) is valid in the case when the projection of the force onto the displacement is constant. In the case of a curvilinear trajectory, constant or variable force, we divide the trajectory into small segments, which can be considered rectilinear, and the projection of the force at a small displacement Δ - constant.

Unit of work.

The unit of work can be established using the basic formula (5.2). If, when moving a body per unit length, it is acted upon by a force whose modulus is equal to one, and the direction of the force coincides with the direction of movement of its point of application (α = 0), then the work will be equal to one. In the International System (SI), the unit of work is the joule (denoted by J):

1 J = 1 N 1 m = 1 N m.

Joule- this is the work done by a force of 1 N on displacement 1 if the directions of force and displacement coincide.

Multiple units of work are often used: kilojoule and megajoule:

1 kJ = 1000 J,
1 MJ = 1000000 J.

Work can be completed either in a large period of time or in a very short one. In practice, however, it is far from indifferent whether work can be done quickly or slowly. The time during which work is performed determines the performance of any engine. A tiny electric motor can do a lot of work, but it will take a lot of time. Therefore, along with work, a quantity is introduced that characterizes the speed with which it is produced - power.

Power is the ratio of work A to the time interval Δt during which this work is done, i.e. power is the speed of work:

Substituting into formula (5.4) instead of work A its expression (5.2), we obtain

Thus, if the force and speed of a body are constant, then the power is equal to the product of the magnitude of the force vector by the magnitude of the velocity vector and the cosine of the angle between the directions of these vectors. If these quantities are variable, then using formula (5.4) we can determine the average power similar to the definition average speed body movements.

The concept of power is introduced to evaluate the work per unit of time performed by any mechanism (pump, crane, machine motor, etc.). Therefore, in formulas (5.4) and (5.5), traction force is always meant.

In SI, power is expressed in watts (W).

Power is equal to 1 W if work equal to 1 J is performed in 1 s.

Along with the watt, larger (multiple) units of power are used:

1 kW (kilowatt) = 1000 W,
1 MW (megawatt) = 1,000,000 W.

Mechanical work. Units of work.

In everyday life, we understand everything by the concept of “work”.

In physics, the concept Job somewhat different. It is a definite physical quantity, which means it can be measured. In physics it is studied primarily mechanical work .

Let's look at examples of mechanical work.

The train moves under the traction force of an electric locomotive, and mechanical work is performed. When a gun is fired, the pressure force of the powder gases does work - it moves the bullet along the barrel, and the speed of the bullet increases.

From these examples it is clear that mechanical work is performed when a body moves under the influence of force. Mechanical work is also performed in the case when a force acting on a body (for example, friction force) reduces the speed of its movement.

Wanting to move the cabinet, we press hard on it, but if it does not move, then we do not perform mechanical work. One can imagine a case when a body moves without the participation of forces (by inertia); in this case, mechanical work is also not performed.

So, mechanical work is done only when a force acts on a body and it moves .

It is not difficult to understand that the greater the force acts on the body and the longer the path that the body travels under the influence of this force, the greater the work done.

Mechanical work is directly proportional to the force applied and directly proportional to the distance traveled .

Therefore, we agreed to measure mechanical work by the product of force and the path traveled along this direction of this force:

work = force × path

Where A- Job, F- strength and s- distance traveled.

A unit of work is taken to be the work done by a force of 1N over a path of 1 m.

Unit of work - joule (J ) named after the English scientist Joule. Thus,

1 J = 1N m.

Also used kilojoules (kJ) .

1 kJ = 1000 J.

Formula A = Fs applicable when the force F constant and coincides with the direction of movement of the body.

If the direction of the force coincides with the direction of motion of the body, then given power does positive work.

If the body moves in the direction opposite to the direction of the applied force, for example, the sliding friction force, then this force does negative work.

If the direction of the force acting on the body is perpendicular to the direction of movement, then this force does no work, the work is zero:

In the future, speaking about mechanical work, we will briefly call it in one word - work.

Example. Calculate the work done during lifting granite slab volume 0.5 m3 to a height of 20 m. Density of granite 2500 kg/m3.

Given:

ρ = 2500 kg/m 3

Solution:

where F is the force that must be applied to uniformly lift the slab up. This force is equal in modulus to the force Fstrand acting on the slab, i.e. F = Fstrand. And the force of gravity can be determined by the mass of the slab: Fweight = gm. Let's calculate the mass of the slab, knowing its volume and the density of granite: m = ρV; s = h, i.e. the path is equal to the lifting height.

So, m = 2500 kg/m3 · 0.5 m3 = 1250 kg.

F = 9.8 N/kg · 1250 kg ≈ 12,250 N.

A = 12,250 N · 20 m = 245,000 J = 245 kJ.

Answer: A =245 kJ.

Levers.Power.Energy

To perform the same work, different engines require different time. For example, crane at a construction site lifts it up in a few minutes top floor buildings are hundreds of bricks. If these bricks were moved by a worker, it would take him several hours to do this. Another example. A horse can plow a hectare of land in 10-12 hours, while a tractor with a multi-share plow ( ploughshare- part of the plow that cuts the layer of earth from below and transfers it to the dump; multi-ploughshare - many ploughshares), this work will be completed in 40-50 minutes.

It is clear that a crane does the same work faster than a worker, and a tractor does the same work faster than a horse. The speed of work is characterized by a special quantity called power.

Power is equal to the ratio of work to the time during which it was performed.

To calculate power, you need to divide the work by the time during which this work was done. power = work/time.

Where N- power, A- Job, t- time of work performed.

Power is a constant quantity when the same work is done every second; in other cases the ratio A/t determines the average power:

N avg = A/t . The unit of power is taken to be the power at which J of work is done in 1 s.

This unit is called the watt ( W) in honor of another English scientist, Watt.

1 watt = 1 joule/1 second, or 1 W = 1 J/s.

Watt (joule per second) - W (1 J/s).

Larger units of power are widely used in technology - kilowatt (kW), megawatt (MW) .

1 MW = 1,000,000 W

1 kW = 1000 W

1 mW = 0.001 W

1 W = 0.000001 MW

1 W = 0.001 kW

1 W = 1000 mW

Example. Find the power of the water flow flowing through the dam if the height of the water fall is 25 m and its flow rate is 120 m3 per minute.

Given:

ρ = 1000 kg/m3

Solution:

Mass of falling water: m = ρV,

m = 1000 kg/m3 120 m3 = 120,000 kg (12 104 kg).

Gravity acting on water:

F = 9.8 m/s2 120,000 kg ≈ 1,200,000 N (12 105 N)

Work done by flow per minute:

A - 1,200,000 N · 25 m = 30,000,000 J (3 · 107 J).

Flow power: N = A/t,

N = 30,000,000 J / 60 s = 500,000 W = 0.5 MW.

Answer: N = 0.5 MW.

Various engines have powers ranging from hundredths and tenths of a kilowatt (electric razor engine, sewing machine) up to hundreds of thousands of kilowatts (water and steam turbines).

Table 5.

Power of some engines, kW.

Each engine has a plate (engine passport), which indicates some information about the engine, including its power.

Human power under normal operating conditions is on average 70-80 W. When jumping or running up stairs, a person can develop power up to 730 W, and in some cases even more.

From the formula N = A/t it follows that

To calculate the work, it is necessary to multiply the power by the time during which this work was performed.

Example. The room fan motor has a power of 35 watts. How much work does he do in 10 minutes?

Let's write down the conditions of the problem and solve it.

Given:

Solution:

A = 35 W * 600s = 21,000 W * s = 21,000 J = 21 kJ.

Answer A= 21 kJ.

Simple mechanisms.

Since time immemorial, man has used various devices to perform mechanical work.

Everyone knows that heavy object(stone, cabinet, machine tool), which cannot be moved by hand, can be moved using a sufficiently long stick - a lever.

On this moment it is believed that with the help of levers three thousand years ago during the construction of the pyramids in Ancient Egypt moved and raised heavy stone slabs to great heights.

In many cases, instead of lifting a heavy load to a certain height, it can be rolled or pulled to the same height along an inclined plane or lifted using blocks.

Devices used to convert force are called mechanisms .

Simple mechanisms include: levers and its varieties - block, gate; inclined plane and its varieties - wedge, screw. In most cases simple mechanisms used to gain strength, that is, to increase the force acting on the body several times.

Simple mechanisms are found both in household and in all complex industrial and industrial machines that cut, twist and stamp large sheets of steel or draw the finest threads from which fabrics are then made. The same mechanisms can be found in modern complex automatic machines, printing and counting machines.

Lever arm. Balance of forces on the lever.

Let's consider the simplest and most common mechanism - the lever.

The lever is solid, which can rotate around a fixed support.

The pictures show how a worker uses a crowbar as a lever to lift a load. In the first case, the worker with force F presses the end of the crowbar B, in the second - raises the end B.

The worker needs to overcome the weight of the load P- force directed vertically downwards. To do this, he turns the crowbar around an axis passing through the only motionless the breaking point is the point of its support ABOUT. Force F with which the worker acts on the lever is less force P, thus the worker receives gain in strength. Using a lever, you can lift such a heavy load that you cannot lift it on your own.

The figure shows a lever whose axis of rotation is ABOUT(fulcrum) is located between the points of application of forces A And IN. Another picture shows a diagram of this lever. Both forces F 1 and F 2 acting on the lever are directed in one direction.

The shortest distance between the fulcrum and the straight line along which the force acts on the lever is called the arm of force.

The length of this perpendicular will be the arm of this force. The figure shows that OA- shoulder strength F 1; OB- shoulder strength F 2. The forces acting on the lever can rotate it around its axis in two directions: clockwise or counterclockwise. Yes, strength F 1 rotates the lever clockwise, and the force F 2 rotates it counterclockwise.

The condition under which the lever is in equilibrium under the influence of forces applied to it can be established experimentally. It must be remembered that the result of the force depends not only on its numerical value (modulus), but also on the point at which it is applied to the body, or how it is directed.

Suspended from the lever (see figure) on both sides of the fulcrum various loads so that the lever remained in balance every time. The forces acting on the lever are equal to the weights of these loads. For each case, the force modules and their shoulders are measured. From the experience shown in Figure 154, it is clear that force 2 N balances the force 4 N. In this case, as can be seen from the figure, the shoulder of lesser strength is 2 times larger than the shoulder of greater strength.

Based on such experiments, the condition (rule) of lever equilibrium was established.

A lever is in equilibrium when the forces acting on it are inversely proportional to the arms of these forces.

This rule can be written as a formula:

F 1/F 2 = l 2/ l 1 ,

Where F 1And F 2 - forces acting on the lever, l 1And l 2 , - the shoulders of these forces (see figure).

The rule of lever equilibrium was established by Archimedes around 287 - 212. BC e. (but in the last paragraph it was said that the levers were used by the Egyptians? Or does the word “established” play an important role here?)

From this rule it follows that a smaller force can be used to balance a larger force using a lever. Let one arm of the lever be 3 times larger than the other (see figure). Then, by applying a force of, for example, 400 N at point B, you can lift a stone weighing 1200 N. To lift an even heavier load, you need to increase the length of the lever arm on which the worker acts.

Example. Using a lever, a worker lifts a slab weighing 240 kg (see Fig. 149). What force does he apply to the larger lever arm of 2.4 m if the smaller arm is 0.6 m?

Let's write down the conditions of the problem and solve it.

Given:

Solution:

According to the lever equilibrium rule, F1/F2 = l2/l1, whence F1 = F2 l2/l1, where F2 = P is the weight of the stone. Stone weight asd = gm, F = 9.8 N 240 kg ≈ 2400 N

Then, F1 = 2400 N · 0.6/2.4 = 600 N.

Answer: F1 = 600 N.

In our example, the worker overcomes a force of 2400 N, applying a force of 600 N to the lever. But in this case, the arm on which the worker acts is 4 times longer than the one on which the weight of the stone acts ( l 1 : l 2 = 2.4 m: 0.6 m = 4).

By applying the rule of leverage, a smaller force can balance a larger force. In this case, the shoulder of lesser force should be longer than the shoulder of greater strength.

Moment of power.

You already know the rule of lever equilibrium:

F 1 / F 2 = l 2 / l 1 ,

Using the property of proportion (the product of its extreme members is equal to the product of its middle members), we write it in this form:

F 1l 1 = F 2 l 2 .

On the left side of the equality is the product of force F 1 on her shoulder l 1, and on the right - the product of force F 2 on her shoulder l 2 .

The product of the modulus of the force rotating the body and its shoulder is called moment of force; it is designated by the letter M. This means

A lever is in equilibrium under the action of two forces if the moment of the force rotating it clockwise is equal to the moment of the force rotating it counterclockwise.

This rule is called rule of moments , can be written as a formula:

M1 = M2

Indeed, in the experiment we considered (§ 56), the acting forces were equal to 2 N and 4 N, their shoulders respectively amounted to 4 and 2 lever pressures, i.e. the moments of these forces are the same when the lever is in equilibrium.

The moment of force, like any physical quantity, can be measured. The unit of moment of force is taken to be a moment of force of 1 N, the arm of which is exactly 1 m.

This unit is called newton meter (N m).

The moment of force characterizes the action of a force, and shows that it depends simultaneously on both the modulus of the force and its leverage. Indeed, we already know, for example, that the action of a force on a door depends both on the magnitude of the force and on where the force is applied. The easier it is to turn the door, the farther from the axis of rotation the force acting on it is applied. It’s better to unscrew the nut long wrench than short. The easier it is to lift a bucket from the well, the longer the handle of the gate, etc.

Levers in technology, everyday life and nature.

The rule of leverage (or the rule of moments) underlies the action of various kinds of tools and devices used in technology and everyday life where a gain in strength or travel is required.

We have a gain in strength when working with scissors. Scissors - this is a lever(fig), the axis of rotation of which occurs through a screw connecting both halves of the scissors. Acting force F 1 is the muscular strength of the hand of the person gripping the scissors. Counterforce F 2 is the resistance force of the material being cut with scissors. Depending on the purpose of the scissors, their design varies. Office scissors, designed for cutting paper, have long blades and handles that are almost the same length. No paper cutting required great strength, and with a long blade it is more convenient to cut in a straight line. Cutting scissors sheet metal(Fig.) have handles much longer than the blades, since the resistance force of the metal is great and to balance it, the arm of the acting force has to be significantly increased. The difference between the length of the handles and the distance of the cutting part and the axis of rotation is even greater wire cutters(Fig.), designed for cutting wire.

Levers various types available on many cars. The handle of a sewing machine, the pedals or handbrake of a bicycle, the pedals of a car and tractor, and the keys of a piano are all examples of levers used in these machines and tools.

Examples of the use of levers are the handles of vices and workbenches, the lever drilling machine etc.

The action of lever scales is based on the principle of the lever (Fig.). The training scales shown in Figure 48 (p. 42) act as equal-arm lever . IN decimal scales The shoulder from which the cup with weights is suspended is 10 times longer than the shoulder carrying the load. This makes weighing large loads much easier. When weighing a load on a decimal scale, you should multiply the mass of the weights by 10.

The device of scales for weighing freight cars of cars is also based on the rule of leverage.

Levers are also found in different parts bodies of animals and humans. These are, for example, arms, legs, jaws. Many levers can be found in the body of insects (by reading a book about insects and the structure of their bodies), birds, and in the structure of plants.

Application of the law of equilibrium of a lever to a block.

Block It is a wheel with a groove, mounted in a holder. A rope, cable or chain is passed through the block groove.

Fixed block This is called a block whose axis is fixed and does not rise or fall when lifting loads (Fig.).

A fixed block can be considered as an equal-armed lever, in which the arms of forces are equal to the radius of the wheel (Fig): OA = OB = r. Such a block does not provide a gain in strength. ( F 1 = F 2), but allows you to change the direction of the force. Movable block - this is a block. the axis of which rises and falls along with the load (Fig.). The figure shows the corresponding lever: ABOUT- fulcrum point of the lever, OA- shoulder strength R And OB- shoulder strength F. Since the shoulder OB 2 times the shoulder OA, then the strength F 2 times less force R:

F = P/2 .

Thus, the movable block gives a 2-fold gain in strength .

This can be proven using the concept of moment of force. When the block is in equilibrium, the moments of forces F And R equal to each other. But the shoulder of strength F 2 times the leverage R, and, therefore, the power itself F 2 times less force R.

Usually in practice a combination of a fixed block and a movable one is used (Fig.). The fixed block is used for convenience only. It does not give a gain in force, but it changes the direction of the force. For example, it allows you to lift a load while standing on the ground. This comes in handy for many people or workers. However, it gives a gain in strength 2 times greater than usual!

Equality of work when using simple mechanisms. "Golden rule" of mechanics.

The simple mechanisms we have considered are used when performing work in cases where it is necessary to balance another force through the action of one force.

Naturally, the question arises: while giving a gain in power or path, don’t simple mechanisms give a gain in work? The answer to this question can be obtained from experience.

By balancing two different magnitude forces on a lever F 1 and F 2 (fig.), set the lever in motion. It turns out that at the same time the point of application of the smaller force F 2 goes further s 2, and the point of application of the greater force F 1 - shorter path s 1. Having measured these paths and force modules, we find that the paths traversed by the points of application of forces on the lever are inversely proportional to the forces:

s 1 / s 2 = F 2 / F 1.

Thus, acting on the long arm of the lever, we gain in strength, but at the same time we lose by the same amount along the way.

Product of force F on the way s there is work. Our experiments show that the work done by the forces applied to the lever is equal to each other:

F 1 s 1 = F 2 s 2, i.e. A 1 = A 2.

So, When using leverage, you won’t be able to win at work.

By using leverage, we can gain either power or distance. By applying force to the short arm of the lever, we gain in distance, but lose by the same amount in strength.

There is a legend that Archimedes, delighted with the discovery of the rule of leverage, exclaimed: “Give me a fulcrum and I will turn the Earth over!”

Of course, Archimedes could not cope with such a task even if he had been given a fulcrum (which should have been outside the Earth) and a lever of the required length.

To raise the earth just 1 cm, the long arm of the lever would have to describe an arc of enormous length. It would take millions of years to move the long end of the lever along this path, for example, at a speed of 1 m/s!

A stationary block does not give any gain in work, which is easy to verify experimentally (see figure). Ways, passable points application of forces F And F, are the same, the forces are the same, which means the work is the same.

You can measure and compare the work done with the help of a moving block. In order to lift a load to a height h using a movable block, it is necessary to move the end of the rope to which the dynamometer is attached, as experience shows (Fig.), to a height of 2h.

Thus, getting a 2-fold gain in strength, they lose 2-fold on the way, therefore, the movable block does not give a gain in work.

Centuries-old practice has shown that None of the mechanisms gives a gain in performance. They apply the same various mechanisms in order to win in strength or on the way, depending on the working conditions.

Already ancient scientists knew a rule applicable to all mechanisms: no matter how many times we win in strength, the same number of times we lose in distance. This rule has been called the "golden rule" of mechanics.

Efficiency of the mechanism.

When considering the design and action of the lever, we did not take into account friction, as well as the weight of the lever. in these ideal conditions work done by the applied force (we will call this work full), is equal to useful work on lifting loads or overcoming any resistance.

In practice, the total work done by a mechanism is always slightly greater than the useful work.

Part of the work is done against the frictional force in the mechanism and by moving its individual parts. So, when using a movable block, you have to additionally do work to lift the block itself, the rope and determine the friction force in the axis of the block.

Whatever mechanism we take, the useful work done with its help always constitutes only a part of the total work. This means, denoting useful work by the letter Ap, total (expended) work by the letter Az, we can write:

Up< Аз или Ап / Аз < 1.

The ratio of useful work to full time job called coefficient useful action mechanism.

The efficiency factor is abbreviated as efficiency.

Efficiency = Ap / Az.

Efficiency is usually expressed as a percentage and is denoted by the Greek letter η, read as “eta”:

η = Ap / Az · 100%.

Example: A load weighing 100 kg is suspended on the short arm of a lever. To lift it, a force of 250 N is applied to the long arm. The load is raised to a height of h1 = 0.08 m, while the point of application of the driving force drops to a height of h2 = 0.4 m. Find the efficiency of the lever.

Let's write down the conditions of the problem and solve it.

Given :

Solution :

η = Ap / Az · 100%.

Total (expended) work Az = Fh2.

Useful work Ap = Рh1

P = 9.8 100 kg ≈ 1000 N.

Ap = 1000 N · 0.08 = 80 J.

Az = 250 N · 0.4 m = 100 J.

η = 80 J/100 J 100% = 80%.

Answer : η = 80%.

But " Golden Rule"is carried out in this case as well. Part of the useful work - 20% of it - is spent on overcoming friction in the axis of the lever and air resistance, as well as on the movement of the lever itself.

The efficiency of any mechanism is always less than 100%. When designing mechanisms, people strive to increase their efficiency. To achieve this, friction in the axes of the mechanisms and their weight are reduced.

Energy.

In plants and factories, machines and machines are driven by electric motors, which consume electrical energy(hence the name).

1.5. MECHANICAL WORK AND KINETIC ENERGY

The concept of energy. Mechanical energy. Work is a quantitative measure of energy change. Work of resultant forces. Work of forces in mechanics. The concept of power. Kinetic energy as a measure of mechanical motion. Communication change ki netic energy with the work of internal and external forces.Kinetic energy of a system in various reference systems.Koenig's theorem.

Energy - it is a universal measure of various forms of movement and interaction. M mechanical energy describes the amount potentialAndkinetic energy, available in the components mechanical system . Mechanical energy- this is the energy associated with the movement of an object or its position, the ability to perform mechanical work.

Work of force - this is a quantitative characteristic of the process of energy exchange between interacting bodies.

Let a particle, under the influence of a force, move along a certain trajectory 1-2 (Fig. 5.1). In general, the force in the process

The movement of a particle can change both in magnitude and in direction. Let us consider, as shown in Fig. 5.1, an elementary displacement within which the force can be considered constant.

The effect of force on displacement is characterized by a value equal to the scalar product, which is called basic work moving forces. It can be presented in another form:

,

where is the angle between the vectors and is the elementary path, the projection of the vector onto the vector is indicated (Fig. 5.1).

So, the elementary work of force on displacement

The quantity is algebraic: depending on the angle between the force vectors and or on the sign of the projection of the force vector onto the displacement vector, it can be either positive or negative and, in particular, equal to zero if i.e. . The SI unit of work is the Joule, abbreviated J.

By summing (integrating) expression (5.1) over all elementary sections of the path from point 1 to point 2, we find the work done by the force on a given displacement:

it is clear that the elementary work A is numerically equal to the area of ​​the shaded strip, and the work A on the path from point 1 to point 2 is the area of ​​the figure bounded by the curve, ordinates 1 and 2 and the s axis. In this case, the area of ​​the figure above the s-axis is taken with a plus sign (it corresponds to positive work), and the area of ​​the figure under the s-axis is taken with a minus sign (it corresponds to negative work).

Let's look at examples of how to calculate work. Work of elastic force where is the radius vector of particle A relative to point O (Fig. 5.3).

Let us move particle A, which is acted upon by this force, along an arbitrary path from point 1 to point 2. Let us first find the elementary work of force on elementary displacement:

.

Scalar product where is the projection of the displacement vector onto the vector . This projection is equal to the increment of the modulus of the vector. Therefore,

Now let’s calculate the work done by this force along the entire path, i.e., integrate the last expression from point 1 to point 2:

Let's calculate the work of the gravitational (or mathematically analogous Coulomb force) force. Let there be a stationary point mass (point charge) at the beginning of the vector (Fig. 5.3). Let us determine the work done by the gravitational (Coulomb) force when particle A moves from point 1 to point 2 along an arbitrary path. The force acting on particle A can be represented as follows:

where the parameter for the gravitational interaction is equal to , and for the Coulomb interaction its value is equal to . Let us first calculate the elementary work of this force on displacement

As in the previous case, the scalar product is therefore

.

The work of this force all the way from point 1 to point 2

Let us now consider the work of a uniform force of gravity. Let us write this force in the form where unit vertical axis z with a positive direction is indicated (Fig. 5.4). Elementary work of gravity on displacement

Scalar product where the projection onto the unit unit is equal to the increment of the z coordinate. Therefore, the expression for work takes the form

The work done by a given force all the way from point 1 to point 2

The forces considered are interesting in the sense that their work, as can be seen from formulas (5.3) - (5.5), does not depend on the shape of the path between points 1 and 2, but depends only on the position of these points. This very important feature of these forces is not inherent, however, to all forces. For example, the friction force does not have this property: the work of this force depends not only on the position of the starting and ending points, but also on the shape of the path between them.

Until now we have been talking about the work of one force. If several forces act on a particle in the process of motion, the resultant of which is then it is easy to show that the work of the resulting force on a certain displacement is equal to the algebraic sum of the work performed by each of the forces separately on the same displacement. Really,

Let us introduce a new quantity into consideration - power. It is used to characterize the speed at which work is done. Power , a-priory, - is the work done by a force per unit time . If a force does work over a period of time, then the power developed by this force at a given moment in time is Considering that , we get

The SI unit of power is the watt, abbreviated as W.

Thus, the power developed by force is equal to the scalar product of the force vector and the speed vector with which the point of application of this force moves. Like work, power is an algebraic quantity.

Knowing the power of the force, we can also find the work done by this force over a period of time t. Indeed, presenting the integrand in (5.2) as we get

You should also pay attention to one very significant circumstance. When talking about work (or power), it is necessary in each specific case to clearly indicate or imagine the work what kind of strength(or forces) is meant. Otherwise, as a rule, misunderstandings are inevitable.

Let's consider the concept particle kinetic energy. Let a particle of mass T moves under the influence of some force (in the general case, this force can be the result of several forces). Let's find the elementary work that this force does on an elementary displacement. Keeping in mind that and , we write

.

Scalar product where is the projection of the vector onto the direction of the vector. This projection is equal to the increment of the magnitude of the velocity vector. Therefore, the elementary work

From this it is clear that the work of the resulting force goes to increase a certain value in parentheses, which is called kinetic energy particles.

and upon final movement from point 1 to point 2

i.e. the increment in the kinetic energy of a particle at a certain displacement is equal to the algebraic sum of the work of all forces, acting on the particle at the same displacement. If then, that is, the kinetic energy of the particle increases; if that is, then the kinetic energy decreases.

Equation (5.9) can be presented in another form by dividing both sides by the corresponding time interval dt:

This means that the time derivative of the kinetic energy of a particle is equal to the power N of the resulting force acting on the particle.

Now let's introduce the concept kinetic energy of the system . Let us consider an arbitrary system of particles in a certain reference frame. Let a particle of the system have kinetic energy at a given moment. The increment in the kinetic energy of each particle is equal, according to (5.9), to the work of all forces acting on this particle: Let us find the elementary work performed by all forces acting on all particles of the system:

where is the total kinetic energy of the system. Note that the kinetic energy of the system is the quantity additive : it is equal to the sum of the kinetic energies of the individual parts of the system, regardless of whether they interact with each other or not.

So, the increase in the kinetic energy of the system is equal to the work done by all the forces acting on all particles of the system. With the elementary movement of all particles

and at the final movement

i.e. the time derivative of the kinetic energy of the system is equal to the total power of all forces acting on all particles of the system,

Koenig's theorem: kinetic energy K systems of particles can be represented as the sum of two terms: a) kinetic energy mV c 2 /2 an imaginary material point whose mass is equal to the mass of the entire system, and whose speed coincides with the speed of the center of mass; b) kinetic energy K rel system of particles calculated in the center of mass system.