Finding the roots of a quadratic trinomial

Goals: introduce the concept of a quadratic trinomial and its roots; develop the ability to find the roots of a quadratic trinomial.

During the classes

I. Organizational moment.

II. Oral work.

Which of the numbers: –2; -1; 1; 2 – are the roots of the equations?

a) 8 X+ 16 = 0; V) X 2 + 3X – 4 = 0;

b) 5 X 2 – 5 = 0; G) X 3 – 3X – 2 = 0.

III. Explanation of new material.

Explanation of new material should be carried out according to the following scheme:

1) Introduce the concept of the root of a polynomial.

2) Introduce the concept of a quadratic trinomial and its roots.

3) Analyze the question of the possible number of roots of a square trinomial.

The question of isolating the square of a binomial from a square trinomial is best discussed in the next lesson.

At each stage of explaining new material, it is necessary to offer students an oral task to test their mastery of the main points of the theory.

Task 1. Which of the numbers: –1; 1; ; 0 – are the roots of the polynomial X 4 + 2X 2 – 3?

Assignment 2. Which of the following polynomials are quadratic trinomials?

1) 2X 2 + 5X – 1; 6) X 2 – X – ;

2) 2X – ; 7) 3 – 4X + X 2 ;

3) 4X 2 + 2X + X 3 ; 8) X + 4X 2 ;

4) 3X 2 – ; 9) + 3X – 6;

5) 5X 2 – 3X; 10) 7X 2 .

Which quadratic trinomials have root 0?

Task 3. Can a square trinomial have three roots? Why? How many roots does a square trinomial have? X 2 + X – 5?

IV. Formation of skills and abilities.

Exercises:

1. № 55, № 56, № 58.

2. No. 59 (a, c, d), No. 60 (a, c).

In this task you do not need to look for the roots of quadratic trinomials. It is enough to find their discriminant and answer the question posed.

a) 5 X 2 – 8X + 3 = 0;

D 1 = 16 – 15 = 1;

D 1 0, which means that this quadratic trinomial has two roots.

b) 9 X 2 + 6X + 1 = 0;

D 1 = 9 – 9 = 0;

D 1 = 0, which means the square trinomial has one root.

at 7 X 2 + 6X – 2 = 0;

7X 2 – 6X + 2 = 0;

D 1 = 9 – 14 = –5;

If there is time left, you can do No. 63.

Solution

Let ax 2 + bx + c is a given quadratic trinomial. Because the a+ b +
+c= 0, then one of the roots of this trinomial is equal to 1. By Vieta’s theorem, the second root is equal to . According to the condition, With = 4A, so the second root of this quadratic trinomial is equal to
.

ANSWER: 1 and 4.

V. Lesson summary.

Frequently asked questions:

– What is the root of a polynomial?

– Which polynomial is called a quadratic trinomial?

– How to find the roots of a quadratic trinomial?

– What is the discriminant of a quadratic trinomial?

– How many roots can a square trinomial have? What does this depend on?

Homework: No. 57, No. 59 (b, d, f), No. 60 (b, d), No. 62.

Teacher of the highest category: Minaichenko N.S., gymnasium No. 24, Sevastopol

Lesson in 8th grade: "Square trinomial and its roots"

Lesson type : lesson of new knowledge.

The purpose of the lesson:

organize student activities to consolidate and develop knowledge about the decomposition of a quadratic trinomial into linear factors and the reduction of fractions;

develop skills in applying knowledge of all methods of factorization: bracketing, using abbreviated multiplication formulas and grouping methods in order to prepare for successful completion algebra exam;

create conditions for development cognitive interest to the subject, formation logical thinking and self-control when using factorization.

Equipment: multimedia projector, screen, presentation: “Roots of the square trinomial”, crossword puzzle, test, handouts.

Basic Concepts . Decomposition quadratic trinomial by multipliers.

Independent activity of students. Application of the theorem on the factorization of a quadratic trinomial in solving problems.

Lesson Plan

Problem solving.

Answers to student questions

IV. Primary test of knowledge acquisition. Reflection

Teacher's message.

Student message

V. Homework

Writing on the board

Methodological comment:

This topic is fundamental in the section “Identity transformations” algebraic expressions" Therefore, it is important that students automatically be able not only to see factorization formulas in examples, but also to apply them in other tasks: such as solving equations, transforming expressions, proving identities.

This topic focuses on factoring a quadratic trinomial:

ax+ bx + c = a(x – x)(x – x),

where x and x – roots quadratic equation ax + bx + c = 0.

This allows you to expand the student’s field of vision, teach him to think in non-standard situation, using the material being studied, i.e. using the formula for factoring a quadratic trinomial:

ability to reduce algebraic fractions;

ability to simplify algebraic expressions;

ability to solve equations;

ability to prove identities.

Main lesson content:

a) 3x + 5x – 2;

b) –x + 16x – 15;

c) x – 12x + 24;

d) –5x + 6x – 1.

№2. Reduce the fraction:

№3. Simplify the expression:

№4. Solve the equation:

b)

During the classes:

I. Stage of updating knowledge.

Motivation for learning activities.

a) from history:

b) crossword:

Warm-up-train the mind – crossword puzzle:

Horizontally:

1) The root of the second degree is called…. (square)

2) Values ​​of the variable at which the equation becomes a true equality (roots)

3) An equality containing an unknown is called... (equation)

4) Indian scientist, which outlined general rule solving quadratic equations (Brahmagupta)

5) The coefficients of the quadratic equation are... (numbers)

6) Ancient Greek scientist who invented a geometric method for solving equations (Euclid)

7) Theorem relating coefficients and roots of a quadratic equation (Vieta)

8) “discriminant”, determining the roots of a quadratic equation – this is... (discriminant)

Additionally:

If D>0, how many roots? (two)

If D=0, how many roots? (one)

If D<0, сколько корней? (нет действительных корней)

Horizontal and vertical lesson topic: “Square trinomial”

b) motivation:

This topic is fundamental in the section “Identical transformations of algebraic expressions.” Therefore, it is important that you automatically be able not only to see factorization formulas in examples, but also to apply them in other tasks: such as reducing fractions, solving equations, transforming expressions, proving identities.

Today we will focus on factoring the quadratic trinomial:

II. Learning new material.

Topic: Square trinomial and its roots.

The general theory of polynomials of many variables goes far beyond the scope of the school course. Therefore, we will limit ourselves to studying polynomials of one real variable, and only in the simplest cases. Let us consider polynomials of one variable, reduced to standard form.

Root of a polynomial is the value of a variable at which the value of the polynomial is equal to zero. This means that to find the roots of a polynomial, you need to equate it to zero, i.e. solve the equation.

Root of a polynomial of the first degree
easy to find
. Examination:
.

The roots of a quadratic trinomial can be found by solving the equation:
.

Using the formula for the roots of a quadratic equation we find:

;

Theorem (on factoring a quadratic trinomial ):

If And -roots of a square trinomial
, Where ≠ 0,

That .

Proof:

Let us perform the following transformations of the quadratic trinomial:

=
=
=

=
=
=

=
=

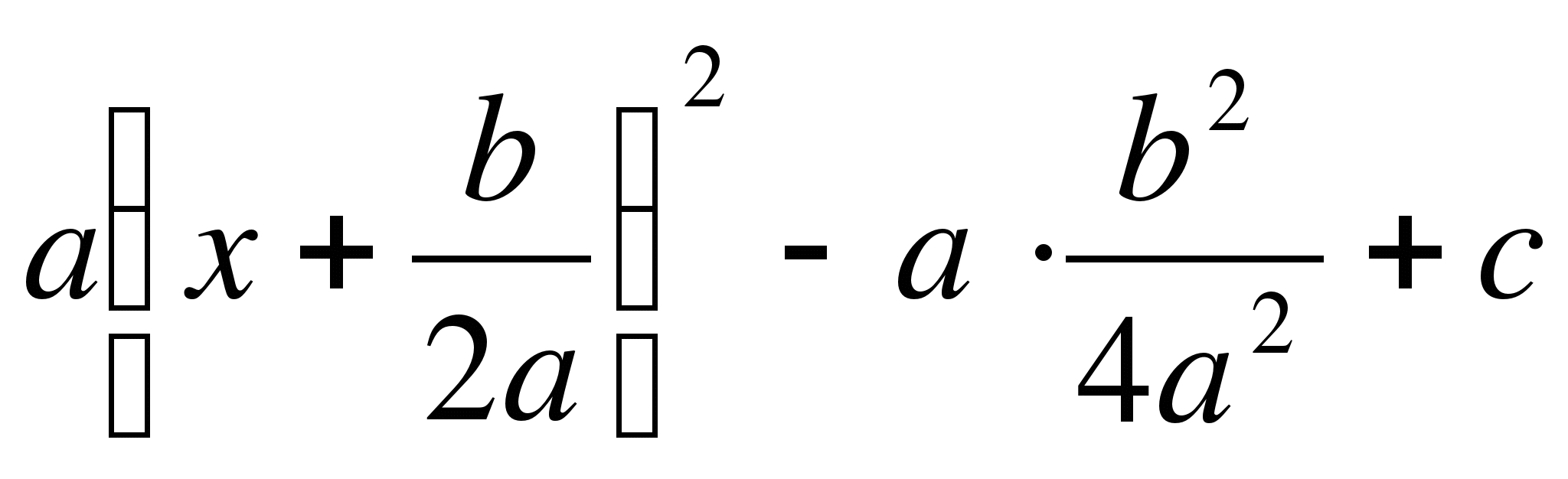Since the discriminant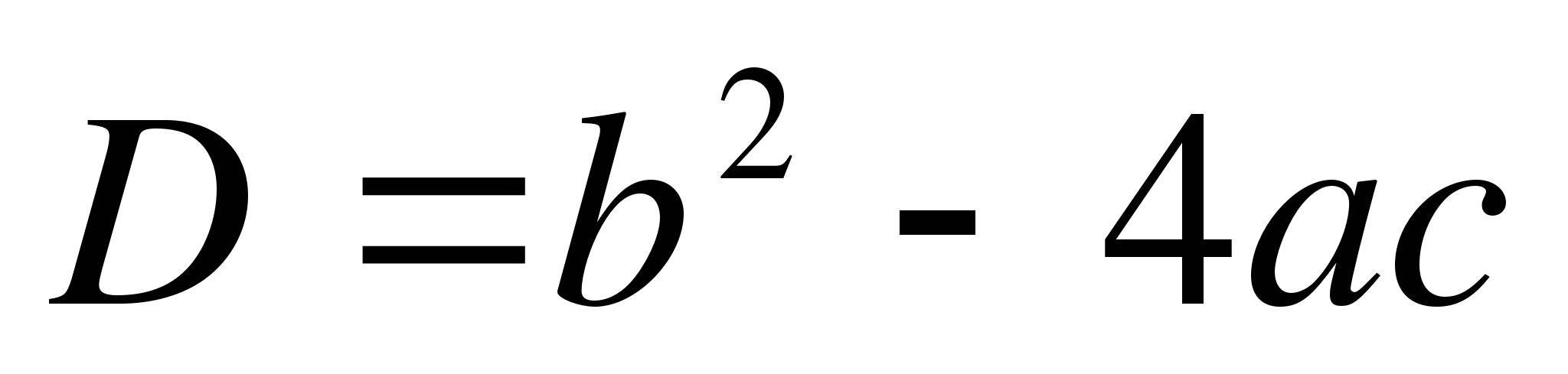
, we get:

=
=

Let us apply the difference of squares formula in brackets and get:

=
=
,

because
;
. The theorem is proven.

The resulting formula is called the formulafactoring a quadratic trinomial.

III. Formation of skills and abilities.

№1. Factor the quadratic trinomial:

a) 3x + 5x – 2;

Solution:

Answer: 3x+5x–2=3(x+2)(x-)=(x+2)(3x-1)

On the desk:

b) –5x + 6x – 1;

Additionally:

c) x – 12x + 24;

d) –x + 16x – 15.

№2. Reduce the fraction:

A)

№4. Solve the equation:

b)

IV. Primary test of knowledge acquisition.

A) Test.

Option 1.

1. Find the roots of the quadratic trinomial:2x 2 -9x-5

Answer:

2. Which polynomial must be substituted for the ellipsis in order for the equality to be true:

b) Mutual verification of options (answers and evaluation parameters are illustrated).

c) Reflection.

V. Homework.

You can find the root of a square trinomial using the discriminant. In addition, for the reduced polynomial of the second degree, Vieta’s theorem, based on the ratio of the coefficients, applies.

Instructions

• Quadratic equations are a fairly extensive topic in school algebra. The left side of such an equation is a polynomial of the second degree of the form A x² + B x + C, i.e. an expression of three monomials of varying degrees of unknown x. To find the root of a square trinomial, you need to calculate the value of x at which this expression is equal to zero.
• To solve a quadratic equation, you need to find the discriminant. Its formula is a consequence of isolating the complete square of the polynomial and represents a certain ratio of its coefficients: D = B² – 4 A C.
• The discriminant can take on various values, including being negative. And if younger schoolchildren can say with relief that such an equation has no roots, then high school students are already able to determine them based on the theory of complex numbers. So, there can be three options: Discriminant – a positive number. Then the roots of the equation are equal: x1 = (-B + √D)/2 A; x2 = (-B - √D)/2 A;
  The discriminant went to zero. Theoretically, in this case the equation also has two roots, but practically they are the same: x1 = x2 = -B/2 A;
  The discriminant is less than zero. A certain value i² = -1 is introduced into the calculation, which allows us to write a complex solution: x1 = (-B + i √|D|)/2 A; x2 = (-B - i √|D|)/2 A.
• The discriminant method is valid for any quadratic equation, but there are situations when it is advisable to use a faster method, especially for small integer coefficients. This method is called Vieta's theorem and consists of a pair of relationships between the coefficients in the reduced trinomial: x² + P x + Q
  x1 + x2 = -P;
  x1 x2 = Q. All that remains is to find the roots.
• It should be noted that the equation can be reduced to a similar form. To do this, you need to divide all the terms of the trinomial by the coefficient of the highest power A: A x² + B x + C |A
  x² + B/A x + C/A
  x1 + x2 = -B/A;
  x1 x2 = C/A.

Online calculator.
Isolating the square of a binomial and factoring a square trinomial.

This math program distinguishes the square binomial from the square trinomial, i.e. does a transformation like:
\(ax^2+bx+c \rightarrow a(x+p)^2+q \) and factorizes a quadratic trinomial: \(ax^2+bx+c \rightarrow a(x+n)(x+m) \)

Those. the problems boil down to finding the numbers \(p, q\) and \(n, m\)

The program not only gives the answer to the problem, but also displays the solution process.

This program can be useful for high school students in general education schools when preparing for tests and exams, when testing knowledge before the Unified State Exam, and for parents to control the solution of many problems in mathematics and algebra.

Or maybe it’s too expensive for you to hire a tutor or buy new textbooks? Or do you just want to get your math or algebra homework done as quickly as possible? In this case, you can also use our programs with detailed solutions.

In this way, you can conduct your own training and/or training of your younger brothers or sisters, while the level of education in the field of solving problems increases.

If you are not familiar with the rules for entering a quadratic trinomial, we recommend that you familiarize yourself with them.

Rules for entering a quadratic polynomial
Any Latin letter can act as a variable.

For example: \(x, y, z, a, b, c, o, p, q\), etc.
Numbers can be entered as whole or fractional numbers.

Moreover, fractional numbers can be entered not only in the form of a decimal, but also in the form of an ordinary fraction.
Rules for entering decimal fractions.
In decimal fractions, the fractional part can be separated from the whole part by either a period or a comma.

For example, you can enter decimal fractions like this: 2.5x - 3.5x^2
Rules for entering ordinary fractions.

Only a whole number can act as the numerator, denominator and integer part of a fraction.

The denominator cannot be negative. /
When entering a numerical fraction, the numerator is separated from the denominator by a division sign: &
The whole part is separated from the fraction by the ampersand sign:
Input: 3&1/3 - 5&6/5x +1/7x^2

Result: \(3\frac(1)(3) - 5\frac(6)(5) x + \frac(1)(7)x^2\) When entering an expression you can use parentheses
. In this case, when solving, the introduced expression is first simplified.

For example: 1/2(x-1)(x+1)-(5x-10&1/2)

Example of a detailed solution Isolating the square of a binomial. Answer:$$2x^2+2x-4 = 2\left(x+\frac(1)(2) \right)^2-\frac(9)(2) $$ Factorization.$$ ax^2+bx+c \rightarrow a(x+n)(x+m) $$ $$2x^2+2x-4 = $$
$$ 2\left(x^2+x-2 \right) = $$
$$ 2 \left(x^2+2x-1x-1 \cdot 2 \right) = $$ $$ 2 \left(x \left(x +2 \right) -1 \left(x +2 \right ) \right) = $$ $$ 2 \left(x -1 \right) \left(x +2 \right) $$ Answer:$$2x^2+2x-4 = 2 \left(x -1 \right) \left(x +2 \right) $$

Decide

It was discovered that some scripts necessary to solve this problem were not loaded, and the program may not work.
You may have AdBlock enabled.
In this case, disable it and refresh the page.

JavaScript is disabled in your browser.
For the solution to appear, you need to enable JavaScript.
Here are instructions on how to enable JavaScript in your browser.

Because There are a lot of people willing to solve the problem, your request has been queued.
In a few seconds the solution will appear below.
Please wait sec...

If you noticed an error in the solution, then you can write about this in the Feedback Form.
Do not forget indicate which task you decide what enter in the fields.

Our games, puzzles, emulators:

A little theory.

Isolating the square of a binomial from a square trinomial

If the square trinomial ax 2 +bx+c is represented as a(x+p) 2 +q, where p and q are real numbers, then we say that from square trinomial, the square of the binomial is highlighted.

From the trinomial 2x 2 +12x+14 we extract the square of the binomial.

\(2x^2+12x+14 = 2(x^2+6x+7) \)

To do this, imagine 6x as a product of 2*3*x, and then add and subtract 3 2. We get:
$$ 2(x^2+2 \cdot 3 \cdot x + 3^2-3^2+7) = 2((x+3)^2-3^2+7) = $$ $$ = 2 ((x+3)^2-2) = 2(x+3)^2-4 $$

That. We extract the square binomial from the square trinomial, and showed that:
$$ 2x^2+12x+14 = 2(x+3)^2-4 $$

Factoring a quadratic trinomial

If the square trinomial ax 2 +bx+c is represented in the form a(x+n)(x+m), where n and m are real numbers, then the operation is said to have been performed factorization of a quadratic trinomial.

Let us show with an example how this transformation is done.

Let's factor the quadratic trinomial 2x 2 +4x-6.

Let us take the coefficient a out of brackets, i.e. 2:
\(2x^2+4x-6 = 2(x^2+2x-3) \)

Let's transform the expression in brackets.
To do this, imagine 2x as the difference 3x-1x, and -3 as -1*3. We get:
$$ = 2(x^2+3 \cdot x -1 \cdot x -1 \cdot 3) = 2(x(x+3)-1 \cdot (x+3)) = $$
$$ = 2(x-1)(x+3) $$

That. We factored the quadratic trinomial, and showed that:
$$ 2x^2+4x-6 = 2(x-1)(x+3) $$

Note that factoring a quadratic trinomial is possible only if the quadratic equation corresponding to this trinomial has roots.
Those. in our case, it is possible to factor the trinomial 2x 2 +4x-6 if the quadratic equation 2x 2 +4x-6 =0 has roots. In the process of factorization, we established that the equation 2x 2 + 4x-6 = 0 has two roots 1 and -3, because with these values, the equation 2(x-1)(x+3)=0 turns into a true equality.

Books (textbooks) Abstracts of the Unified State Examination and the Unified State Examination tests online Games, puzzles Plotting graphs of functions Spelling dictionary of the Russian language Dictionary of youth slang Catalog of Russian schools Catalog of secondary educational institutions of Russia Catalog of Russian universities List of tasks

Expanding polynomials to obtain a product can sometimes seem confusing. But it's not that difficult if you understand the process step by step. The article describes in detail how to factor a quadratic trinomial.

Many people do not understand how to factor a square trinomial, and why this is done. At first it may seem like a futile exercise. But in mathematics nothing is done for nothing. The transformation is necessary to simplify the expression and ease of calculation.

A polynomial of the form – ax²+bx+c, called a quadratic trinomial. The term "a" must be negative or positive. In practice, this expression is called a quadratic equation. Therefore, sometimes they say it differently: how to expand a quadratic equation.

Interesting! A polynomial is called a square because of its largest degree, the square. And a trinomial - because of the 3 components.

Some other types of polynomials:

• linear binomial (6x+8);
• cubic quadrinomial (x³+4x²-2x+9).

Factoring a quadratic trinomial

First, the expression is equal to zero, then you need to find the values ​​of the roots x1 and x2. There may be no roots, there may be one or two roots. The presence of roots is determined by the discriminant. You need to know its formula by heart: D=b²-4ac.

If the result D is negative, there are no roots. If positive, there are two roots. If the result is zero, the root is one. The roots are also calculated using the formula.

If, when calculating the discriminant, the result is zero, you can use any of the formulas. In practice, the formula is simply shortened: -b / 2a.

The formulas for different discriminant values ​​are different.

If D is positive:

If D is zero:

Online calculators

There is an online calculator on the Internet. It can be used to perform factorization. Some resources provide the opportunity to view the solution step by step. Such services help to better understand the topic, but you need to try to understand it well.

Useful video: Factoring a quadratic trinomial

Examples

We suggest looking at simple examples of how to factor a quadratic equation.

Example 1

This clearly shows that the result is two x's because D is positive. They need to be substituted into the formula. If the roots turn out to be negative, the sign in the formula changes to the opposite.

We know the formula for factoring a quadratic trinomial: a(x-x1)(x-x2). We put the values ​​in brackets: (x+3)(x+2/3). There is no number before a term in a power. This means that there is one there, it goes down.

Example 2

This example clearly shows how to solve an equation that has one root.

We substitute the resulting value:

Example 3

Given: 5x²+3x+7

First, let's calculate the discriminant, as in previous cases.

D=9-4*5*7=9-140= -131.

The discriminant is negative, which means there are no roots.

After receiving the result, you should open the brackets and check the result. The original trinomial should appear.

Alternative solution

Some people were never able to make friends with the discriminator. There is another way to factorize a quadratic trinomial. For convenience, the method is shown with an example.

Given: x²+3x-10

We know that we should get 2 brackets: (_)(_). When the expression looks like this: x²+bx+c, at the beginning of each bracket we put x: (x_)(x_). The remaining two numbers are the product that gives "c", i.e. in this case -10. The only way to find out what numbers these are is by selection. The substituted numbers must correspond to the remaining term.

For example, multiplying the following numbers gives -10:

• -1, 10;
• -10, 1;
• -5, 2;
• -2, 5.

1. (x-1)(x+10) = x2+10x-x-10 = x2+9x-10. No.
2. (x-10)(x+1) = x2+x-10x-10 = x2-9x-10. No.
3. (x-5)(x+2) = x2+2x-5x-10 = x2-3x-10. No.
4. (x-2)(x+5) = x2+5x-2x-10 = x2+3x-10. Fits.

This means that the transformation of the expression x2+3x-10 looks like this: (x-2)(x+5).

Important! You should be careful not to confuse the signs.

Expansion of a complex trinomial

If “a” is greater than one, difficulties begin. But everything is not as difficult as it seems.

To factorize, you first need to see if anything can be factored out.

For example, given the expression: 3x²+9x-30. Here the number 3 is taken out of brackets:

3(x²+3x-10). The result is the already well-known trinomial. The answer looks like this: 3(x-2)(x+5)

How to decompose if the term that is in the square is negative? In this case, the number -1 is taken out of brackets. For example: -x²-10x-8. The expression will then look like this:

The scheme differs little from the previous one. There are just a few new things. Let's say the expression is given: 2x²+7x+3. The answer is also written in 2 brackets that need to be filled in (_)(_). In the 2nd bracket is written x, and in the 1st what is left. It looks like this: (2x_)(x_). Otherwise, the previous scheme is repeated.

The number 3 is given by the numbers:

• -1, -3;
• -3, -1;
• 3, 1;
• 1, 3.

We solve equations by substituting these numbers. The last option is suitable. This means that the transformation of the expression 2x²+7x+3 looks like this: (2x+1)(x+3).

Other cases

It is not always possible to convert an expression. With the second method, solving the equation is not required. But the possibility of transforming terms into a product is checked only through the discriminant.

It is worth practicing solving quadratic equations so that when using the formulas there are no difficulties.

Useful video: factoring a trinomial

Conclusion

You can use it in any way. But it’s better to practice both until they become automatic. Also, learning how to solve quadratic equations well and factor polynomials is necessary for those who are planning to connect their lives with mathematics. All the following mathematical topics are built on this.