Coordinate method for finding the angle between straight lines. Method of coordinates in space: formulas and tutor comments

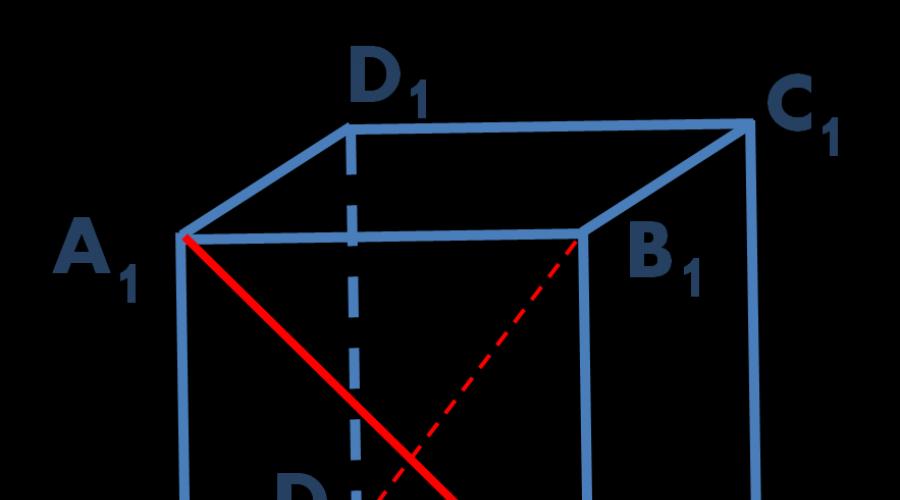
In this article, using the example of solving problem C2 from the Unified State Examination, the method of finding using the coordinate method is analyzed. Recall that straight lines are skew if they do not lie in the same plane. In particular, if one line lies in a plane, and the second line intersects this plane at a point that does not lie on the first line, then such lines are intersecting (see figure).

To find distances between crossing lines necessary:

1. Draw a plane through one of the intersecting lines that is parallel to the other intersecting line.
2. Drop a perpendicular from any point of the second line onto the resulting plane. The length of this perpendicular will be the required distance between the lines.

Let us analyze this algorithm in more detail using the example of solving problem C2 from the Unified State Examination in mathematics.

Distance between lines in space

Task. In a unit cube ABCDA 1 B 1 C 1 D 1 find the distance between the lines B.A. 1 and D.B. 1 .

Rice. 1. Drawing for the task

Solution. Through the middle of the diagonal of the cube D.B. 1 (point O) draw a line parallel to the line A 1 B. Points of intersection of this line with edges B.C. And A 1 D 1 is denoted accordingly N And M. Straight MN lies in a plane MNB 1 and parallel to the line A 1 B, which does not lie in this plane. This means that the straight line A 1 B parallel to the plane MNB 1 based on the parallelism of a straight line and a plane (Fig. 2).

Rice. 2. The required distance between intersecting lines is equal to the distance from any point of the selected line to the depicted plane

Now we are looking for the distance from some point on the line A 1 B to plane MNB 1 . This distance, by definition, will be the required distance between the crossing lines.

To find this distance we will use the coordinate method. Let us introduce a rectangular Cartesian coordinate system so that its origin coincides with point B, axis X was directed along the edge B.A., axis Y- along the rib B.C., axis Z- along the rib BB 1 (Fig. 3).

Rice. 3. We choose a rectangular Cartesian coordinate system as shown in the figure

Finding the equation of the plane MNB 1 in this coordinate system. To do this, we first determine the coordinates of the points M, N And B 1: We substitute the resulting coordinates into the general equation of the straight line and obtain the following system of equations:

From the second equation of the system we obtain from the third we obtain after which from the first we obtain Substitute the obtained values ​​into the general equation of the straight line:

We note that otherwise the plane MNB 1 would pass through the origin. Divide both sides of this equation by and we get:

The distance from a point to a plane is determined by the formula.

Using the coordinate method when calculating an angle

between planes

Most general method finding the anglebetween planes - the coordinate method (sometimes using vectors). It can be used when all others have been tried. But there are situations in which the coordinate method makes sense to apply immediately, namely when the coordinate system is naturally related to the polyhedron specified in the problem statement, i.e. Three pairwise perpendicular lines are clearly visible, on which coordinate axes can be specified. Such polyhedra are cuboid and a regular quadrangular pyramid. In the first case, the coordinate system can be specified by edges extending from one vertex (Fig. 1), in the second - by the height and diagonals of the base (Fig. 2)

The application of the coordinate method is as follows.

A rectangular coordinate system in space is introduced. It is advisable to introduce it in a “natural” way - to “link” it to a trio of pairwise perpendicular lines that have a common point.

For each of the planes, the angle between which is sought, an equation is drawn up. The easiest way to create such an equation is to know the coordinates of three points on the plane that do not lie on the same line.

Equation of the plane in general view looks like Ax + By + Cz + D = 0.

Coefficients A, B, The Cs in this equation are the coordinates of the normal vector of the plane (the vector perpendicular to the plane). We then determine the lengths and scalar product of normal vectors to the planes, the angle between which is sought. If the coordinates of these vectors(A 1, B 1; C 1) and (A 2; B 2; C 2 ), then the desired anglecalculated by the formula

Comment. It must be remembered that the angle between vectors (as opposed to the angle between planes) can be obtuse, and in order to avoid possible uncertainty, the numerator on the right side of the formula contains a modulus.

Solve this problem using the coordinate method.

Problem 1. Given a cube ABCDA 1 B 1 C 1 D 1 . Point K is the middle of edge AD, point L is the middle of edge CD. What is the angle between planes A? 1 KL and A 1 AD?

Solution . Let the origin of the coordinate system be at the point A, and the coordinate axes go along the rays AD, AB, AA 1 (Fig. 3). Let’s take the edge of the cube to be equal to 2 (it’s convenient to divide it in half). Then the coordinates of the points A 1 , K, L are as follows: A 1 (0; 0; 2), K(1; 0; 0), L(2; 1; 0).

Rice. 3

Let us write down the equation of the plane A 1 K L in general. Then we substitute the coordinates of the selected points of this plane into it. We obtain a system of three equations with four unknowns:

Let's express the coefficients A, B, C through D and we arrive at the equation

Dividing both parts into D (why D = 0?) and then multiplying by -2, we get the equation of the plane A 1 KL: 2x - 2 y + z - 2 = 0. Then the normal vector to this plane has coordinates (2: -2; 1). Plane equation A 1 AD is: y=0, and the coordinates of the normal vector to it are, for example, (0; 2: 0). According to the above formula for the cosine of the angle between planes, we obtain:

In assignment C2 in mathematics, you most often need to solve a problem in which you need to determine:

1. Distance between two points
2. Distance from point to line
3. Distance from point to plane
4. Distance between crossing lines
5. Angle between two straight lines
6. Angle between a straight line and a plane
7. Angle between planes

The tasks are elementary if you follow the solution algorithm C2 and remember the basics trigonometric properties, such as the properties of diagonals or the surface area of ​​a polyhedron. Basic tasks will help you remember these basic properties.

Now let's move directly to the algorithms.

1. To determine the distance between two points A and B, we use one of two methods:

• We include AB in some triangle and find its length as the side of the triangle
• According to the formula

Moreover, the coordinate method, in my opinion, is the simplest; you just need to carefully determine the coordinates of each point.

2. To determine the distance from a point to a line, calculate

• as the length of a perpendicular segment, if it is possible to include this segment in some triangle as one of the heights

using the coordinate method using formulas for calculating area, in which the required distance will be height and

3. The distance from a point to a plane is

• the length of the perpendicular dropped from this point onto the plane. To do this, we carefully construct a section that is perpendicular to the plane and passes through given point. The required distance will be equal to the height of the resulting new polyhedron.
• Using the coordinate method

The equation is found by substituting the coordinates of three points belonging to this plane

• Using the vector method

To do this, you need to remember the rules for adding and subtracting vectors, that the product of perpendicular vectors is equal to zero.

• Using the volume method, if there is a pyramid ABCM, then the distance from point M to the plane containing the triangle ABC is calculated by the formula

• Using the method of reference problems, which can be viewed

4. The distance between crossing lines can be solved using

4.1. Step-by-step computational method:

• construct a common perpendicular of two intersecting lines and find its length;
• construct a plane containing one of the lines and parallel to the second. Then the required distance will be equal to the distance from the point to the straight line constructed in the plane;
• enclose the data directly in parallel planes, passing through these intersecting lines, find the distance between these planes
• construct a plane perpendicular to one of these lines and construct an orthogonal projection of the second line

4.2. Vector coordinate method

• Find the coordinates of the ends of a segment that is a common perpendicular to two intersecting lines
• Finding the distance between two points

4.3. Vector method
We reduce the problem to determining the length of a vector belonging to a perpendicular that is the common perpendicular of two skew lines

6. Angle between a straight line and a plane determined by including it in right triangle as one of sharp corners, or by the vector-coordination method

We'll look at how the angle between planes is determined in the next lesson. These algorithms for solving C2 contribute to a comprehensive understanding of the method for solving the problem. "A magazine for schoolchildren and their parents to help schoolchildren." Read more: http://education-club.ru/#ixzz2IXf5GOJU

7. Angle between planes(geometric method)

• 1. Find the straight line along which the planes intersect.
• 2. Select a point on this line and draw two perpendiculars to it, lying in these planes. Or draw a plane perpendicular to the line of intersection of the planes.
• 3. Find the trigonometric function of the angle formed by perpendiculars to the line of intersection of the planes. As a rule, we do this through a triangle that includes the desired angle.
• 4. Write down the value of the angle in your answer, or trigonometric function corner.

Angle between planes. Coordinate method. Task C2

Two intersecting planes form two pairs of equal dihedral angles:

The magnitude of the dihedral angle is measured by the magnitude of the corresponding linear angle.

To construct a linear angle of a dihedral angle, you need to take an arbitrary point on the line of intersection of the planes, and in each plane draw a ray to this point perpendicular to the line of intersection of the planes. The angle formed by these rays is the linear angle of the dihedral angle:

The magnitude of the angle between planes is the magnitude of the less than dihedral angle.

Let our planes be defined by the equations:

The cosine of the angle between the planes is found by the following formula:

In the answer we write , since the value of the angle between the planes is the value of the smaller dihedral angle.

In the right quadrangular prism with a base side of 12 and a height of 21, a point M is taken on the edge so that . Point K is taken on the edge so that . Find the angle between the plane and the plane.

Let's make a drawing. Since we will use the coordinate method, we will immediately introduce a coordinate system: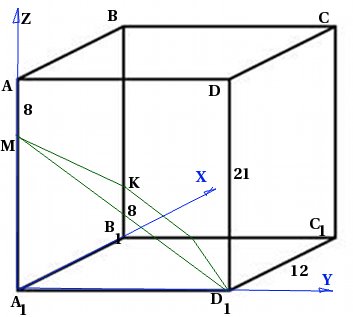

Now we are faced with the task of writing the equations of plane and plane.

I described a detailed algorithm for finding the equation of a plane using three points.

After we find the coefficients in the plane and plane equations, we substitute them into the formula to find the cosine of the angle between the planes, and find the angle.

I suggest you watch a detailed video solution to this problem:

Another task from Inna Vladimirovna Feldman

Video lessons "Coordinate method for solving problems s-2"

Lesson 2 http://youtu.be/dKQWG8OZRGo
Lesson 3 http://youtu.be/ddgr0PnbFno
Lesson 4 http://youtu.be/n6yx2pQC0Lo
Lesson 5 http://youtu.be/JkWbxAw1YLI
Lesson 6 http://youtu.be/gybIqCMKBiI
lesson 7 http://youtu.be/_LpARpYxp5g
lesson 8 http://youtu.be/XJhyZQoofD8

The coordinate method is very effective and universal method finding any angles or distances between stereometric objects in space. If your math tutor is highly qualified, then he should know this. Otherwise, I would advise changing the tutor for the “C” part. My preparation for the Unified State Exam in mathematics C1-C6 usually includes an analysis of the basic algorithms and formulas described below.

Angle between lines a and b

The angle between lines in space is the angle between any intersecting lines parallel to them. This angle equal to angle between the direction vectors of these straight lines (or complements it to 180 degrees).

What algorithm does the math tutor use to find the angle?

1) Choose any vectors and having the directions of straight lines a and b (parallel to them).
2) We determine the coordinates of the vectors using the corresponding coordinates of their beginnings and ends (the coordinates of the beginning must be subtracted from the coordinates of the end of the vector).
3) Substitute the found coordinates into the formula:
. To find the angle itself, you need to find the arc cosine of the result.

Normal to plane

A normal to a plane is any vector perpendicular to that plane.
How to find normal? To find the coordinates of the normal, it is enough to know the coordinates of any three points M, N and K lying in a given plane. Using these coordinates, we find the coordinates of the vectors and and require that the conditions and be met. By equating the scalar product of vectors to zero, we create a system of equations with three variables, from which we can find the coordinates of the normal.

Math tutor's note : It is not at all necessary to solve the system completely, because it is enough to select at least one normal. To do this, you can substitute any number (for example, one) instead of any of its unknown coordinates and solve the system of two equations with the remaining two unknowns. If it has no solutions, then this means that in the family of normals there is no one whose value is one in the selected variable. Then substitute one for another variable (another coordinate) and solve new system. If you miss again, then your normal will have one at the last coordinate, and it itself will turn out to be parallel to some coordinate plane (in this case it is easy to find without a system).

Let's assume that we are given a straight line and a plane with the coordinates of the direction vector and normal
The angle between the straight line and the plane is calculated using the following formula:

Let and be any two normals to these planes. Then the cosine of the angle between the planes is equal to the modulus of the cosine of the angle between the normals:

Equation of a plane in space

Points satisfying the equality form a plane with a normal. The coefficient is responsible for the amount of deviation (parallel shift) between two planes with the same given normal. In order to write the equation of a plane, you must first find its normal (as described above), and then substitute the coordinates of any point on the plane along with the coordinates of the found normal into the equation and find the coefficient.

MOU average comprehensive school №13

Coordinate method

2008
Plan:

1. 
   Introduction
2. 
   
3. 
   The essence of the coordinate method
4. 
   Coordinate method systems
5. 
   Basic formulas of the coordinate method
6. 
   Problems of different levels of complexity on the topic “Coordinate Method”

(with detailed solutions)

1. 
   Conclusion
2. 
   Bibliography

Introduction

Used in geometry various methods problem solving is a synthetic (purely geometric) method, transformation method, vector method, coordinate method and others. They occupy different positions in the school. The main method is considered to be synthetic, and of the others, the coordinate method occupies the highest position because it is closely related to algebra. The elegance of the synthetic method is achieved with the help of intuition, guesswork, and additional constructions. The coordinate method does not require this: the solution of problems is largely algorithmic, which in most cases simplifies the search and solution of the problem itself.

Coordinate method- a way to determine the position of a point or body using numbers or other symbols.

Coordinate system- a set of definitions that implements the coordinate method, i.e. a way to determine the position of a point or body using numbers or other symbols.

Giving geometric studies an algebraic character, the coordinate method transfers the most important feature algebra - uniformity of ways to solve problems. If in arithmetic and elementary geometry one has, as a rule, to look for a special solution path for each problem, then in algebra and analytical geometry solutions are carried out according to a plan common to all problems, easily adaptable to any problem. The transfer of methods for solving problems that are characteristic of algebra and therefore have great generality to geometry is the main value of the coordinate method. Another advantage of the coordinate method is that its use eliminates the need to resort to visual representation of complex spatial images.

Objectives of studying the coordinate method

We can highlight the following goals for studying the coordinate method in a school geometry course:

• 
  give students effective method solving problems and proving a number of theorems;
• 
  show, based on this method, the close connection between algebra and geometry;
• 
  contribute to the development of computing and graphic culture of students.

The essence of the coordinate method

The essence of the coordinate method as a method for solving problems is that by specifying figures with equations and expressing various geometric relationships in coordinates, we can solve a geometric problem using algebra. Conversely, using coordinates, one can interpret algebraic and analytical relationships and facts geometrically and thus apply geometry to the solution of algebraic problems.

The coordinate method is a universal method.

In a relationship school course In geometry, we can say that in some cases the coordinate method makes it possible to construct proofs and solve many problems more rationally and beautifully than by purely geometric methods. The coordinate method is associated, however, with one geometric complexity. The same problem receives a different analytical representation depending on a particular choice of coordinate system. And only sufficient experience allows you to choose the most appropriate coordinate system.

Coordinate systems:
1. Rectangular (Cartesian) coordinate system (Descartes Rene (1596-1650))

Born in Turin into a wealthy noble family. A few days later, his mother died of consumption; his nurse came out and saved his life. At the age of 8, Rene was given full care to one of the best Jesuit colleges. Since childhood, Descartes loved solving problems and all his free time devoted himself to the study of mathematics. Descartes studied philosophy, mathematics, physics, astronomy, and philology. Descartes was the first to show how mathematics could be used to visualize and mathematical analysis for a wide variety of natural and social phenomena.

The following appear for the first time in his works:

1. 
   variables
2. 
   strict laws of geometry are translated into algebraic language
3. 
   it was proposed to depict connections between natural phenomena with curved lines and write them down in algebraic expressions
4. 
   Latin letters of constants and variables, as well as degree designations

2.Oblique coordinate system differs from a rectangular one in that its axes are not perpendicular. The coordinates of a point are determined as in a rectangular coordinate system along straight parallel axes.

3. Polar coordinate system . The polar coordinates of a point are determined as follows: a numerical ray OX is specified on the plane. The beginning of the ray, point O, is called the pole, and the OX axis is called the polar axis. To determine the position of point M in the polar coordinate system, indicate the distance from the pole to this point and the direction in which it is located. The distance from a point to a pole is called the polar radius of a point and is denoted by the letter (pronounced “roh”).

The direction is set by the angle of rotation from beam OX to beam OM

Coordinate method

formulas

Length of a vector based on its coordinates

Formula for finding the coordinates of the midpoint of a segment

Distance between two points

Equation of a circle,(circle center
,radius r)

Equation of a line
, given that
(the equation of a straight line in a rectangular coordinate system is an equation of the first degree)

Each straight line is given by an equation. Wherein numbers a,b,c are determined for each straight line uniquely up to proportionality (if you multiply them by the same number
, then the resulting equation
will define the same line).

Distance from point
to a straight line m
,equals

Distance from point
to plane
, equals

Derivation of the formula
.

Let's drop from the point
perpendicular AB to plane , given by the equation
.Let
- the point of intersection of this perpendicular with the plane . Then
- distance from point
to plane .Since the vector is perpendicular to the plane ,it is collinear to the vector
.It means that
,If
, or
,If
, that is
.Let's rewrite this equality in coordinates: .But the point
, That's why
And
=
.
(Stewart's theorem)

If triangle ABC is given and based on it the point D , lying between points B and C, then the equality is true:

Proof:

Let's choose a coordinate system as shown in the figure.

In the selected coordinate system, the vertices of the triangle ABC will have the following coordinates:

A(x 1 ;y 1 ), B(x 2 ;0), C(0;0) and period D(x 3 ;0) .

Let's calculate all the quantities included in the equality:

Let's substitute all these values ​​into left side equality:

Q.E.D.

Task 1. Find the distance from point A(-1,3,0) to the plane , given by the equation x -3y -2z +5=0.

Solution. According to the formula
we get:

.

Answer:
.

Problem 2. Vectors And mutually perpendicular, and the vector forms an angle of 60˚ with each of them. Knowing that
, calculate the scalar product

Solution. Using the property of the scalar product, let’s open the brackets:

=

From the definition of the scalar product we get:
(because And perpendicular);

Substituting these values ​​into the expression
=, we find the scalar product:
=0 – 50+9 12 -120=-62

Answer:
=0 – 50+9 12 -120=-62
Problem 3.Given a square ABCD with the side A . Determine the distance between the middle of the segment AM , Where M – middle Sun , and a point N on the side CD , dividing it so that CN:ND=3:1 .

Solution:

Let's choose a coordinate system as shown in the figure.

Then the points M And N , according to the condition, will have coordinates:

respectively.

Because E – middle AM , then its coordinates will be as follows:

Means, E .

Let's find the distance between points E And N :

Answer: EN =

Problem 4 Given a cube ABCDA1B1C1D1 with edges of length 1. Point E is taken on its side edge AA 1 so that
.Point F is taken on edge BC so that
A plane is drawn through the center of the cube and points E and F .Find the distance from vertex B to the plane .

Solution.

Let us introduce a coordinate system with center at vertex B. Then
Let's find the equation of the plane . Let this equation be . notice, that does not pass through the origin, so
and the equation can be divided by D; we get the following equation:
or ax + by + cz +1=0

To determine the unknown coefficients a, b and c, we substitute into the equation ax + by + cz +1=0 the coordinates of three points E, F and O that satisfy this equation (since these points lie in the plane ).We obtain a system of equations:
Let's transform the system by multiplying the first equation by 3, the second by 4, and the third by -6 and adding the first equation with the third we get
, b=-4,
.So the plane equation has the form:

5x + 8y - 9z – 2 =0. Now we find the distance from point B1(0,0,1) to the plane
.

Answer:
.

Problem 5.Base triangular pyramid SABC is an equilateral triangle ABC, the side of which is equal to 4. It is also known that AS = BS =
, and CS=3.Find the area of ​​the sphere circumscribed about this pyramid.