How to solve logarithmic equations and inequalities. Complex logarithmic inequalities
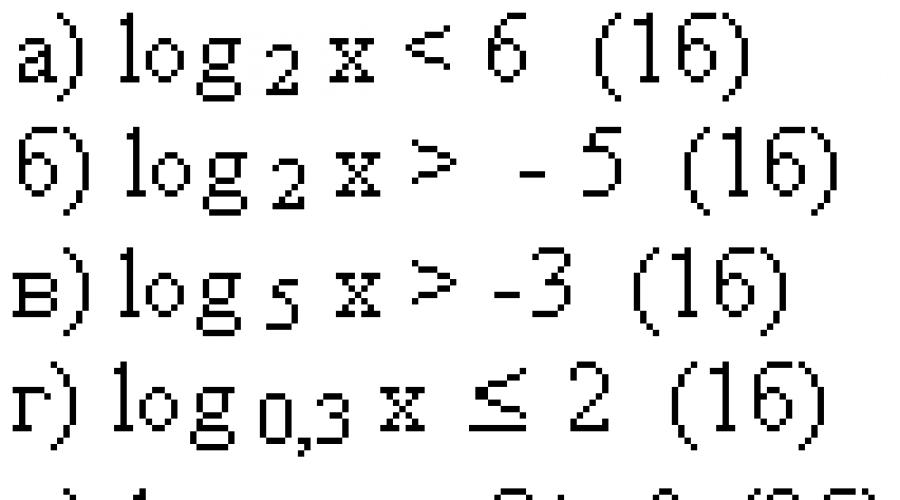
Read also
Lesson objectives:
Didactic:
- Level 1 – teach how to solve the simplest logarithmic inequalities, using the definition of a logarithm and the properties of logarithms;
- Level 2 – solve logarithmic inequalities, choosing your own solution method;
- Level 3 – be able to apply knowledge and skills in non-standard situations.
Educational: develop memory, attention, logical thinking, comparison skills, ability to generalize and draw conclusions
Educational: cultivate accuracy, responsibility for the task being performed, and mutual assistance.
Teaching methods: verbal , visual , practical , partial-search , self-government , control.
Forms of organization cognitive activity students: frontal , individual , work in pairs.
Equipment: a set of test tasks, reference summary, blank sheets for solutions.
Lesson type: learning new material.
During the classes
1. Organizational moment. The topic and goals of the lesson, the lesson plan are announced: each student is given an assessment sheet, which the student fills out during the lesson; for each pair of students - printed materials with tasks; tasks must be completed in pairs; blank solution sheets; support sheets: definition of logarithm; graph of a logarithmic function, its properties; properties of logarithms; solution algorithm logarithmic inequalities.
All decisions after self-assessment are submitted to the teacher.
Student's score sheet
2. Updating knowledge.
Teacher's instructions. Recall the definition of logarithm, the graph of the logarithmic function, and its properties. To do this, read the text on pp. 88–90, 98–101 of the textbook “Algebra and the beginnings of analysis 10–11” edited by Sh.A Alimov, Yu.M Kolyagin and others.
Students are given sheets on which are written: the definition of a logarithm; shows a graph of a logarithmic function and its properties; properties of logarithms; algorithm for solving logarithmic inequalities, an example of solving a logarithmic inequality that reduces to a quadratic one.
3. Studying new material.
Solving logarithmic inequalities is based on the monotonicity of the logarithmic function.
Algorithm for solving logarithmic inequalities:
A) Find the domain of definition of the inequality (the sublogarithmic expression is greater than zero).
B) Represent (if possible) the left and right sides of the inequality as logarithms to the same base.
C) Determine whether the logarithmic function: if t>1, then increasing; if 0
D) Go to more simple inequality(sublogarithmic expressions), taking into account that the inequality sign will remain if the function increases, and will change if it decreases.
Learning element #1.
Goal: consolidate the solution to the simplest logarithmic inequalities
Form of organization of students' cognitive activity: individual work.
Tasks for independent work for 10 minutes. For each inequality there are several possible answers; you need to choose the correct one and check it using the key.

KEY: 13321, maximum number of points – 6 points.
Learning element #2.
Goal: consolidate the solution of logarithmic inequalities using the properties of logarithms.
Teacher's instructions. Remember the basic properties of logarithms. To do this, read the text of the textbook on pp. 92, 103–104.
Tasks for independent work for 10 minutes.

KEY: 2113, maximum number of points – 8 points.
Learning element #3.
Purpose: to study the solution of logarithmic inequalities by the method of reduction to quadratic.
Teacher's instructions: the method of reducing an inequality to a quadratic is to transform the inequality to such a form that a certain logarithmic function is denoted by a new variable, thereby obtaining a quadratic inequality with respect to this variable.

Let's use the interval method.

You have passed the first level of mastering the material. Now you will have to independently choose a method for solving logarithmic equations, using all your knowledge and capabilities.
Learning element #4.
Goal: consolidate the solution to logarithmic inequalities by independently choosing a rational solution method.
Tasks for independent work for 10 minutes

Learning element #5.
Teacher's instructions. Well done! You have mastered solving equations of the second level of complexity. The goal of your further work is to apply your knowledge and skills in more complex and non-standard situations.
Tasks for independent solution:

Teacher's instructions. It's great if you completed the whole task. Well done!
The grade for the entire lesson depends on the number of points scored for all educational elements:
- if N ≥ 20, then you get a “5” rating,
- for 16 ≤ N ≤ 19 – score “4”,
- for 8 ≤ N ≤ 15 – score “3”,
- at N< 8 выполнить работу над ошибками к следующему уроку (решения можно взять у учителя).
Submit the assessment papers to the teacher.
5. Homework: if you scored no more than 15 points, work on your mistakes (solutions can be taken from the teacher), if you scored more than 15 points, complete a creative task on the topic “Logarithmic inequalities.”
With them are inside logarithms.
Examples:
\(\log_3x≥\log_39\)
\(\log_3 ((x^2-3))< \log_3{(2x)}\)
\(\log_(x+1)((x^2+3x-7))>2\)
\(\lg^2((x+1))+10≤11 \lg((x+1))\)
How to solve logarithmic inequalities:
We should strive to reduce any logarithmic inequality to the form \(\log_a(f(x)) ˅ \log_a(g(x))\) (the symbol \(˅\) means any of ). This type allows you to get rid of logarithms and their bases, making the transition to the inequality of expressions under logarithms, that is, to the form \(f(x) ˅ g(x)\).
But when making this transition there is one very important subtlety:
\(-\) if is a number and it is greater than 1, the inequality sign remains the same during the transition,
\(-\) if the base is a number greater than 0 but less than 1 (lies between zero and one), then the inequality sign should change to the opposite, i.e.
|
\(\log_2((8-x))<1\) Solution: |
\(\log\)\(_(0.5)\) \((2x-4)\)≥\(\log\)\(_(0.5)\) \(((x+ 1))\) Solution: |
Very important! In any inequality, the transition from the form \(\log_a(f(x)) ˅ \log_a(g(x))\) to comparing expressions under logarithms can be done only if:
Example . Solve inequality: \(\log\)\(≤-1\)
Solution:
|
\(\log\) \(_(\frac(1)(3))(\frac(3x-2)(2x-3))\)\(≤-1\) |
Let's write out the ODZ. |
|
ODZ: \(\frac(3x-2)(2x-3)\) \(>0\) |
|
|
\(\frac(3x-2-3(2x-3))(2x-3)\)\(≥\) \(0\) |
We open the brackets and bring . |
|
\(\frac(-3x+7)(2x-3)\) \(≥\) \(0\) |
We multiply the inequality by \(-1\), not forgetting to reverse the comparison sign. |
|
\(\frac(3x-7)(2x-3)\) \(≤\) \(0\) |
|
|
\(\frac(3(x-\frac(7)(3)))(2(x-\frac(3)(2)))\)\(≤\) \(0\) |
Let's construct a number line and mark the points \(\frac(7)(3)\) and \(\frac(3)(2)\) on it. Please note that the point from the denominator is removed, despite the fact that the inequality is not strict. The fact is that this point will not be a solution, since when substituted into inequality it will lead us to division by zero. |
|
|
Now we plot the ODZ on the same numerical axis and write down in response the interval that falls into the ODZ. |
|
|
We write down the final answer. |
Example . Solve the inequality: \(\log^2_3x-\log_3x-2>0\)
Solution:
|
\(\log^2_3x-\log_3x-2>0\) |
Let's write out the ODZ. |
|
ODZ: \(x>0\) |
Let's get to the solution. |
|
Solution: \(\log^2_3x-\log_3x-2>0\) |
Here we have a typical square-logarithmic inequality. Let's do it. |
|
\(t=\log_3x\) |
Lay out left side inequalities on . |
|
\(D=1+8=9\) |
|
|
Now we need to return to the original variable - x. To do this, let's go to , which has the same solution, and make the reverse substitution. |
|
|
\(\left[ \begin(gathered) t>2 \\ t<-1 \end{gathered} \right.\) \(\Leftrightarrow\) \(\left[ \begin{gathered} \log_3x>2\\\log_3x<-1 \end{gathered} \right.\) |
Transform \(2=\log_39\), \(-1=\log_3\frac(1)(3)\). |
|
\(\left[ \begin(gathered) \log_3x>\log_39 \\ \log_3x<\log_3\frac{1}{3} \end{gathered} \right.\) |
Let's move on to comparing arguments. The bases of logarithms are greater than \(1\), so the sign of the inequalities does not change. |
|
\(\left[ \begin(gathered) x>9 \\ x<\frac{1}{3} \end{gathered} \right.\) |
Let us combine the solution to the inequality and the ODZ in one figure. |
|
|
Let's write down the answer. |
An inequality is called logarithmic if it contains a logarithmic function.
Methods for solving logarithmic inequalities are no different from, except for two things.
Firstly, when moving from the logarithmic inequality to the inequality of sublogarithmic functions, one should follow the sign of the resulting inequality. It obeys the following rule.
If the base of the logarithmic function is greater than $1$, then when moving from the logarithmic inequality to the inequality of sublogarithmic functions, the sign of the inequality is preserved, but if it is less than $1$, then it changes to the opposite.
Secondly, the solution to any inequality is an interval, and, therefore, at the end of solving the inequality of sublogarithmic functions it is necessary to create a system of two inequalities: the first inequality of this system will be the inequality of sublogarithmic functions, and the second will be the interval of the domain of definition of the logarithmic functions included in the logarithmic inequality.
Practice.
Let's solve the inequalities:
1. $\log_(2)((x+3)) \geq 3.$
$D(y): \x+3>0.$
$x \in (-3;+\infty)$
The base of the logarithm is $2>1$, so the sign does not change. Using the definition of logarithm, we get:
$x+3 \geq 2^(3),$
$x \in )


