Investigate linear dependence of a system of vectors online. Linear dependence of a system of vectors. Collinear vectors
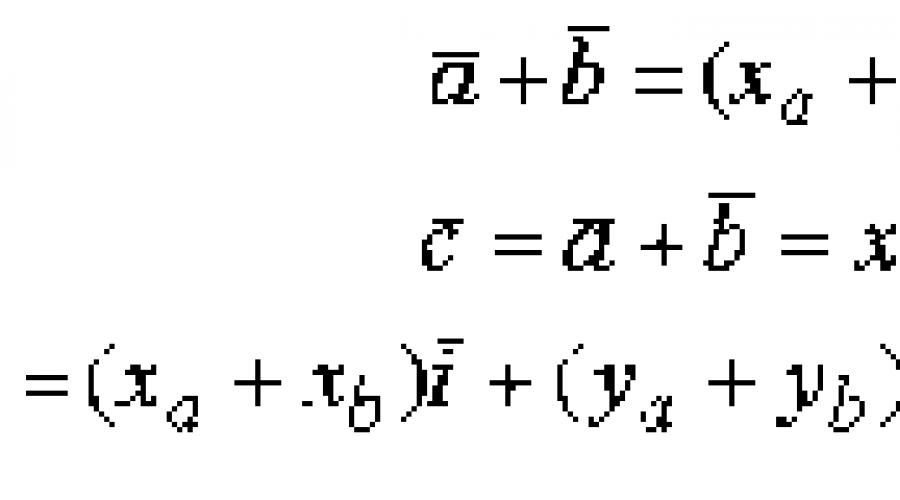
Read also
Vectors, their properties and actions with them
Vectors, actions with vectors, linear vector space.
Vectors are an ordered collection of a finite number of real numbers.
Actions: 1.Multiplying a vector by a number: lambda*vector x=(lamda*x 1, lambda*x 2 ... lambda*x n).(3.4, 0, 7)*3=(9, 12,0.21)
2. Addition of vectors (belong to the same vector space) vector x + vector y = (x 1 + y 1, x 2 + y 2, ... x n + y n,)
3. Vector 0=(0,0…0)---n E n – n-dimensional (linear space) vector x + vector 0 = vector x
Theorem. In order for a system of n vectors, an n-dimensional linear space, to be linearly dependent, it is necessary and sufficient that one of the vectors be a linear combination of the others.
Theorem. Any set of n+ 1st vectors of n-dimensional linear space of phenomena. linearly dependent.
Addition of vectors, multiplication of vectors by numbers. Subtraction of vectors.
The sum of two vectors is a vector directed from the beginning of the vector to the end of the vector, provided that the beginning coincides with the end of the vector. If vectors are given by their expansions in basis unit vectors, then when adding vectors, their corresponding coordinates are added.
Let's consider this using the example of a Cartesian coordinate system. Let
Let's show that

From Figure 3 it is clear that ![]()

The sum of any finite number of vectors can be found using the polygon rule (Fig. 4): to construct the sum of a finite number of vectors, it is enough to combine the beginning of each subsequent vector with the end of the previous one and construct a vector connecting the beginning of the first vector with the end of the last.

Properties of the vector addition operation:
In these expressions m, n are numbers.
The difference between vectors is called a vector. The second term is a vector opposite to the vector in direction, but equal to it in length.

Thus, the operation of subtracting vectors is replaced by an addition operation
A vector whose beginning is at the origin and end at point A (x1, y1, z1) is called the radius vector of point A and is denoted simply. Since its coordinates coincide with the coordinates of point A, its expansion in unit vectors has the form

A vector that starts at point A(x1, y1, z1) and ends at point B(x2, y2, z2) can be written as ![]()
where r 2 is the radius vector of point B; r 1 - radius vector of point A.
Therefore, the expansion of the vector in unit vectors has the form
Its length is equal to the distance between points A and B
MULTIPLICATION
So in the case plane problem the product of a vector by a = (ax; ay) by the number b is found by the formula
a b = (ax b; ay b)
Example 1. Find the product of the vector a = (1; 2) by 3.
3 a = (3 1; 3 2) = (3; 6)
So, in the case of a spatial problem, the product of the vector a = (ax; ay; az) by the number b is found by the formula
a b = (ax b; ay b; az b)
Example 1. Find the product of the vector a = (1; 2; -5) by 2.
2 a = (2 1; 2 2; 2 (-5)) = (2; 4; -10)
Dot product of vectors and ![]() where is the angle between the vectors and ; if either, then
where is the angle between the vectors and ; if either, then
From the definition of the scalar product it follows that ![]()
where, for example, is the magnitude of the projection of the vector onto the direction of the vector.
Scalar squared vector:
Properties of the dot product:
![]()
![]()
![]()
![]()
Dot product in coordinates
If ![]()
![]() That
That ![]()
Angle between vectors
Angle between vectors - the angle between the directions of these vectors (smallest angle).
Cross product (Cross product of two vectors.) - this is a pseudovector perpendicular to a plane constructed from two factors, which is the result of the binary operation “vector multiplication” over vectors in three-dimensional Euclidean space. The product is neither commutative nor associative (it is anticommutative) and is different from the dot product of vectors. In many engineering and physics problems, you need to be able to construct a vector perpendicular to two existing ones - the vector product provides this opportunity. The cross product is useful for "measuring" the perpendicularity of vectors - the length of the cross product of two vectors is equal to the product of their lengths if they are perpendicular, and decreases to zero if the vectors are parallel or antiparallel.
The cross product is defined only in three-dimensional and seven-dimensional spaces. The result of a vector product, like a scalar product, depends on the metric of Euclidean space.
Unlike the formula for calculating scalar product vectors from coordinates in a three-dimensional rectangular coordinate system, the formula for the cross product depends on the orientation of the rectangular coordinate system or, in other words, its “chirality”
Collinearity of vectors.
Two non-zero (not equal to 0) vectors are called collinear if they lie on parallel lines or on the same line. An acceptable, but not recommended, synonym is “parallel” vectors. Collinear vectors can be identically directed ("codirectional") or oppositely directed (in the latter case they are sometimes called "anticollinear" or "antiparallel").
Mixed product of vectors( a, b, c)- scalar product of vector a and the vector product of vectors b and c:
(a,b,c)=a ⋅(b ×c)
it is sometimes called the triple dot product of vectors, apparently because the result is a scalar (more precisely, a pseudoscalar).
Geometric meaning: The modulus of the mixed product is numerically equal to the volume of the parallelepiped formed by the vectors (a,b,c) .
Properties
Mixed piece skew-symmetric with respect to all its arguments: i.e. e. rearranging any two factors changes the sign of the product. It follows that the Mixed product in the right Cartesian coordinate system (in an orthonormal basis) is equal to the determinant of a matrix composed of vectors and:
The mixed product in the left Cartesian coordinate system (in an orthonormal basis) is equal to the determinant of the matrix composed of vectors and, taken with a minus sign:
In particular,
If any two vectors are parallel, then with any third vector they form a mixed product equal to zero.
If three vectors are linearly dependent (that is, coplanar, lying in the same plane), then their mixed product is equal to zero.
Geometric sense - Mixed product by absolute value equal to the volume of the parallelepiped (see figure) formed by the vectors and; the sign depends on whether this triple of vectors is right-handed or left-handed.
Coplanarity of vectors.
Three vectors (or a larger number) are called coplanar if they, being reduced to a common origin, lie in the same plane
Properties of coplanarity
If at least one of three vectors- zero, then the three vectors are also considered coplanar.
A triple of vectors containing a pair of collinear vectors is coplanar.
Mixed product of coplanar vectors. This is a criterion for the coplanarity of three vectors.
Coplanar vectors are linearly dependent. This is also a criterion for coplanarity.
In 3-dimensional space, 3 non-coplanar vectors form a basis
Linearly dependent and linearly independent vectors.
Linearly dependent and independent vector systems.Definition. The vector system is called linearly dependent, if there is at least one nontrivial linear combination of these vectors equal to the zero vector. Otherwise, i.e. if only a trivial linear combination of given vectors equals the null vector, the vectors are called linearly independent.
Theorem (linear dependence criterion). In order for a system of vectors in a linear space to be linearly dependent, it is necessary and sufficient that at least one of these vectors is a linear combination of the others.
1) If among the vectors there is at least one zero vector, then the entire system of vectors is linearly dependent.
In fact, if, for example, , then, assuming , we have a nontrivial linear combination .▲
2) If among the vectors some form a linearly dependent system, then the entire system is linearly dependent.
Indeed, let the vectors , , be linearly dependent. This means that there is a non-trivial linear combination equal to the zero vector. But then, assuming ![]() , we also obtain a nontrivial linear combination equal to the zero vector.
, we also obtain a nontrivial linear combination equal to the zero vector.
2. Basis and dimension. Definition. System of linearly independent vectors ![]() vector space is called basis of this space if any vector from can be represented as a linear combination of vectors of this system, i.e. for each vector there are real numbers
vector space is called basis of this space if any vector from can be represented as a linear combination of vectors of this system, i.e. for each vector there are real numbers ![]() such that the equality holds. This equality is called vector decomposition according to the basis, and the numbers
such that the equality holds. This equality is called vector decomposition according to the basis, and the numbers ![]() are called coordinates of the vector relative to the basis(or in the basis) .
are called coordinates of the vector relative to the basis(or in the basis) .
Theorem (on the uniqueness of the expansion with respect to the basis). Every vector in space can be expanded into a basis in the only way, i.e. coordinates of each vector in the basis are determined unambiguously.
Task 1. Find out whether the system of vectors is linearly independent. The system of vectors will be specified by the matrix of the system, the columns of which consist of the coordinates of the vectors.
 .
.
Solution. Let the linear combination  equal to zero. Having written this equality in coordinates, we obtain the following system of equations:
equal to zero. Having written this equality in coordinates, we obtain the following system of equations:
 .
.
Such a system of equations is called triangular. She has only one solution  . Therefore, the vectors
. Therefore, the vectors  linearly independent.
linearly independent.
Task 2. Find out whether it is linear independent system vectors.
 .
.
Solution. Vectors  are linearly independent (see problem 1). Let us prove that the vector is a linear combination of vectors
are linearly independent (see problem 1). Let us prove that the vector is a linear combination of vectors  . Vector expansion coefficients
. Vector expansion coefficients  are determined from the system of equations
are determined from the system of equations
 .
.
This system, like a triangular one, has a unique solution.
Therefore, the system of vectors  linearly dependent.
linearly dependent.
Comment. Matrices of the same type as in Problem 1 are called triangular , and in problem 2 – stepped triangular . The question of the linear dependence of a system of vectors is easily resolved if the matrix composed of the coordinates of these vectors is step triangular. If the matrix does not have special type, then using elementary string conversions , preserving linear relationships between the columns, it can be reduced to a step-triangular form.
Elementary transformations lines matrices (EPS) the following operations on a matrix are called:
1) rearrangement of lines;
2) multiplying a string by a non-zero number;
3) adding another string to a string, multiplied by an arbitrary number.
Task 3. Find the maximum linearly independent subsystem and calculate the rank of the system of vectors
 .
.
Solution. Let us reduce the matrix of the system using EPS to a step-triangular form. To explain the procedure, we denote the line with the number of the matrix to be transformed by the symbol . The column after the arrow indicates the actions on the rows of the matrix being converted that must be performed to obtain the rows of the new matrix.

 .
.
Obviously, the first two columns of the resulting matrix are linearly independent, the third column is their linear combination, and the fourth does not depend on the first two. Vectors  are called basic. They form a maximal linearly independent subsystem of the system
are called basic. They form a maximal linearly independent subsystem of the system  , and the rank of the system is three.
, and the rank of the system is three.
Basis, coordinates
Task 4. Find the basis and coordinates of the vectors in this basis on the set of geometric vectors whose coordinates satisfy the condition  .
.
Solution. The set is a plane passing through the origin. An arbitrary basis on a plane consists of two non-collinear vectors. The coordinates of the vectors in the selected basis are determined by the solution of the corresponding system linear equations.
There is another way to solve this problem, when you can find the basis using the coordinates.
Coordinates  spaces are not coordinates on the plane, since they are related by the relation
spaces are not coordinates on the plane, since they are related by the relation  , that is, they are not independent. The independent variables and (they are called free) uniquely define a vector on the plane and, therefore, they can be chosen as coordinates in . Then the basis
, that is, they are not independent. The independent variables and (they are called free) uniquely define a vector on the plane and, therefore, they can be chosen as coordinates in . Then the basis  consists of vectors lying in and corresponding to sets of free variables
consists of vectors lying in and corresponding to sets of free variables  And
And  , that is .
, that is .
Task 5. Find the basis and coordinates of the vectors in this basis on the set of all vectors in space whose odd coordinates are equal to each other.
Solution. Let us choose, as in the previous problem, coordinates in space.
Because  , then free variables
, then free variables  uniquely determine the vector from and are therefore coordinates. The corresponding basis consists of vectors.
uniquely determine the vector from and are therefore coordinates. The corresponding basis consists of vectors.
Task 6. Find the basis and coordinates of the vectors in this basis on the set of all matrices of the form  , Where
, Where  – arbitrary numbers.
– arbitrary numbers.
Solution. Each matrix from is uniquely representable in the form:
This relation is the expansion of the vector from with respect to the basis  with coordinates
with coordinates  .
.
Task 7. Find the dimension and basis of the linear hull of a system of vectors
 .
.
Solution. Using the EPS, we transform the matrix from the coordinates of the system vectors to a step-triangular form.


 .
.
Columns  the last matrices are linearly independent, and the columns
the last matrices are linearly independent, and the columns  linearly expressed through them. Therefore, the vectors
linearly expressed through them. Therefore, the vectors  form a basis
form a basis  , And
, And  .
.
Comment. Basis in  is chosen ambiguously. For example, vectors
is chosen ambiguously. For example, vectors  also form a basis
also form a basis  .
.
a 1 = { 3, 5, 1 , 4 }, a 2 = { –2, 1, -5 , -7 }, a 3 = { -1, –2, 0, –1 }.
Solution. Are looking for common decision systems of equations
a 1 x 1 + a 2 x 2 + a 3 x 3 = Θ
Gauss method. To do this, we write this homogeneous system in coordinates:
System Matrix
The allowed system has the form: ![]() (r A = 2, n= 3). The system is cooperative and uncertain. Its general solution ( x 2 – free variable): x 3 = 13x 2 ; 3x 1 – 2x 2 – 13x 2 = 0 => x 1 = 5x 2 => X o = . The presence of a non-zero particular solution, for example, indicates that the vectors a
1 , a
2 , a
3
linearly dependent.
(r A = 2, n= 3). The system is cooperative and uncertain. Its general solution ( x 2 – free variable): x 3 = 13x 2 ; 3x 1 – 2x 2 – 13x 2 = 0 => x 1 = 5x 2 => X o = . The presence of a non-zero particular solution, for example, indicates that the vectors a
1 , a
2 , a
3
linearly dependent.
Example 2.
Find out whether this system linearly dependent or linearly independent vectors:
1. a 1 = { -20, -15, - 4 }, a 2 = { –7, -2, -4 }, a 3 = { 3, –1, –2 }.
Solution. Consider a homogeneous system of equations a 1 x 1 + a 2 x 2 + a 3 x 3 = Θ
or in expanded form (by coordinates)

The system is homogeneous. If it is non-degenerate, then it has a unique solution. In the case of a homogeneous system, there is a zero (trivial) solution. This means that in this case the system of vectors is independent. If the system is degenerate, then it has non-zero solutions and, therefore, it is dependent.
We check the system for degeneracy:
 = –80 – 28 + 180 – 48 + 80 – 210 = – 106 ≠ 0.
= –80 – 28 + 180 – 48 + 80 – 210 = – 106 ≠ 0.
The system is non-degenerate and, thus, the vectors a 1 , a 2 , a 3 linearly independent.
Tasks. Find out whether a given system of vectors is linearly dependent or linearly independent:
1. a 1 = { -4, 2, 8 }, a 2 = { 14, -7, -28 }.
2. a 1 = { 2, -1, 3, 5 }, a 2 = { 6, -3, 3, 15 }.
3. a 1 = { -7, 5, 19 }, a 2 = { -5, 7 , -7 }, a 3 = { -8, 7, 14 }.
4. a 1 = { 1, 2, -2 }, a 2 = { 0, -1, 4 }, a 3 = { 2, -3, 3 }.
5. a 1 = { 1, 8 , -1 }, a 2 = { -2, 3, 3 }, a 3 = { 4, -11, 9 }.
6. a 1 = { 1, 2 , 3 }, a 2 = { 2, -1 , 1 }, a 3 = { 1, 3, 4 }.
7. a 1 = {0, 1, 1 , 0}, a 2 = {1, 1 , 3, 1}, a 3 = {1, 3, 5, 1}, a 4 = {0, 1, 1, -2}.
8. a 1 = {-1, 7, 1 , -2}, a 2 = {2, 3 , 2, 1}, a 3 = {4, 4, 4, -3}, a 4 = {1, 6, -11, 1}.
9. Prove that a system of vectors will be linearly dependent if it contains:
a) two equal vectors;
b) two proportional vectors.
Definition. Linear combination of vectors a 1 , ..., a n with coefficients x 1 , ..., x n is called a vector
x 1 a 1 + ... + x n a n .
trivial, if all coefficients x 1 , ..., x n are equal to zero.
Definition. The linear combination x 1 a 1 + ... + x n a n is called non-trivial, if at least one of the coefficients x 1, ..., x n is not equal to zero.
linearly independent, if there is no non-trivial combination of these vectors equal to the zero vector.
That is, the vectors a 1, ..., a n are linearly independent if x 1 a 1 + ... + x n a n = 0 if and only if x 1 = 0, ..., x n = 0.
Definition. The vectors a 1, ..., a n are called linearly dependent, if there is a non-trivial combination of these vectors equal to the zero vector.
Properties of linearly dependent vectors:
For n-dimensional vectors.
n + 1 vectors are always linearly dependent.
For 2 and 3 dimensional vectors.
Two linear dependent vectors- collinear. (Collinear vectors are linearly dependent.)
For 3-dimensional vectors.
Three linearly dependent vectors are coplanar. (Three coplanar vectors are linearly dependent.)
Examples of problems on linear dependence and linear independence of vectors:
Example 1. Check whether the vectors a = (3; 4; 5), b = (-3; 0; 5), c = (4; 4; 4), d = (3; 4; 0) are linearly independent.
Solution:
The vectors will be linearly dependent, since the dimension of the vectors is less than the number of vectors.
Example 2. Check whether the vectors a = (1; 1; 1), b = (1; 2; 0), c = (0; -1; 1) are linearly independent.
Solution:
| x 1 + x 2 = 0 | |
| x 1 + 2x 2 - x 3 = 0 | |
| x 1 + x 3 = 0 |
| 1 | 1 | 0 | 0 | ~ | ||
| 1 | 2 | -1 | 0 | |||
| 1 | 0 | 1 | 0 |
| ~ | 1 | 1 | 0 | 0 | ~ | 1 | 1 | 0 | 0 | ~ | ||||
| 1 - 1 | 2 - 1 | -1 - 0 | 0 - 0 | 0 | 1 | -1 | 0 | |||||||
| 1 - 1 | 0 - 1 | 1 - 0 | 0 - 0 | 0 | -1 | 1 | 0 |
subtract the second from the first line; add a second line to the third line:
| ~ | 1 - 0 | 1 - 1 | 0 - (-1) | 0 - 0 | ~ | 1 | 0 | 1 | 0 | ||||
| 0 | 1 | -1 | 0 | 0 | 1 | -1 | 0 | ||||||
| 0 + 0 | -1 + 1 | 1 + (-1) | 0 + 0 | 0 | 0 | 0 | 0 |
This solution shows that the system has many solutions, that is, there is a non-zero combination of values of the numbers x 1, x 2, x 3 such that the linear combination of vectors a, b, c is equal to the zero vector, for example:
A + b + c = 0
which means the vectors a, b, c are linearly dependent.
Answer: vectors a, b, c are linearly dependent.
Example 3. Check whether the vectors a = (1; 1; 1), b = (1; 2; 0), c = (0; -1; 2) are linearly independent.
Solution: Let us find the values of the coefficients at which the linear combination of these vectors will be equal to the zero vector.
x 1 a + x 2 b + x 3 c 1 = 0This vector equation can be written as a system of linear equations
| x 1 + x 2 = 0 | |
| x 1 + 2x 2 - x 3 = 0 | |
| x 1 + 2x 3 = 0 |
Let's solve this system using the Gauss method
| 1 | 1 | 0 | 0 | ~ | ||
| 1 | 2 | -1 | 0 | |||
| 1 | 0 | 2 | 0 |
subtract the first from the second line; subtract the first from the third line:
| ~ | 1 | 1 | 0 | 0 | ~ | 1 | 1 | 0 | 0 | ~ | ||||
| 1 - 1 | 2 - 1 | -1 - 0 | 0 - 0 | 0 | 1 | -1 | 0 | |||||||
| 1 - 1 | 0 - 1 | 2 - 0 | 0 - 0 | 0 | -1 | 2 | 0 |
subtract the second from the first line; add a second to the third line.