Fractionally rational. Solving integer and fractional rational equations
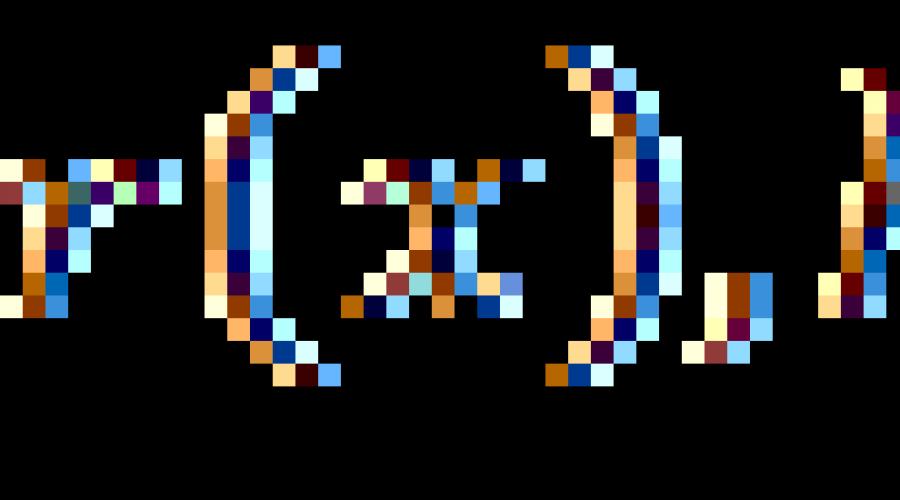
Read also
« Rational equations with polynomials" is one of the most common topics in test Unified State Exam assignments mathematics. For this reason, they are worth repeating Special attention. Many students are faced with the problem of finding the discriminant, transferring indicators from the right side to the left and bringing the equation to a common denominator, which is why completing such tasks causes difficulties. Solving rational equations in preparation for the Unified State Exam on our website will help you quickly cope with problems of any complexity and pass the test with flying colors.
Choose the Shkolkovo educational portal to successfully prepare for the Unified Mathematics Exam!
To know the rules for calculating unknowns and easily obtain correct results, use our online service. The Shkolkovo portal is a one-of-a-kind platform that contains everything necessary to prepare for Unified State Exam materials. Our teachers systematized and presented in an understandable form all the mathematical rules. In addition, we invite schoolchildren to try their hand at solving standard rational equations, the basis of which is constantly updated and expanded.
For more effective preparation for testing, we recommend following our special method and start by repeating the rules and solutions simple tasks, gradually moving on to more complex ones. Thus, the graduate will be able to identify the most difficult topics for himself and focus on studying them.
Start preparing for the final test with Shkolkovo today, and the results will not be long in coming! Choose the easiest example from those given. If you mastered the expression quickly, move on to more difficult task. This way you can improve your knowledge up to the point of solving USE tasks in mathematics at a specialized level.
Training is available not only to graduates from Moscow, but also to schoolchildren from other cities. Spend a couple of hours a day studying on our portal, for example, and very soon you will be able to cope with equations of any complexity!
We have already learned how to solve quadratic equations. Now let's extend the studied methods to rational equations.
What is a rational expression? We have already encountered this concept. Rational expressions are expressions made up of numbers, variables, their powers and symbols of mathematical operations.
Accordingly, rational equations are equations of the form: , where 
- rational expressions.
Previously, we considered only those rational equations that can be reduced to linear ones. Now let's consider those rational equations that can be reduced to quadratic ones.
Example 1
Solve the equation: .
Solution:
A fraction is equal to 0 if and only if its numerator is equal to 0 and its denominator is not equal to 0.
We get the following system:
The first equation of the system is quadratic equation. Before solving it, let's divide all its coefficients by 3. We get:
We get two roots: ; .
Since 2 never equals 0, two conditions must be met: 
. Since none of the roots of the equation obtained above coincides with the invalid values of the variable that were obtained when solving the second inequality, they are both solutions given equation.
Answer:.
So, let's formulate an algorithm for solving rational equations:
1. Transfer all terms to left side, so that the right side turns out to be 0.
2. Transform and simplify the left side, bring all fractions to a common denominator.
3. Equate the resulting fraction to 0 using the following algorithm: 
.
4. Write down those roots that were obtained in the first equation and satisfy the second inequality in the answer.
Let's look at another example.
Example 2
Solve the equation: 
.
Solution
At the very beginning, we move all the terms to the left so that 0 remains on the right. We get:
Now let's bring the left side of the equation to a common denominator:
This equation is equivalent to the system:
The first equation of the system is a quadratic equation.
Coefficients of this equation: . We calculate the discriminant:
We get two roots: ; .
Now let's solve the second inequality: the product of factors is not equal to 0 if and only if none of the factors is equal to 0.
Two conditions must be met: 
. We find that of the two roots of the first equation, only one is suitable - 3.
Answer:.
In this lesson, we remembered what a rational expression is, and also learned how to solve rational equations, which reduce to quadratic equations.
In the next lesson we will look at rational equations as models of real situations, and also look at motion problems.
Bibliography
- Bashmakov M.I. Algebra, 8th grade. - M.: Education, 2004.
- Dorofeev G.V., Suvorova S.B., Bunimovich E.A. and others. Algebra, 8. 5th ed. - M.: Education, 2010.
- Nikolsky S.M., Potapov M.A., Reshetnikov N.N., Shevkin A.V. Algebra, 8th grade. Tutorial for educational institutions. - M.: Education, 2006.
- Festival pedagogical ideas "Public lesson" ().
- School.xvatit.com ().
- Rudocs.exdat.com ().
§ 1 Integer and fractional rational equations
In this lesson we will look at concepts such as rational equation, rational expression, whole expression, fractional expression. Let's consider solving rational equations.
A rational equation is an equation in which the left and right sides are rational expressions.
Rational expressions are:
Fractional.
An integer expression is made up of numbers, variables, integer powers using the operations of addition, subtraction, multiplication, and division by a number other than zero.
For example:
Fractional expressions involve division by a variable or an expression with a variable. For example:
A fractional expression does not make sense for all values of the variables included in it. For example, the expression
at x = -9 it does not make sense, since at x = -9 the denominator goes to zero.
This means that a rational equation can be integer or fractional.
A whole rational equation is a rational equation in which the left and right sides are whole expressions.
For example:
A fractional rational equation is a rational equation in which either the left or right sides are fractional expressions.
For example:
§ 2 Solution of an entire rational equation
Let's consider the solution of an entire rational equation.
For example:
Multiply both sides of the equation by the smallest common denominator denominators of the fractions included in it.
For this:
1. find the common denominator for denominators 2, 3, 6. It is equal to 6;
2. find an additional factor for each fraction. To do this, divide the common denominator 6 by each denominator
additional factor for fraction
additional factor for fraction
3. multiply the numerators of the fractions by their corresponding additional factors. Thus, we obtain the equation
which is equivalent to the given equation
Let's open the brackets on the left, move the right part to the left, changing the sign of the term when transferred to the opposite one.
Let us bring similar terms of the polynomial and get
We see that the equation is linear.
Having solved it, we find that x = 0.5.
§ 3 Solution of a fractional rational equation
Let's consider solving a fractional rational equation.
For example:
1.Multiply both sides of the equation by the least common denominator of the denominators of the rational fractions included in it.
Let's find the common denominator for the denominators x + 7 and x - 1.
It is equal to their product (x + 7)(x - 1).
2. Let's find an additional factor for each rational fraction.
To do this, divide the common denominator (x + 7)(x - 1) by each denominator. Additional multiplier for fractions
equal to x - 1,
additional factor for fraction
equals x+7.
3.Multiply the numerators of the fractions by their corresponding additional factors.
We obtain the equation (2x - 1)(x - 1) = (3x + 4)(x + 7), which is equivalent to this equation
4.Multiply the binomial by the binomial on the left and right and get the following equation
5. We move the right side to the left, changing the sign of each term when transferring to the opposite:
6. Let us present similar terms of the polynomial:
7. Both sides can be divided by -1. We get a quadratic equation:
8. Having solved it, we will find the roots
Since in Eq.
the left and right sides are fractional expressions, and in fractional expressions, for some values of the variables, the denominator can become zero, then it is necessary to check whether the common denominator does not go to zero when x1 and x2 are found.
At x = -27, the common denominator (x + 7)(x - 1) does not vanish; at x = -1, the common denominator is also not zero.
Therefore, both roots -27 and -1 are roots of the equation.
When solving a fractional rational equation, it is better to immediately indicate the region acceptable values. Eliminate those values at which the common denominator goes to zero.
Let's consider another example of solving a fractional rational equation.
For example, let's solve the equation
We factor the denominator of the fraction on the right side of the equation
We get the equation
Let's find the common denominator for the denominators (x - 5), x, x(x - 5).
It will be the expression x(x - 5).
Now let's find the range of acceptable values of the equation
To do this, we equate the common denominator to zero x(x - 5) = 0.
We obtain an equation, solving which we find that at x = 0 or at x = 5 the common denominator goes to zero.
This means that x = 0 or x = 5 cannot be the roots of our equation.
Additional multipliers can now be found.
An additional factor for rational fractions
additional factor for the fraction
will be (x - 5),
and the additional factor of the fraction
We multiply the numerators by the corresponding additional factors.
We get the equation x(x - 3) + 1(x - 5) = 1(x + 5).
Let's open the brackets on the left and right, x2 - 3x + x - 5 = x + 5.
Let's move the terms from right to left, changing the sign of the transferred terms:
X2 - 3x + x - 5 - x - 5 = 0
And after bringing similar terms, we obtain a quadratic equation x2 - 3x - 10 = 0. Having solved it, we find the roots x1 = -2; x2 = 5.
But we have already found out that at x = 5 the common denominator x(x - 5) goes to zero. Therefore, the root of our equation
will be x = -2.
§ 4 Brief summary lesson
Important to remember:
When solving fractional rational equations, proceed as follows:
1. Find the common denominator of the fractions included in the equation. Moreover, if the denominators of fractions can be factored, then factor them and then find the common denominator.
2.Multiply both sides of the equation by a common denominator: find additional factors, multiply the numerators by additional factors.
3.Solve the resulting whole equation.
4. Eliminate from its roots those that make the common denominator vanish.
List of used literature:
- Makarychev Yu.N., N.G. Mindyuk, Neshkov K.I., Suvorova S.B. / Edited by Telyakovsky S.A. Algebra: textbook. for 8th grade. general education institutions. - M.: Education, 2013.
- Mordkovich A.G. Algebra. 8th grade: In two parts. Part 1: Textbook. for general education institutions. - M.: Mnemosyne.
- Rurukin A.N. Lesson developments in algebra: 8th grade. - M.: VAKO, 2010.
- Algebra 8th grade: lesson plans based on the textbook by Yu.N. Makarycheva, N.G. Mindyuk, K.I. Neshkova, S.B. Suvorova / Auth.-comp. T.L. Afanasyeva, L.A. Tapilina. -Volgograd: Teacher, 2005.
We introduced the equation above in § 7. First, let us recall what a rational expression is. This is an algebraic expression made up of numbers and the variable x using the operations of addition, subtraction, multiplication, division and exponentiation with a natural exponent.
If r(x) is a rational expression, then the equation r(x) = 0 is called a rational equation.
However, in practice it is more convenient to use a slightly broader interpretation of the term “rational equation”: this is an equation of the form h(x) = q(x), where h(x) and q(x) are rational expressions.
Until now, we could not solve any rational equation, but only one that, as a result of various transformations and reasoning, was reduced to linear equation. Now our capabilities are much greater: we will be able to solve a rational equation that reduces not only to linear
mu, but also to the quadratic equation.
Let us recall how we solved rational equations before and try to formulate a solution algorithm.
Example 1. Solve the equation
Solution. Let's rewrite the equation in the form
In this case, as usual, we take advantage of the fact that the equalities A = B and A - B = 0 express the same relationship between A and B. This allowed us to move the term to the left side of the equation with the opposite sign.
Let's transform the left side of the equation. We have
Let us recall the conditions of equality fractions zero: if and only if two relations are simultaneously satisfied:
1) the numerator of the fraction is zero (a = 0); 2) the denominator of the fraction is different from zero).
Equating the numerator of the fraction on the left side of equation (1) to zero, we obtain
It remains to check the fulfillment of the second condition indicated above. The relation means for equation (1) that . The values x 1 = 2 and x 2 = 0.6 satisfy the indicated relationships and therefore serve as the roots of equation (1), and at the same time the roots of the given equation.
1) Let's transform the equation to the form
2) Let us transform the left side of this equation:
(simultaneously changed the signs in the numerator and
fractions).
Thus, given equation takes the form
3) Solve the equation x 2 - 6x + 8 = 0. Find
4) For the found values, check the fulfillment of the condition 
. The number 4 satisfies this condition, but the number 2 does not. This means that 4 is the root of the given equation, and 2 is an extraneous root.
ANSWER: 4.
2. Solving rational equations by introducing a new variable
The method of introducing a new variable is familiar to you; we have used it more than once. Let us show with examples how it is used in solving rational equations.
Example 3. Solve the equation x 4 + x 2 - 20 = 0.
Solution. Let's introduce a new variable y = x 2 . Since x 4 = (x 2) 2 = y 2, the given equation can be rewritten as
y 2 + y - 20 = 0.
This is a quadratic equation, the roots of which can be found using known formulas; we get y 1 = 4, y 2 = - 5.
But y = x 2, which means the problem has been reduced to solving two equations:
x 2 =4; x 2 = -5.
From the first equation we find that the second equation has no roots.
Answer: .
An equation of the form ax 4 + bx 2 + c = 0 is called a biquadratic equation (“bi” is two, i.e., a kind of “double quadratic” equation). The equation just solved was precisely biquadratic. Any biquadratic equation is solved in the same way as the equation from Example 3: introduce a new variable y = x 2, solve the resulting quadratic equation with respect to the variable y, and then return to the variable x.
Example 4. Solve the equation
Solution. Note that the same expression x 2 + 3x appears twice here. This means that it makes sense to introduce a new variable y = x 2 + 3x. This will allow you to rewrite the equation in a simpler and looking nice(which, in fact, is the purpose of introducing a new variable- and simplifying the recording
becomes clearer, and the structure of the equation becomes clearer):
Now let’s use the algorithm for solving a rational equation.
1) Let’s move all the terms of the equation into one part:
= 0
2) Transform the left side of the equation
So, we have transformed the given equation to the form
3) From the equation - 7y 2 + 29y -4 = 0 we find (you and I have already solved quite a lot of quadratic equations, so it’s probably not worth always giving detailed calculations in the textbook).
4) Let's check the found roots using condition 5 (y - 3) (y + 1). Both roots satisfy this condition.
So, the quadratic equation for the new variable y is solved: 
Since y = x 2 + 3x, and y, as we have established, takes two values: 4 and , we still have to solve two equations: x 2 + 3x = 4; x 2 + Zx = . The roots of the first equation are the numbers 1 and - 4, the roots of the second equation are the numbers
In the examples considered, the method of introducing a new variable was, as mathematicians like to say, adequate to the situation, that is, it corresponded well to it. Why? Yes, because the same expression clearly appeared in the equation several times and there was a reason to designate this expression new letter. But this does not always happen; sometimes a new variable “appears” only during the transformation process. This is exactly what will happen in the next example.
Example 5. Solve the equation
x(x-1)(x-2)(x-3) = 24.
Solution. We have
x(x - 3) = x 2 - 3x;
(x - 1)(x - 2) = x 2 -Зx+2.
This means that the given equation can be rewritten in the form
(x 2 - 3x)(x 2 + 3x + 2) = 24
Now a new variable has “appeared”: y = x 2 - 3x.
With its help, the equation can be rewritten in the form y (y + 2) = 24 and then y 2 + 2y - 24 = 0. The roots of this equation are the numbers 4 and -6.
Returning to the original variable x, we obtain two equations x 2 - 3x = 4 and x 2 - 3x = - 6. From the first equation we find x 1 = 4, x 2 = - 1; the second equation has no roots.
ANSWER: 4, - 1.
In this article I will show you algorithms for solving seven types of rational equations, which can be reduced to quadratic by changing variables. In most cases, the transformations that lead to replacement are very non-trivial, and it is quite difficult to guess about them on your own.
For each type of equation, I will explain how to make a change of variable in it, and then show a detailed solution in the corresponding video tutorial.
You have the opportunity to continue solving the equations yourself, and then check your solution with the video lesson.
So, let's begin.
1 . (x-1)(x-7)(x-4)(x+2)=40
Note that on the left side of the equation there is a product of four brackets, and on the right side there is a number.
1. Let's group the brackets by two so that the sum of the free terms is the same.
2. Multiply them.
3. Let's introduce a change of variable.
In our equation, we will group the first bracket with the third, and the second with the fourth, since (-1)+(-4)=(-7)+2:
At this point the variable replacement becomes obvious:
We get the equation 
Answer: 
2 .
An equation of this type is similar to the previous one with one difference: on the right side of the equation is the product of the number and . And it is solved in a completely different way:
1. We group the brackets by two so that the product of the free terms is the same.
2. Multiply each pair of brackets.
3. We take x out of each factor.
4. Divide both sides of the equation by .
5. We introduce a change of variable.
In this equation, we group the first bracket with the fourth, and the second with the third, since:
Note that in each bracket the coefficient at and the free term are the same. Let's take a factor out of each bracket:
Since x=0 is not a root of the original equation, we divide both sides of the equation by . We get:
We get the equation: 
Answer: 
3
. 
Note that the denominators of both fractions are square trinomials, for which the leading coefficient and the free term are the same. Let us take x out of the bracket, as in the equation of the second type. We get:
Divide the numerator and denominator of each fraction by x:
Now we can introduce a variable replacement:
We obtain an equation for the variable t:
4 .
Note that the coefficients of the equation are symmetrical with respect to the central one. This equation is called returnable .
To solve it,
1. Divide both sides of the equation by (We can do this since x=0 is not a root of the equation.) We get:
2. Let’s group the terms in this way:
3. In each group, let’s take the common factor out of brackets:
4. Let's introduce the replacement:
5. Express through t the expression:
From here 
We get the equation for t:
Answer:
5. Homogeneous equations.
Equations that have a homogeneous structure can be encountered when solving exponential, logarithmic and trigonometric equations, so you need to be able to recognize it.
Homogeneous equations have the following structure:
In this equality, A, B and C are numbers, and the square and circle denote identical expressions. That is, on the left side of a homogeneous equation there is a sum of monomials having the same degree (in in this case the degree of the monomials is 2), and there is no free term.
To solve a homogeneous equation, divide both sides by
Attention! When dividing the right and left sides of an equation by an expression containing an unknown, you can lose roots. Therefore, it is necessary to check whether the roots of the expression by which we divide both sides of the equation are the roots of the original equation.
Let's go the first way. We get the equation:
Now we introduce variable replacement:
Let us simplify the expression and obtain a biquadratic equation for t:
Answer: or
7
. 
This equation has the following structure:
To solve it, you need to select a complete square on the left side of the equation.
To select a full square, you need to add or subtract twice the product. Then we get the square of the sum or difference. This is crucial for successful variable replacement.
Let's start by finding twice the product. This will be the key to replacing the variable. In our equation, twice the product is equal to
Now let's figure out what is more convenient for us to have - the square of the sum or the difference. Let's first consider the sum of expressions:
Great! This expression is exactly equal to twice the product. Then, in order to get the square of the sum in brackets, you need to add and subtract the double product:
