Angle ABC is an inscribed angle. It rests on the arc AC, enclosed between its sides (Fig. 330).

Theorem. An inscribed angle is measured by the half of the arc on which it subtends.

This should be understood this way: an inscribed angle contains as many angular degrees, minutes and seconds as there are arc degrees, minutes and seconds contained in the half of the arc on which it rests.

When proving this theorem, three cases must be considered.

First case. The center of the circle lies on the side of the inscribed angle (Fig. 331).

Let ∠ABC be an inscribed angle and the center of the circle O lies on side BC. It is required to prove that it is measured by half an arc AC.

Let's connect point A to the center of the circle. We obtain an isosceles \(\Delta\)AOB, in which AO = OB, as the radii of the same circle. Therefore, ∠A = ∠B.

∠AOC is external to triangle AOB, so ∠AOC = ∠A + ∠B, and since angles A and B are equal, then ∠B is 1/2 ∠AOC.

But ∠AOC is measured by arc AC, therefore ∠B is measured by half of arc AC.

For example, if \(\breve(AC)\) contains 60°18', then ∠B contains 30°9'.

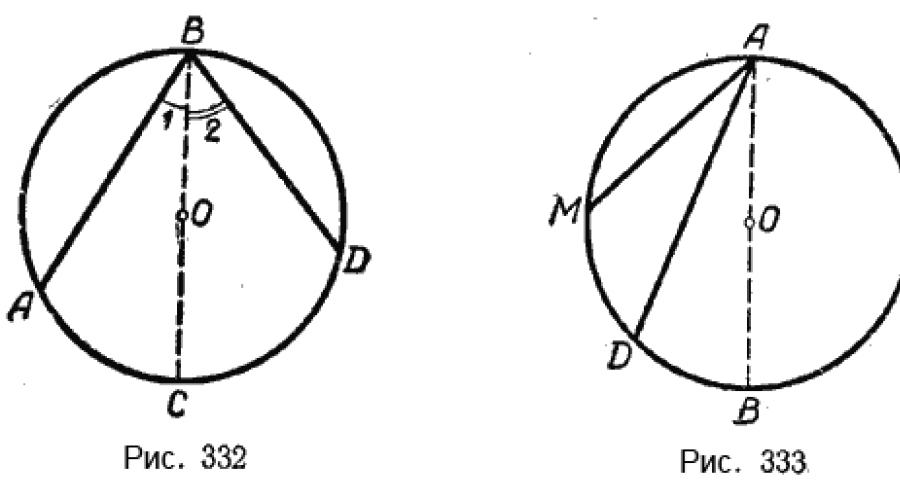
Second case. The center of the circle lies between the sides of the inscribed angle (Fig. 332).

Let ∠ABD be an inscribed angle. The center of circle O lies between its sides. We need to prove that ∠ABD is measured by half the arc AD.

To prove this, let us draw the diameter BC. Angle ABD is split into two angles: ∠1 and ∠2.

∠1 is measured by half an arc AC, and ∠2 is measured by half an arc CD, therefore, the entire ∠ABD is measured by 1 / 2 \(\breve(AC)\) + 1 / 2 \(\breve(CD)\), i.e. . half arc AD.

For example, if \(\breve(AD)\) contains 124°, then ∠B contains 62°.

Third case. The center of the circle lies outside the inscribed angle (Fig. 333).

Let ∠MAD be an inscribed angle. The center of circle O is outside the corner. We need to prove that ∠MAD is measured by half the arc MD.

To prove this, let's draw the diameter AB. ∠MAD = ∠MAB - ∠DAB. But ∠MAB measures 1 / 2 \(\breve(MB)\), and ∠DAB measures 1 / 2 \(\breve(DB)\).

Therefore, ∠MAD measures 1 / 2 (\(\breve(MB) - \breve(DB))\), i.e. 1 / 2 \(\breve(MD)\).

For example, if \(\breve(MD)\) contains 48° 38", then ∠MAD contains 24° 19' 8".

Consequences
1. All inscribed angles subtending the same arc are equal to each other, since they are measured by half of the same arc (Fig. 334, a).

2. An inscribed angle subtended by a diameter is a right angle, since it subtends half a circle. Half a circle contains 180 arc degrees, which means that the angle based on the diameter contains 90 arc degrees (Fig. 334, b).

The concept of inscribed and central angle

Let us first introduce the concept of a central angle.

Note 1

Note that the degree measure of a central angle is equal to the degree measure of the arc on which it rests.

Let us now introduce the concept of an inscribed angle.

Definition 2

An angle whose vertex lies on a circle and whose sides intersect the same circle is called an inscribed angle (Fig. 2).

Figure 2. Inscribed angle

Inscribed angle theorem

Theorem 1

The degree measure of an inscribed angle is equal to half the degree measure of the arc on which it rests.

Proof.

Let us be given a circle with center at point $O$. Let's denote the inscribed angle $ACB$ (Fig. 2). The following three cases are possible:

• Ray $CO$ coincides with any side of the angle. Let this be the side $CB$ (Fig. 3).

Figure 3.

In this case, the arc $AB$ is less than $(180)^(()^\circ )$, therefore, central angle$AOB$ is equal to arc $AB$. Since $AO=OC=r$, then the triangle $AOC$ is isosceles. This means that the base angles $CAO$ and $ACO$ are equal to each other. According to the theorem on the external angle of a triangle, we have:

• Beam $CO$ divides internal corner at two angles. Let it intersect the circle at point $D$ (Fig. 4).

Figure 4.

We get

• Ray $CO$ does not divide the interior angle into two angles and does not coincide with any of its sides (Fig. 5).

Figure 5.

Let us consider angles $ACD$ and $DCB$ separately. According to what was proved in point 1, we get

We get

The theorem is proven.

Let's give consequences from this theorem.

Corollary 1: Inscribed angles that rest on the same arc are equal to each other.

Corollary 2: An inscribed angle that subtends a diameter is a right angle.

Instructions

If the radius (R) of the circle and the length of the arc (L) corresponding to the desired central angle (θ) are known, it can be calculated both in degrees and in radians. The total is determined by the formula 2*π*R and corresponds to a central angle of 360° or two Pi numbers, if radians are used instead of degrees. Therefore, proceed from the proportion 2*π*R/L = 360°/θ = 2*π/θ. Express from it the central angle in radians θ = 2*π/(2*π*R/L) = L/R or degrees θ = 360°/(2*π*R/L) = 180*L/(π* R) and calculate using the resulting formula.

Based on the length of the chord (m) connecting the points that determine the central angle (θ), its value can also be calculated if the radius (R) of the circle is known. To do this, consider a triangle formed by two radii and . This isosceles triangle, everyone is known, but you need to find the angle opposite the base. Sine of its half equal to the ratio the length of the base - the chord - to twice the length of the side - the radius. Therefore, use the inverse sine function for calculations - arcsine: θ = 2*arcsin(½*m/R).

The central angle can be specified in fractions of a revolution or from a rotated angle. For example, if you need to find the central angle corresponding to a quarter of a full revolution, divide 360° by four: θ = 360°/4 = 90°. The same value in radians should be 2*π/4 ≈ 3.14/2 ≈ 1.57. The unfolded angle is equal to half a full revolution, therefore, for example, the central angle corresponding to a quarter of it will be half the values ​​​​calculated above in both degrees and radians.

The inverse of sine is called a trigonometric function arcsine. It can take values ​​within half the number Pi, both positive and negative. negative side when measured in radians. When measured in degrees, these values ​​will be respectively in the range from -90° to +90°.

Instructions

Some “round” values ​​do not need to be calculated; they are easier to remember. For example: - if the function argument is zero, then the arcsine of it is also zero; - of 1/2 is equal to 30° or 1/6 Pi, if measured; - arcsine of -1/2 is -30° or -1/ 6 from the number Pi in; - the arcsine of 1 is equal to 90° or 1/2 of the number Pi in radians; - the arcsine of -1 is equal to -90° or -1/2 of the number Pi in radians;

To measure the values ​​of this function from other arguments, the easiest way is to use a standard Windows calculator, if you have one at hand. To start, open the main menu on the “Start” button (or by pressing the WIN key), go to the “All Programs” section, and then to the “Accessories” subsection and click “Calculator”.

Switch the calculator interface to the operating mode that allows you to calculate trigonometric functions. To do this, open the “View” section in its menu and select “Engineering” or “Scientific” (depending on the type of operating system).

Enter the value of the argument from which the arctangent should be calculated. This can be done by clicking the buttons on the calculator interface with the mouse, or by pressing the keys on , or by copying the value (CTRL + C) and then pasting it (CTRL + V) into the input field of the calculator.

Select the units of measurement in which you need to obtain the result of the function calculation. Below the input field there are three options, from which you need to select (by clicking it with the mouse) one - , radians or rads.

Check the checkbox that inverts the functions indicated on the calculator interface buttons. Next to it is a short inscription Inv.

Click the sin button. The calculator will invert the function associated with it, perform the calculation and present you with the result in the specified units.

Video on the topic

One of the common geometric problems is calculating the area of ​​a circular segment - the part of the circle bounded by a chord and the corresponding chord by an arc of a circle.

The area of ​​a circular segment is equal to the difference between the area of ​​the corresponding circular sector and the area of ​​the triangle formed by the radii of the sector corresponding to the segment and the chord limiting the segment.

Example 1

The length of the chord subtending the circle is equal to the value a. The degree measure of the arc corresponding to the chord is 60°. Find the area of ​​the circular segment.

Solution

A triangle formed by two radii and a chord is isosceles, so the altitude drawn from the vertex of the central angle to the side of the triangle formed by the chord will also be the bisector of the central angle, dividing it in half, and the median, dividing the chord in half. Knowing that the sine of the angle is equal to the ratio of the opposite leg to the hypotenuse, we can calculate the radius:

Sin 30°= a/2:R = 1/2;

Sc = πR²/360°*60° = πa²/6

S▲=1/2*ah, where h is the height drawn from the vertex of the central angle to the chord. According to the Pythagorean theorem h=√(R²-a²/4)= √3*a/2.

Accordingly, S▲=√3/4*a².

The area of ​​the segment, calculated as Sreg = Sc - S▲, is equal to:

Sreg = πa²/6 - √3/4*a²

By substituting a numerical value for the value of a, you can easily calculate the numerical value of the segment area.

Example 2

The radius of the circle is equal to a. The degree measure of the arc corresponding to the segment is 60°. Find the area of ​​the circular segment.

Solution:

The area of ​​the sector corresponding to a given angle can be calculated using the following formula:

Sc = πа²/360°*60° = πa²/6,

The area of ​​the triangle corresponding to the sector is calculated as follows:

S▲=1/2*ah, where h is the height drawn from the vertex of the central angle to the chord. By the Pythagorean theorem h=√(a²-a²/4)= √3*a/2.

Accordingly, S▲=√3/4*a².

And finally, the area of ​​the segment, calculated as Sreg = Sc - S▲, is equal to:

Sreg = πa²/6 - √3/4*a².

The solutions in both cases are almost identical. Thus, we can conclude that to calculate the area of ​​a segment in the simplest case, it is enough to know the value of the angle corresponding to the arc of the segment and one of two parameters - either the radius of the circle or the length of the chord subtending the arc of the circle forming the segment.

Sources:

• Segment - geometry

Average level

Circle and inscribed angle. Visual guide (2019)

Basic terms.

How well do you remember all the names associated with the circle? Just in case, let us remind you - look at the pictures - refresh your knowledge.

Firstly - The center of a circle is a point from which the distances from all points on the circle are the same.

Secondly - radius - a line segment connecting the center and a point on the circle.

There are a lot of radii (as many as there are points on the circle), but All radii have the same length.

Sometimes for short radius they call it exactly length of the segment“the center is a point on the circle,” and not the segment itself.

And here's what happens if you connect two points on a circle? Also a segment?

So, this segment is called "chord".

Just as in the case of radius, diameter is often the length of a segment connecting two points on a circle and passing through the center. By the way, how are diameter and radius related? Look carefully. Of course, the radius is equal to half the diameter.

In addition to chords, there are also secants.

Remember the simplest thing?

Central angle is the angle between two radii.

And now - the inscribed angle

Inscribed angle - the angle between two chords that intersect at a point on a circle.

In this case, they say that the inscribed angle rests on an arc (or on a chord).

Look at the picture:

Measurements of arcs and angles.

Circumference. Arcs and angles are measured in degrees and radians. First, about degrees. There are no problems for angles - you need to learn how to measure the arc in degrees.

The degree measure (arc size) is the value (in degrees) of the corresponding central angle

What does the word “appropriate” mean here? Let's look carefully:

Do you see two arcs and two central angles? Well, a larger arc corresponds to a larger angle (and it’s okay that it’s larger), and a smaller arc corresponds to a smaller angle.

So, we agreed: the arc contains the same number of degrees as the corresponding central angle.

And now about the scary thing - about radians!

What kind of beast is this “radian”?

Imagine this: Radians are a way of measuring angles... in radii!

An angle of radians is a central angle whose arc length is equal to the radius of the circle.

Then the question arises - how many radians are there in a straight angle?

In other words: how many radii “fit” in half a circle? Or in another way: how many times is the length of half a circle greater than the radius?

Scientists asked this question back in Ancient Greece.

And so, after a long search, they discovered that the ratio of the circumference to the radius does not want to be expressed in “human” numbers like, etc.

And it’s not even possible to express this attitude through roots. That is, it turns out that it is impossible to say that half a circle is times or times larger than the radius! Can you imagine how amazing it was for people to discover this for the first time?! For the ratio of the length of half a circle to the radius, “normal” numbers were not enough. I had to enter a letter.

So, - this is a number expressing the ratio of the length of the semicircle to the radius.

Now we can answer the question: how many radians are there in a straight angle? It contains radians. Precisely because half the circle is times larger than the radius.

Ancient (and not so ancient) people throughout the centuries (!) tried to more accurately calculate this mysterious number, to better express it (at least approximately) through “ordinary” numbers. And now we are incredibly lazy - two signs after a busy day are enough for us, we are used to

Think about it, this means, for example, that the length of a circle with a radius of one is approximately equal, but this exact length is simply impossible to write down with a “human” number - you need a letter. And then this circumference will be equal. And of course, the circumference of the radius is equal.

Let's go back to radians.

We have already found out that a straight angle contains radians.

What we have:

That means I'm glad, that is, I'm glad. In the same way, a plate with the most popular angles is obtained.

The relationship between the values ​​of the inscribed and central angles.

There is an amazing fact:

The inscribed angle is half the size of the corresponding central angle.

Look how this statement looks in the picture. A “corresponding” central angle is one whose ends coincide with the ends of the inscribed angle, and the vertex is at the center. And at the same time, the “corresponding” central angle must “look” at the same chord () as the inscribed angle.

Why is this so? Let's look at a simple case first. Let one of the chords pass through the center. It happens like that sometimes, right?

What happens here? Let's consider. It is isosceles - after all, and - radii. So, (labeled them).

Now let's look at. This is the outer corner for! We recall that an external angle is equal to the sum of two internal angles not adjacent to it, and write:

That is! Unexpected effect. But there is also a central angle for the inscribed.

This means that for this case they proved that the central angle is twice the inscribed angle. But it hurts too much special case: Isn’t it true that the chord doesn’t always go straight through the center? But it’s okay, now this particular case will help us a lot. Look: second case: let the center lie inside.

Let's do this: draw the diameter. And then... we see two pictures that were already analyzed in the first case. Therefore we already have that

This means (in the drawing, a)

Well, that leaves the last case: the center is outside the corner.

We do the same thing: draw the diameter through the point. Everything is the same, but instead of a sum there is a difference.

That's all!

Let's now form two main and very important consequences from the statement that the inscribed angle is half the central angle.

Corollary 1

All inscribed angles based on one arc are equal to each other.

We illustrate:

There are countless inscribed angles based on the same arc (we have this arc), they may look completely different, but they all have the same central angle (), which means that all these inscribed angles are equal between themselves.

Corollary 2

The angle subtended by the diameter is a right angle.

Look: what angle is central to?

Certainly, . But he is equal! Well, therefore (as well as many more inscribed angles resting on) and is equal.

Angle between two chords and secants

But what if the angle we are interested in is NOT inscribed and NOT central, but, for example, like this:

or like this?

Is it possible to somehow express it through some central angles? It turns out that it is possible. Look: we are interested.

a) (as an external corner for). But - inscribed, rests on the arc -. - inscribed, rests on the arc - .

For beauty they say:

The angle between the chords is equal to half the sum angular values arcs enclosed in this angle.

They write this for brevity, but of course, when using this formula you need to keep in mind the central angles

b) And now - “outside”! How to be? Yes, almost the same! Only now (we apply the property again external corner For). That is now.

And that means... Let’s bring beauty and brevity to the notes and wording:

The angle between the secants is equal to half the difference in the angular values ​​of the arcs enclosed in this angle.

Well, now you are armed with all the basic knowledge about angles related to a circle. Go ahead, take on the challenges!

CIRCLE AND INSINALED ANGLE. AVERAGE LEVEL

Even a five-year-old child knows what a circle is, right? Mathematicians, as always, have an abstruse definition on this subject, but we will not give it (see), but rather let us remember what the points, lines and angles associated with a circle are called.

Important Terms

Firstly:

Secondly:

There is another accepted expression: “the chord contracts the arc.” Here in the figure, for example, the chord subtends the arc. And if a chord suddenly passes through the center, then it has a special name: “diameter”.

By the way, how are diameter and radius related? Look carefully. Of course,

And now - the names for the corners.

Natural, isn't it? The sides of the angle extend from the center - which means the angle is central.

This is where difficulties sometimes arise. Pay attention - NOT ANY angle inside a circle is inscribed, but only one whose vertex “sits” on the circle itself.

Let's see the difference in the pictures:

Another way they say:

There is one tricky point here. What is the “corresponding” or “own” central angle? Just an angle with the vertex at the center of the circle and the ends at the ends of the arc? Not certainly in that way. Look at the drawing.

One of them, however, doesn’t even look like a corner - it’s bigger. But a triangle cannot have more angles, but a circle may well! So: the smaller arc AB corresponds to a smaller angle (orange), and the larger arc corresponds to a larger one. Just like that, isn't it?

The relationship between the magnitudes of the inscribed and central angles

Remember this very important statement:

In textbooks they like to write this same fact like this:

Isn’t it true that the formulation is simpler with a central angle?

But still, let’s find a correspondence between the two formulations, and at the same time learn to find in the drawings the “corresponding” central angle and the arc on which the inscribed angle “rests”.

Look: here is a circle and an inscribed angle:

Where is its “corresponding” central angle?

Let's look again:

What is the rule?

But! In this case, it is important that the inscribed and central angles “look” at the arc from one side. For example:

Oddly enough, blue! Because the arc is long, longer than half the circle! So don’t ever get confused!

What consequence can be deduced from the “halfness” of the inscribed angle?

But, for example:

Angle subtended by diameter

Have you already noticed that mathematicians love to talk about the same thing in different words? Why do they need this? You see, the language of mathematics, although formal, is alive, and therefore, as in ordinary language, every time you want to say it in a way that is more convenient. Well, we have already seen what “an angle rests on an arc” means. And imagine, the same picture is called “an angle rests on a chord.” On what? Yes, of course, to the one that tightens this arc!

When is it more convenient to lean on a chord than on an arc?

Well, in particular, when this chord is a diameter.

There is a surprisingly simple, beautiful and useful statement for such a situation!

Look: here is the circle, the diameter and the angle that rests on it.

CIRCLE AND INSINALED ANGLE. BRIEFLY ABOUT THE MAIN THINGS

1. Basic concepts.

3. Measurements of arcs and angles.

An angle of radians is a central angle whose arc length is equal to the radius of the circle.

This is a number that expresses the ratio of the length of a semicircle to its radius.

The circumference of the radius is equal to.

4. The relationship between the values ​​of the inscribed and central angles.

Central angle- is the angle formed by two radii circle. An example of a central angle is angle AOB, BOC, COE, and so on.

ABOUT central corner And arc concluded between its parties are said to correspond each other.

1. if central angles arcs are equal.

2. if central angles are not equal, then the greater of them corresponds to the greater arc.

Let AOB and COD be two central angles, equal or unequal. Let's rotate the sector AOB around the center in the direction indicated by the arrow, so that the radius OA coincides with OC. Then, if the central angles are equal, then the radius OA will coincide with OD and the arc AB with the arc CD.

This means that these arcs will be equal.

If central angles are not equal, then the radius OB will not go along OD, but in some other direction, for example, along OE or OF. In both cases, a larger angle obviously corresponds to a larger arc.

The theorem we proved for one circle remains true for equal circles, because such circles do not differ from each other in anything except their position.

Reverse offers will also be true . In one circle or in equal circles:

1. if arcs are equal, then their corresponding central angles are equal.

2. if arcs are not equal, then the greater of them corresponds to the greater central angle.

In one circle or in equal circles, central angles are related as their corresponding arcs. Or paraphrasing we get that the central angle proportional the arc corresponding to it.