What is cosine alpha equal to? Formulas for double angles and addition of arguments. Graph of the cotangent function, y = ctg x
Read also
Centered at point A.
α is the angle expressed in radians.
Tangent ( tan α) is a trigonometric function depending on the angle α between the hypotenuse and the leg right triangle, equal to the ratio length of the opposite side |BC| to the length of the adjacent leg |AB| .
Cotangent ( ctg α) is a trigonometric function depending on the angle α between the hypotenuse and the leg of a right triangle, equal to the ratio of the length of the adjacent leg |AB| to the length of the opposite leg |BC| .
Tangent
Where n- whole.
In Western literature, tangent is denoted as follows:
.
;
;
.
Graph of the tangent function, y = tan x
Cotangent
Where n- whole.
In Western literature, cotangent is denoted as follows:
.
The following notations are also accepted:
;
;
.
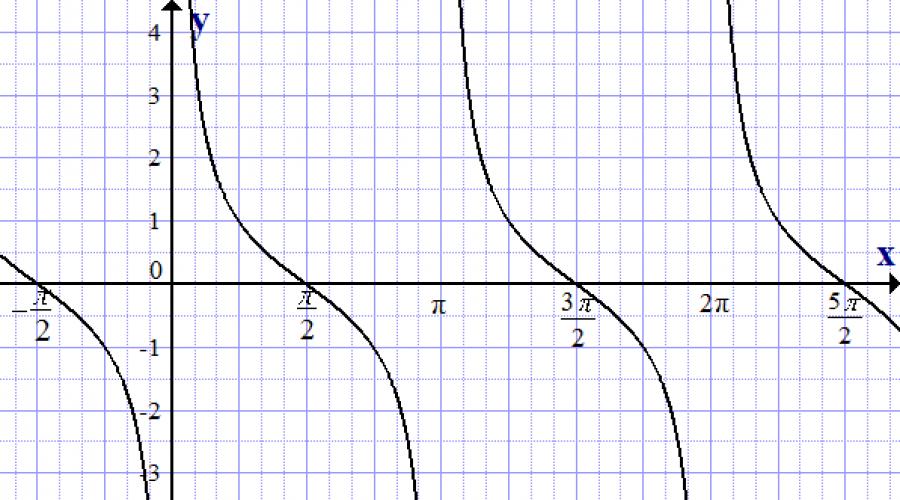
Graph of the cotangent function, y = ctg x

Properties of tangent and cotangent
Periodicity
Functions y = tg x and y = ctg x are periodic with period π.
Parity
The tangent and cotangent functions are odd.
Areas of definition and values, increasing, decreasing
The tangent and cotangent functions are continuous in their domain of definition (see proof of continuity). The main properties of tangent and cotangent are presented in the table ( n- whole).
| y= tg x | y= ctg x | |
| Scope and continuity | ||
| Range of values | -∞ < y < +∞ | -∞ < y < +∞ |
| Increasing | - | |
| Descending | - | |
| Extremes | - | - |
| Zeros, y = 0 | ||
| Intercept points with the ordinate axis, x = 0 | y= 0 | - |
Formulas
Expressions using sine and cosine
;
;
;
;
;
Formulas for tangent and cotangent from sum and difference
The remaining formulas are easy to obtain, for example
Product of tangents
Formula for the sum and difference of tangents
This table presents the values of tangents and cotangents for certain values of the argument. 
Expressions using complex numbers
Expressions through hyperbolic functions
;
;
Derivatives
; .
.
Derivative of the nth order with respect to the variable x of the function:
.
Deriving formulas for tangent > > > ; for cotangent > > >
Integrals
Series expansions
To obtain the expansion of the tangent in powers of x, you need to take several terms of the expansion in power series for functions sin x And cos x and divide these polynomials by each other, . This produces the following formulas.
At .
at .
Where Bn- Bernoulli numbers. They are determined either from the recurrence relation:
;
;
Where .
Or according to Laplace's formula: 
Inverse functions
The inverse functions of tangent and cotangent are arctangent and arccotangent, respectively.
Arctangent, arctg
, Where n- whole.
Arccotangent, arcctg
, Where n- whole.
References:
I.N. Bronstein, K.A. Semendyaev, Handbook of mathematics for engineers and college students, “Lan”, 2009.
G. Korn, Handbook of Mathematics for scientific workers and engineers, 2012.
- 2. Range of values: [-1;1]
- 3. Odd function.
- 7. Intervals on which the function is positive: (2*pi*n; pi+2*pi*n)
- 8. Intervals on which the function is negative: (-pi + 2*pi*n; 2*pi*n)
- 9. Increasing intervals: [-pi/2 +2*pi*n; pi/2 +2*pi*n]
- 10. Decreasing intervals:
- 11. Minimum points: -pi/2 +2*pi*n
- 12. Minimum function: -1
- 13. Maximum points: pi/2 +2*pi*n
- 14. Maximum function: 1
Properties of cosine
.jpg)
- 1. Definition area: entire number axis
- 2. Range of values: [-1;1]
- 3. Even function.
- 4. Smallest positive period: 2*pi
- 5. Coordinates of the points of intersection of the function graph with the Ox axis: (pi/2 +pi*n; 0)
- 6. Coordinates of the points of intersection of the function graph with the Oy axis: (0;1)
- 7. Intervals at which the function is positive: (-pi/2 +2*pi*n; pi/2 +2*pi*n)
- 8. Intervals at which the function is negative: (pi/2 +2*pi*n; 3*pi/2 +2*pi*n)
- 9. Increasing intervals: [-pi + 2*pi*n; 2*pi*n]
- 10. Decreasing intervals:
- 11. Minimum points: pi+2*pi*n
- 12. Minimum function: -1
- 13. Maximum points: 2*pi*n
- 14. Maximum function: 1
Properties of tangent
.jpg)
- 1. Definition area: (-pi/2 +pi*n; pi/2 +pi*n)
- 3. Odd function.
- 5. Coordinates of the points of intersection of the function graph with the Ox axis: (pi*n; 0)
- 6. Coordinates of the points of intersection of the function graph with the Oy axis: (0;0)
- 9. The function increases on intervals (-pi/2 + pi*n; pi/2 + pi*n)
Properties of cotangent
.jpg)
- 1. Domain: (pi*n; pi +pi*n)
- 2. Value range: entire number axis
- 3. Odd function.
- 4. Smallest positive period: pi
- 5. Coordinates of the points of intersection of the function graph with the Ox axis: (pi/2 + pi*n; 0)
- 6. Coordinates of the points of intersection of the function graph with the Oy axis: no
- 7. Intervals on which the function is positive: (pi*n; pi/2 +pi*n)
- 8. Intervals on which the function is negative: (-pi/2 +pi*n; pi*n)
- 9. The function decreases on intervals (pi*n; pi +pi*n)
- 10. There are no maximum and minimum points.
The figure below shows several unit circles, which indicate the signs of sine, cosine, tangent and cotangent in various coordinate quarters.
Sine and cosine originally arose from the need to calculate quantities in right triangles. It was noticed that if the degree measure of the angles in a right triangle is not changed, then the aspect ratio, no matter how much these sides change in length, always remains the same.
This is how the concepts of sine and cosine were introduced. The sine of an acute angle in a right triangle is the ratio of the opposite side to the hypotenuse, and the cosine is the ratio of the side adjacent to the hypotenuse.
Theorems of cosines and sines
But cosines and sines can be used for more than just right triangles. To find the value of an obtuse or acute angle or side of any triangle, it is enough to apply the theorem of cosines and sines.
The cosine theorem is quite simple: “The square of a side of a triangle is equal to the sum of the squares of the other two sides minus twice the product of those sides and the cosine of the angle between them.”
There are two interpretations of the sine theorem: small and extended. According to the minor: “In a triangle, the angles are proportional to the opposite sides.” This theorem is often expanded due to the property of the circumscribed circle of a triangle: “In a triangle, the angles are proportional to the opposite sides, and their ratio is equal to the diameter of the circumscribed circle.”
Derivatives
The derivative is a mathematical tool that shows how quickly a function changes relative to a change in its argument. Derivatives are used in geometry, and in a number of technical disciplines.
When solving problems you need to know table values derivatives trigonometric functions: sine and cosine. The derivative of a sine is a cosine, and a cosine is a sine, but with a minus sign.
Application in mathematics
Sines and cosines are especially often used in solving right triangles and problems related to them.
The convenience of sines and cosines is also reflected in technology. Angles and sides were easy to evaluate using the cosine and sine theorems, breaking down complex shapes and objects into “simple” triangles. Engineers who often deal with calculations of aspect ratios and degree measures spent a lot of time and effort calculating the cosines and sines of non-tabular angles.
Then Bradis tables came to the rescue, containing thousands of values of sines, cosines, tangents and cotangents different angles. In Soviet times, some teachers forced their students to memorize pages of Bradis tables.
Radian - angular magnitude arcs, length equal to the radius or 57.295779513° degrees.
Degree (in geometry) - 1/360th part of a circle or 1/90th part of a right angle.
π = 3.141592653589793238462… (approximate value of Pi).
Cosine table for angles: 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, 180°, 210°, 225°, 240°, 270°, 300°, 315°, 330°, 360°.
| Angle x (in degrees) | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Angle x (in radians) | 0 | π/6 | π/4 | π/3 | π/2 | 2 x π/3 | 3 x π/4 | 5 x π/6 | π | 7 x π/6 | 5 x π/4 | 4 x π/3 | 3 x π/2 | 5 x π/3 | 7 x π/4 | 11 x π/6 | 2 x π |
| cos x | 1 | √3/2 (0,8660) | √2/2 (0,7071) | 1/2 (0,5) | 0 | -1/2 (-0,5) | -√2/2 (-0,7071) | -√3/2 (-0,8660) | -1 | -√3/2 (-0,8660) | -√2/2 (-0,7071) | -1/2 (-0,5) | 0 | 1/2 (0,5) | √2/2 (0,7071) | √3/2 (0,8660) | 1 |
Important notes!
1. If you see gobbledygook instead of formulas, clear your cache. How to do this in your browser is written here:
2. Before you start reading the article, pay attention to our navigator for the most useful resource For
Sine, cosine, tangent, cotangent
The concepts of sine (), cosine (), tangent (), cotangent () are inextricably linked with the concept of angle. In order to have a good understanding of these, at first glance, complex concepts (which cause a state of horror in many schoolchildren), and to make sure that “the devil is not as terrible as he is painted,” let’s start from the very beginning and understand the concept of an angle.
Angle concept: radian, degree
Let's look at the picture. The vector has “turned” relative to the point by a certain amount. So the measure of this rotation relative to the initial position will be corner.
What else do you need to know about the concept of angle? Well, of course, angle units!
Angle, in both geometry and trigonometry, can be measured in degrees and radians.
An angle of (one degree) is called central angle in a circle, based on a circular arc equal to part of the circle. Thus, the entire circle consists of “pieces” of circular arcs, or the angle described by the circle is equal.

That is, the figure above shows an angle equal to, that is, this angle rests on a circular arc the size of the circumference.
An angle in radians is the central angle in a circle subtended by a circular arc whose length is equal to the radius of the circle. Well, did you figure it out? If not, then let's figure it out from the drawing.

So, the figure shows an angle equal to a radian, that is, this angle rests on a circular arc, the length of which is equal to the radius of the circle (the length is equal to the length or radius equal to length arcs). Thus, the arc length is calculated by the formula:
Where is the central angle in radians.
Well, knowing this, can you answer how many radians are contained in the angle described by the circle? Yes, for this you need to remember the formula for circumference. Here she is:
Well, now let’s correlate these two formulas and find that the angle described by the circle is equal. That is, by correlating the value in degrees and radians, we get that. Respectively, . As you can see, unlike "degrees", the word "radian" is omitted, since the unit of measurement is usually clear from the context.
How many radians are there? That's right!
Got it? Then go ahead and fix it:
Having difficulties? Then look answers:
Right triangle: sine, cosine, tangent, cotangent of angle
So, we figured out the concept of an angle. But what is sine, cosine, tangent, and cotangent of an angle? Let's figure it out. To do this, a right triangle will help us.

What are the sides of a right triangle called? That's right, hypotenuse and legs: the hypotenuse is the side that lies opposite the right angle (in our example this is the side); legs are the two remaining sides and (those adjacent to right angle), and, if we consider the legs relative to the angle, then the leg is the adjacent leg, and the leg is the opposite. So, now let’s answer the question: what are sine, cosine, tangent and cotangent of an angle?
Sine of angle- this is the ratio of the opposite (distant) leg to the hypotenuse.
In our triangle.
Cosine of angle- this is the ratio of the adjacent (close) leg to the hypotenuse.
In our triangle.
Tangent of the angle- this is the ratio of the opposite (distant) side to the adjacent (close).
In our triangle.
Cotangent of angle- this is the ratio of the adjacent (close) leg to the opposite (far).
In our triangle.
These definitions are necessary remember! To make it easier to remember which leg to divide into what, you need to clearly understand that in tangent And cotangent only the legs sit, and the hypotenuse appears only in sinus And cosine. And then you can come up with a chain of associations. For example, this one:
Cosine→touch→touch→adjacent;
Cotangent→touch→touch→adjacent.
First of all, you need to remember that sine, cosine, tangent and cotangent as the ratios of the sides of a triangle do not depend on the lengths of these sides (at the same angle). Do not believe? Then make sure by looking at the picture:

Consider, for example, the cosine of an angle. By definition, from a triangle: , but we can calculate the cosine of an angle from a triangle: . You see, the lengths of the sides are different, but the value of the cosine of one angle is the same. Thus, the values of sine, cosine, tangent and cotangent depend solely on the magnitude of the angle.
If you understand the definitions, then go ahead and consolidate them!
For the triangle shown in the figure below, we find.

Well, did you get it? Then try it yourself: calculate the same for the angle.
Unit (trigonometric) circle
Understanding the concepts of degree and radian, we considered a circle with a radius equal to. Such a circle is called single. It will be very useful when studying trigonometry. Therefore, let's look at it in a little more detail.

As you can see, this circle is constructed in the Cartesian coordinate system. The radius of the circle is equal to one, while the center of the circle lies at the origin of coordinates, the initial position of the radius vector is fixed along the positive direction of the axis (in our example, this is the radius).
Each point on the circle corresponds to two numbers: the axis coordinate and the axis coordinate. What are these coordinate numbers? And in general, what do they have to do with the topic at hand? To do this, we need to remember about the considered right triangle. In the figure above, you can see two whole right triangles. Consider a triangle. It is rectangular because it is perpendicular to the axis.
What is the triangle equal to? That's right. In addition, we know that is the radius of the unit circle, which means . Let's substitute this value into our formula for cosine. Here's what happens:
What is the triangle equal to? Well, of course, ! Substitute the radius value into this formula and get:
So, can you tell what coordinates the point has, belonging to a circle? Well, no way? What if you realize that and are just numbers? Which coordinate does it correspond to? Well, of course, the coordinates! And what coordinate does it correspond to? That's right, coordinates! Thus, period.

What then are and equal to? That's right, let's use the corresponding definitions of tangent and cotangent and get that, a.
What if the angle is larger? For example, like in this picture:

What has changed in this example? Let's figure it out. To do this, let's turn again to a right triangle. Consider a right triangle: angle (as adjacent to an angle). What are the values of sine, cosine, tangent and cotangent for an angle? That's right, we adhere to the corresponding definitions of trigonometric functions:
Well, as you can see, the value of the sine of the angle still corresponds to the coordinate; the value of the cosine of the angle - the coordinate; and the values of tangent and cotangent to the corresponding ratios. Thus, these relations apply to any rotation of the radius vector.
It has already been mentioned that the initial position of the radius vector is along the positive direction of the axis. So far we have rotated this vector counterclockwise, but what happens if we rotate it clockwise? Nothing extraordinary, you will also get an angle of a certain value, but it will only be negative. Thus, when rotating the radius vector counterclockwise, we get positive angles, and when rotating clockwise - negative.
So, we know that a whole revolution of the radius vector around a circle is or. Is it possible to rotate the radius vector to or to? Well, of course you can! In the first case, therefore, the radius vector will make one full revolution and stop at position or.
In the second case, that is, the radius vector will make three full revolutions and stop at position or.
Thus, from the above examples we can conclude that angles that differ by or (where is any integer) correspond to the same position of the radius vector.
The figure below shows an angle. The same image corresponds to the corner, etc. This list can be continued indefinitely. All these angles can be written by the general formula or (where is any integer)

Now, knowing the definitions of the basic trigonometric functions and using the unit circle, try to answer what the values are:
Here's a unit circle to help you:

Having difficulties? Then let's figure it out. So we know that:
From here, we determine the coordinates of the points corresponding to certain angle measures. Well, let's start in order: the angle at corresponds to a point with coordinates, therefore:
Does not exist;
Further, adhering to the same logic, we find out that the corners in correspond to points with coordinates, respectively. Knowing this, it is easy to determine the values of trigonometric functions at the corresponding points. Try it yourself first, and then check the answers.
Answers:
Thus, we can make the following table:

There is no need to remember all these values. It is enough to remember the correspondence between the coordinates of points on the unit circle and the values of trigonometric functions:
But the values of the trigonometric functions of angles in and, given in the table below, must be remembered:

Don't be scared, now we'll show you one example quite simple to remember the corresponding values:
To use this method, it is vital to remember the values of the sine for all three measures of angle (), as well as the value of the tangent of the angle. Knowing these values, it is quite simple to restore the entire table - the cosine values are transferred in accordance with the arrows, that is:
Knowing this, you can restore the values for. The numerator " " will match and the denominator " " will match. Cotangent values are transferred in accordance with the arrows indicated in the figure. If you understand this and remember the diagram with the arrows, then it will be enough to remember all the values from the table.
Coordinates of a point on a circle
Is it possible to find a point (its coordinates) on a circle, knowing the coordinates of the center of the circle, its radius and angle of rotation?
Well, of course you can! Let's get it out general formula to find the coordinates of a point.
For example, here is a circle in front of us:

We are given that the point is the center of the circle. The radius of the circle is equal. It is necessary to find the coordinates of a point obtained by rotating the point by degrees.
As can be seen from the figure, the coordinate of the point corresponds to the length of the segment. The length of the segment corresponds to the coordinate of the center of the circle, that is, it is equal. The length of a segment can be expressed using the definition of cosine:
Then we have that for the point coordinate.
Using the same logic, we find the y coordinate value for the point. Thus,
So, in general view coordinates of points are determined by the formulas:
Coordinates of the center of the circle,
Circle radius,
The rotation angle of the vector radius.
As you can see, for the unit circle we are considering, these formulas are significantly reduced, since the coordinates of the center are equal to zero and the radius is equal to one:
Well, let's try out these formulas by practicing finding points on a circle?
1. Find the coordinates of a point on the unit circle obtained by rotating the point on.
2. Find the coordinates of a point on the unit circle obtained by rotating the point on.
3. Find the coordinates of a point on the unit circle obtained by rotating the point on.
4. The point is the center of the circle. The radius of the circle is equal. It is necessary to find the coordinates of the point obtained by rotating the initial radius vector by.
5. The point is the center of the circle. The radius of the circle is equal. It is necessary to find the coordinates of the point obtained by rotating the initial radius vector by.
Having trouble finding the coordinates of a point on a circle?
Solve these five examples (or get good at solving them) and you will learn to find them!
SUMMARY AND BASIC FORMULAS
The sine of an angle is the ratio of the opposite (far) leg to the hypotenuse.
The cosine of an angle is the ratio of the adjacent (close) leg to the hypotenuse.
The tangent of an angle is the ratio of the opposite (far) side to the adjacent (close) side.
The cotangent of an angle is the ratio of the adjacent (close) side to the opposite (far) side.
Well, the topic is over. If you are reading these lines, it means you are very cool.
Because only 5% of people are able to master something on their own. And if you read to the end, then you are in this 5%!
Now the most important thing.
You have understood the theory on this topic. And, I repeat, this... this is just super! You are already better than the vast majority of your peers.
The problem is that this may not be enough...
For what?
For successful completion Unified State Exam, for admission to college on a budget and, MOST IMPORTANTLY, for life.
I won’t convince you of anything, I’ll just say one thing...
People who received a good education, earn much more than those who did not receive it. This is statistics.
But this is not the main thing.
The main thing is that they are MORE HAPPY (there are such studies). Perhaps because there is much more open before them more possibilities and life becomes brighter? Don't know...
But think for yourself...
What does it take to be sure to be better than others on the Unified State Exam and ultimately be... happier?
GAIN YOUR HAND BY SOLVING PROBLEMS ON THIS TOPIC.
You won't be asked for theory during the exam.
You will need solve problems against time.
And, if you haven’t solved them (A LOT!), you’ll definitely make a stupid mistake somewhere or simply won’t have time.
It's like in sports - you need to repeat it many times to win for sure.
Find the collection wherever you want, necessarily with solutions, detailed analysis and decide, decide, decide!
You can use our tasks (optional) and we, of course, recommend them.
In order to get better at using our tasks, you need to help extend the life of the YouClever textbook you are currently reading.
How? There are two options:
- Unlock all hidden tasks in this article -
- Unlock access to all hidden tasks in all 99 articles of the textbook - Buy a textbook - 499 RUR
Yes, we have 99 such articles in our textbook and access to all tasks and all hidden texts in them can be opened immediately.
Access to all hidden tasks is provided for the ENTIRE life of the site.
In conclusion...
If you don't like our tasks, find others. Just don't stop at theory.
“Understood” and “I can solve” are completely different skills. You need both.
Find problems and solve them!
Trigonometry, as a science, originated in the Ancient East. First trigonometric ratios were developed by astronomers to create an accurate calendar and navigate by the stars. These calculations related to spherical trigonometry, while in school course study the ratios of sides and angles of a plane triangle.
Trigonometry is a branch of mathematics that deals with the properties of trigonometric functions and the relationships between the sides and angles of triangles.
During the heyday of culture and science in the 1st millennium AD, knowledge spread from Ancient East to Greece. But the main discoveries of trigonometry are the merit of the men of the Arab Caliphate. In particular, the Turkmen scientist al-Marazwi introduced functions such as tangent and cotangent, and compiled the first tables of values for sines, tangents and cotangents. The concepts of sine and cosine were introduced by Indian scientists. Trigonometry received a lot of attention in the works of such great figures of antiquity as Euclid, Archimedes and Eratosthenes.
Basic quantities of trigonometry
Basic trigonometric functions numeric argument– these are sine, cosine, tangent and cotangent. Each of them has its own graph: sine, cosine, tangent and cotangent.
The formulas for calculating the values of these quantities are based on the Pythagorean theorem. It is better known to schoolchildren in the formulation: “Pythagorean pants are equal in all directions,” since the proof is given using the example of an isosceles right triangle.
Sine, cosine and other dependencies establish the relationship between sharp corners and sides of any right triangle. Let us give formulas for calculating these quantities for angle A and trace the relationships between trigonometric functions:

As can be seen, tg and ctg are inverse functions. If we imagine leg a as the product of sin A and hypotenuse c, and leg b as cos A * c, we obtain the following formulas for tangent and cotangent:

Trigonometric circle
Graphically, the relationship between the mentioned quantities can be represented as follows:

Circumference, in in this case, represents all possible values of the angle α - from 0° to 360°. As can be seen from the figure, each function takes a negative or positive value depending on the angle. For example, sin α will have a “+” sign if α belongs to the 1st and 2nd quarters of the circle, that is, it is in the range from 0° to 180°. For α from 180° to 360° (III and IV quarters), sin α can only be a negative value.
Let's try to build trigonometric tables for specific angles and find out the value of the quantities.

Values of α equal to 30°, 45°, 60°, 90°, 180° and so on are called special cases. The values of trigonometric functions for them are calculated and presented in the form of special tables.

These angles were not chosen at random. The designation π in the tables is for radians. Rad is the angle at which the length of a circle's arc corresponds to its radius. This value was introduced in order to establish a universal dependence; when calculating in radians, the actual length of the radius in cm does not matter.

Angles in tables for trigonometric functions correspond to radian values:

So, it is not difficult to guess that 2π is a complete circle or 360°.
Properties of trigonometric functions: sine and cosine
In order to consider and compare the basic properties of sine and cosine, tangent and cotangent, it is necessary to draw their functions. This can be done in the form of a curve located in a two-dimensional coordinate system.
Consider comparison table properties for sine and cosine:

| Sine wave | Cosine |
|---|---|
| y = sin x | y = cos x |
| ODZ [-1; 1] | ODZ [-1; 1] |
| sin x = 0, for x = πk, where k ϵ Z | cos x = 0, for x = π/2 + πk, where k ϵ Z |
| sin x = 1, for x = π/2 + 2πk, where k ϵ Z | cos x = 1, at x = 2πk, where k ϵ Z |
| sin x = - 1, at x = 3π/2 + 2πk, where k ϵ Z | cos x = - 1, for x = π + 2πk, where k ϵ Z |
| sin (-x) = - sin x, i.e. the function is odd | cos (-x) = cos x, i.e. the function is even |
| the function is periodic, the smallest period is 2π | |
| sin x › 0, with x belonging to the I and II quarters or from 0° to 180° (2πk, π + 2πk) | cos x › 0, with x belonging to the I and IV quarters or from 270° to 90° (- π/2 + 2πk, π/2 + 2πk) |
| sin x ‹ 0, with x belonging to the third and fourth quarters or from 180° to 360° (π + 2πk, 2π + 2πk) | cos x ‹ 0, with x belonging to the 2nd and 3rd quarters or from 90° to 270° (π/2 + 2πk, 3π/2 + 2πk) |
| increases in the interval [- π/2 + 2πk, π/2 + 2πk] | increases on the interval [-π + 2πk, 2πk] |
| decreases on intervals [π/2 + 2πk, 3π/2 + 2πk] | decreases on intervals |
| derivative (sin x)’ = cos x | derivative (cos x)’ = - sin x |
Determining whether a function is even or not is very simple. It is enough to imagine a trigonometric circle with the signs of trigonometric quantities and mentally “fold” the graph relative to the OX axis. If the signs coincide, the function is even, otherwise it is odd.

The introduction of radians and the listing of the basic properties of sine and cosine waves allow us to present the following pattern:

It is very easy to verify that the formula is correct. For example, for x = π/2, the sine is 1, as is the cosine of x = 0. The check can be done by consulting tables or by tracing function curves for given values.
Properties of tangentsoids and cotangentsoids
The graphs of the tangent and cotangent functions differ significantly from the sine and cosine functions. The values tg and ctg are reciprocals of each other.


- Y = tan x.
- The tangent tends to the values of y at x = π/2 + πk, but never reaches them.
- The smallest positive period of the tangentoid is π.
- Tg (- x) = - tg x, i.e. the function is odd.
- Tg x = 0, for x = πk.
- The function is increasing.
- Tg x › 0, for x ϵ (πk, π/2 + πk).
- Tg x ‹ 0, for x ϵ (— π/2 + πk, πk).
- Derivative (tg x)’ = 1/cos 2 x.
Let's consider graphic image cotangentoids below in the text.

Main properties of cotangentoids:
- Y = cot x.
- Unlike the sine and cosine functions, in the tangentoid Y can take on the values of the set of all real numbers.
- The cotangentoid tends to the values of y at x = πk, but never reaches them.
- The smallest positive period of a cotangentoid is π.
- Ctg (- x) = - ctg x, i.e. the function is odd.
- Ctg x = 0, for x = π/2 + πk.
- The function is decreasing.
- Ctg x › 0, for x ϵ (πk, π/2 + πk).
- Ctg x ‹ 0, for x ϵ (π/2 + πk, πk).
- Derivative (ctg x)’ = - 1/sin 2 x Correct