Problemi s parametrom (grafičko rješenje) Uvod. Plan za rješavanje problema s parametrom pomoću grafičke metode. Grafička metoda rješavanja jednačina s parametrima
Jednačine s parametrima s pravom se smatraju jednom od najčešćih složeni zadaci u toku školske matematike. Upravo takvi zadaci iz godine u godinu završavaju na listi zadataka tipa B i C na jednom državni ispit Jedinstveni državni ispit. Međutim, među velikim brojem jednačina s parametrima, postoje one koje se lako mogu riješiti grafički. Razmotrimo ovu metodu na primjeru rješavanja nekoliko problema.
Pronađite zbroj cjelobrojnih vrijednosti broja a za koji je jednadžba |x 2 – 2x – 3| = a ima četiri korijena.
Rješenje.
Da bismo odgovorili na pitanje problema, napravimo grafove funkcija na jednoj koordinatnoj ravni
y = |x 2 – 2x – 3| i y = a.
Grafikon prve funkcije y = |x 2 – 2x – 3| dobiće se iz grafika parabole y = x 2 – 2x – 3 simetričnim prikazom u odnosu na x-osu onaj dio grafika koji je ispod ose Ox. Dio grafikona koji se nalazi iznad x-ose ostat će nepromijenjen.
Uradimo to korak po korak. Graf funkcije y = x 2 – 2x – 3 je parabola čiji su ogranci usmjereni prema gore. Da bismo izgradili njegov graf, nalazimo koordinate vrha. Ovo se može uraditi pomoću formule x 0 = -b/2a. Dakle, x 0 = 2/2 = 1. Da bismo pronašli koordinatu vrha parabole duž ordinatne ose, zamenimo rezultujuću vrednost za x 0 u jednadžbu dotične funkcije. Dobijamo da je y 0 = 1 – 2 – 3 = -4. To znači da vrh parabole ima koordinate (1; -4).
Zatim morate pronaći točke presjeka grana parabole s koordinatnim osa. U tačkama preseka grana parabole sa apscisnom osom, vrednost funkcije je nula. Stoga rješavamo kvadratnu jednačinu x 2 – 2x – 3 = 0. Njeni korijeni će biti tražene tačke. Prema Vietinoj teoremi imamo x 1 = -1, x 2 = 3.
U tačkama preseka grana parabole sa ordinatnom osom, vrednost argumenta je nula. Dakle, tačka y = -3 je tačka preseka grana parabole sa y-osom. Dobijeni grafikon je prikazan na slici 1.
Da bismo dobili grafik funkcije y = |x 2 – 2x – 3|, prikažimo dio grafika koji se nalazi ispod apscise simetrično u odnosu na x-osu. Dobijeni grafikon je prikazan na slici 2.
Grafikon funkcije y = a je prava paralelna sa apscisnom osom. To je prikazano na slici 3. Koristeći sliku, nalazimo da grafovi imaju četiri zajedničke tačke (i jednačina ima četiri korijena) ako a pripada intervalu (0; 4).
Cjelobrojne vrijednosti broja a iz rezultirajućeg intervala: 1; 2; 3. Da odgovorimo na pitanje zadatka, pronađimo zbir ovih brojeva: 1 + 2 + 3 = 6.
Odgovor: 6.
Pronađite aritmetičku sredinu cjelobrojnih vrijednosti broja a za koje je jednadžba |x 2 – 4|x| – 1| = a ima šest korijena.
Počnimo crtanjem funkcije y = |x 2 – 4|x| – 1|. Da bismo to učinili, koristimo jednakost a 2 = |a| 2 i odaberite cijeli kvadrat u submodularnom izrazu napisanom na desnoj strani funkcije:
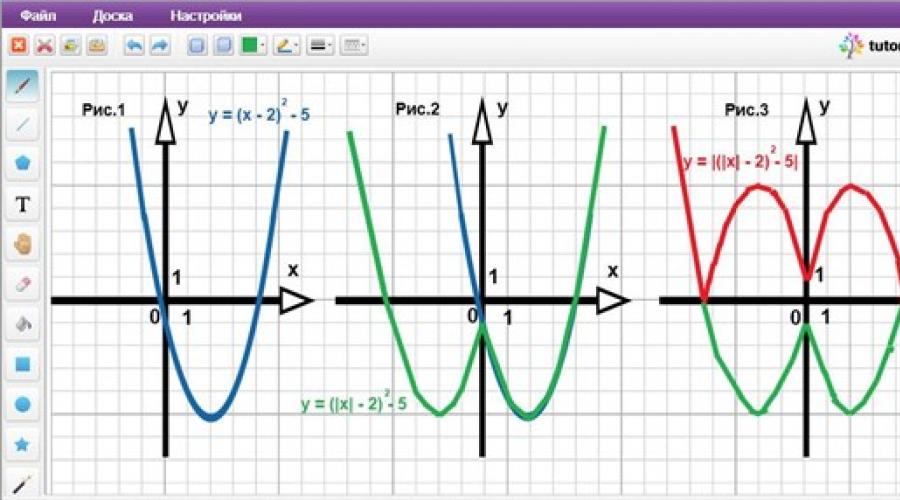
x 2 – 4|x| – 1 = |x| 2 – 4|x| - 1 = (|x| 2 – 4|x| + 4) – 1 – 4 = (|x |– 2) 2 – 5.
Tada će originalna funkcija imati oblik y = |(|x| – 2) 2 – 5|.
Da bismo konstruirali graf ove funkcije, konstruiramo sekvencijalne grafove funkcija:
1) y = (x – 2) 2 – 5 – parabola sa vrhom u tački sa koordinatama (2; -5); (Sl. 1).
2) y = (|x| – 2) 2 – 5 – dio parabole konstruisan u koraku 1, koji se nalazi desno od ordinatne ose, simetrično je prikazan lijevo od ose Oy; (Sl. 2).
3) y = |(|x| – 2) 2 – 5| – dio grafika konstruisan u tački 2, koji se nalazi ispod x-ose, prikazuje se simetrično u odnosu na x-osu prema gore. (Sl. 3).
Pogledajmo rezultirajuće crteže:
 Grafikon funkcije y = a je prava paralelna sa apscisnom osom.
Grafikon funkcije y = a je prava paralelna sa apscisnom osom.
Koristeći sliku, zaključujemo da grafovi funkcija imaju šest zajedničkih tačaka (jednačina ima šest korijena) ako a pripada intervalu (1; 5).
To se može vidjeti na sljedećoj slici:

Nađimo aritmetičku sredinu cjelobrojnih vrijednosti parametra a:
(2 + 3 + 4)/3 = 3.
Odgovor: 3.
blog.site, pri kopiranju materijala u cijelosti ili djelimično, potrebna je veza do originalnog izvora.
Kako bismo u potpunosti otkrili mogućnosti ove metode, razmotrit ćemo glavne vrste problema.
Primjeri zadataka za provjeru znanja i vještina pri rješavanju zadataka s parametrima grafičkom metodom (koordinatna ravan)
Zadatak 1.
Na kojim vrednostimaada li jednadžba = ima dva korijena?
Rješenje.
Pređimo na ekvivalentan sistem:
Ovaj sistem na koordinatnoj ravni (;) definira krivu. Jasno je da sve tačke ovog paraboličnog luka (i samo one) imaju koordinate koje zadovoljavaju prvobitnu jednačinu. Dakle, broj rješenja jednadžbe za svaku fiksnu vrijednost parametra, jednak broju presečnih tačaka krive sa horizontalnom linijom koja odgovara vrednosti ovog parametra.
Očigledno, kada označene linije sijeku graf u dvije tačke, što je ekvivalentno originalnoj jednačini koja ima dva korijena.
odgovor: at.
Zadatak 2.
Pronađite sve vrijednosti a za koje je sistem ima jedinstveno rešenje.
Rješenje.
Prepišimo originalni sistem u ovom obliku:
Sva rješenja ovog sistema (parovi forme) šrafiranjem formiraju područje prikazano na slici. Zahtjev za jedinstvenim rješenjem za dati sistem se prevodi na grafički jezik na sljedeći način: horizontalne linije moraju imati samo jednu zajedničku tačku sa rezultujućim regionom. To je lako vidjeti samo pravoi zadovoljavaju navedeni uslov.

odgovor: ili.
Dva zadatka o kojima smo upravo razgovarali omogućavaju nam da damo konkretnije preporuke u odnosu na one ranije:
pokušajte izraziti parametar kroz promjenljivu, tj. onda dobiti jednakosti oblika
nacrtati graf funkcije na ravni.
Zadatak 3.
Na kojim vrednostimaA da li jednadžba ima tačno tri korijena?
Rješenje.
Imamo
Graf ovog skupa je unija "ugla" i parabole. Očigledno, samo prava linija siječe rezultirajuću uniju u tri tačke.

odgovor: .
komentar: Parametar se obično uzima u obzir kao fiksni, ali nepoznati broj. U međuvremenu, sa formalne tačke gledišta, parametar je varijabla i „jednak“ ostalima prisutnim u problemu. Sa ovim prikazom parametra forme, funkcije se ne definiraju s jednom, već s dvije varijable.
Zadatak 4.
Pronađite sve vrijednosti parametara, za koje jednačina ima jedno rješenje.
Rješenje.
Razlomak je jednak nuli ako i samo ako je brojnik razlomka nula, a nazivnik nije nula.
Pronalaženje korijena kvadratni trinom:

Koristeći rezultujući sistem, lako je konstruisati graf originalne jednačine. Prisustvo „uboda“ u ovom grafikonu omogućava da jednačina ima jedinstveno rješenje kada i =. Ovo je odlučujući faktor u odluci.
Odgovori: I.
Zadatak 5.
Pri kojim vrijednostima parametara,A jednačina ima jedinstveno rješenje.
Rješenje.
Napišimo sistem koji je ekvivalentan originalnoj jednačini
Odavde dobijamo
Napravimo graf i nacrtajmo prave linije okomite na osiA .
Prve dvije nejednakosti sistema definiraju skup tačaka, prikazanih senčenjem, a ovaj skup ne uključuje hiperbole i.

Zatim segment i zraka, segment i zraka koji leže redom na linijama i , su graf originalne jednadžbe. Jedno rješenje će biti ako 2< < или < или = .
Odgovori : 2 < < или < или = .
Zadatak 6.
Pronađite sve vrijednosti parametaraA , za koje je jednadžba
ima tačno dva različita rješenja
Rješenje.
Razmotrimo skup od dva sistema
Ako , To.
Ako < , To.
Odavde
ili
Parabole i prava linija imaju dvije zajedničke tačke:A (-2; - 2), IN(-1; -1), i, IN – vrh prve parabole,D - vrh drugog. Dakle, graf izvorne jednačine je prikazan na slici.

Moraju postojati tačno dva različita rješenja. Ovo se radi sa ili.
odgovor: ili.
Zadatak 7.
Pronađite skup svih brojeva za svaki od kojih je jednačina
ima samo dva različita korijena.
Rješenje.
Prepišimo ovu jednačinu u obliku
Koreni jednačine, pod uslovom da.
Napravimo graf ove jednačine. IN u ovom slučaju Pogodno je konstruisati graf dodeljivanjem varijable ordinatnoj osi. Ovdje “čitamo” odgovor vertikalnim pravim linijama, nalazimo da ova jednadžba ima samo dva različita korijena na = -1 ili ili.

Isprekidane linije ukazuju na to.
odgovor: na = -1 ili ili.
Zadatak 8.
Za koje skup rješenja nejednakosti sadrži interval.
Rješenje.
Zapišimo skup od dva sistema ekvivalentna originalnoj jednadžbi:
ili
Pošto rješenje za prvi sistem nemaA segment ne može biti uključen, onda ćemo izvršiti potrebne studije za drugi sistem.
Imamo
Označimo . Tada druga nejednakost sistema poprima oblik< - a na koordinatnoj ravni definira skup prikazan na slici.

Pomoću slike utvrđujemo da kada rezultirajući skup sadrži sve tačke čije apscise prolaze kroz sve vrijednosti intervala
Onda, odavde.
Odgovori : .
Zadatak 9.
Pronađite sve nenegativne brojeve za koje postoji jedinstveni broj koji zadovoljava sistem
Rješenje.
Imamo
Prva jednadžba na koordinatnoj ravni specificira familiju vertikalnih linija. Prave linije i podijelite ravnine na četiri područja. Neki od njih su rješenja za sistem nejednakosti. Koje se tačno mogu odrediti uzimanjem testne tačke iz svake regije. Područje čija tačka zadovoljava nejednakost je njeno rješenje (ova tehnika je povezana s metodom intervala pri rješavanju nejednakosti sa jednom promjenljivom). Izgradnja pravih linija
Na primjer, uzimamo tačku i zamjenjujemo je u koordinate tačaka koje zadovoljavaju nejednakost.

Dobijamo dvije oblasti (I) I ( II), ali s obzirom da pod uslovom uzimamo samo površinu (I). Izgradnja pravih linija , k .
Dakle, originalni sistem zadovoljavaju sve tačke (i samo one) koje leže na zracima i istaknute na crtežu podebljanim linijama (tj. konstruišemo tačke u datoj oblasti).
Sada moramo pronaći jedinstvenu za fiksnu. Gradimo paralelne linije koje sijeku osu. i pronađite gdje će biti jedna tačka preseka sa pravom.
Iz slike nalazimo da je zahtjev jedinstvenosti rješenja postignut ako (za već 2 boda),
gdje je ordinata tačke preseka pravih i,
gdje je ordinata točke presjeka pravih i.
Tako da dobijamo< .
odgovor: < .
Zadatak 10.
Pri kojim vrijednostima parametra sistem ima rješenja?
Rješenje.
Hajde da faktorizujemo lijevoj strani sistemske nejednakosti, imamo
Gradimo prave linije i... Na slici prikazujemo senčenjem skup tačaka ravni koji zadovoljava nejednakost sistema.

Gradimo hiperbolu = .
Tada su apscise odabranih lukova hiperbole rješenja originalnog sistema.M , P , N , Q – čvorne tačke. Nađimo njihove apscise.
Za bodove P , Q imamo
Ostaje zapisati odgovor: ili.
odgovor: ili.
Zadatak 11.
Pronađite sve vrijednosti za koje nijedno rješenje nejednakosti u modulu ne prelazi dva ().
Rješenje .
Prepišimo ovu nejednakost u ovom obliku. Napravimo grafove jednadžbi i =.
Koristeći “metodu intervala” utvrđujemo da će rješenje izvorne nejednakosti biti zasjenjena područja.

Sada izgradimo područje i pogledajte koji dio pada u zasjenjeno područje.
One. sada, ako za neku fiksnu vrijednost prava linija na sjecištu s rezultujućom površinom daje samo tačke čije apscise zadovoljavaju uvjet < 2, tada je jedna od željenih vrijednosti parametra.
Vidimo to.
odgovor: .
Zadatak 12.
Za koje vrijednosti parametra skup rješenja nejednakosti ne sadrži više od četiri cjelobrojne vrijednosti?
Rješenje.
Pretvorimo ovu nejednakost u formu. Ova nejednakost je ekvivalentna kombinaciji dva sistema
ili

Koristeći ovaj skup, prikazujemo rješenje izvorne nejednakosti.
Hajde da nacrtamo prave linije gde. Tada će vrijednost za koju prava siječe prave u ne više od četiri tačke od označenog skupa biti željena. Dakle, vidimo da je ili ili.
odgovor: ili ili.
Zadatak 13.
Na kojim vrijednostima parametaraA ima sistem rješenja
Rješenje.
Korijeni kvadratnog trinoma i.
Onda
Gradimo prave linije i...
Koristeći metodu “intervala” nalazimo rješenje za sistemsku nejednakost (osjenčano područje).

Taj dio kruga sa centrom u početnoj točki i radijusom 2 koji spada u osenčenu oblast biće rešenje za ovaj sistem. .
Pronalazimo vrijednosti iz sistema
Značenje i je iz sistema.
odgovor:
Zadatak 14.
Ovisno o vrijednostima parametaraA riješiti nejednakost > .
Rješenje.
Prepišimo ovu nejednakost u obliku i razmotrimo funkciju, koje, proširujući module, pišemo na sljedeći način:

Pravimo raspored. Graf dijeli koordinatnu ravan na dva regiona. Uzimajući t (0; 0) i zamjenom i u originalnu nejednakost, dobijamo da je 0 > 1, pa je stoga originalna nejednakost zadovoljena u području grafa koji leži iznad.
Direktno sa slike dobijamo:
nema rješenja;
at ;
at.
odgovor: nema rješenja;
at ;
at.
Zadatak 15.
Pronađite sve vrijednosti parametra za koje je sistem nejednakosti
zadovoljan je samo jednim.
Rješenje.
Prepišimo ovaj sistem u ovom obliku:
Hajde da konstruišemo region definisan ovim sistemom.
1) , je vrh parabole.
2) - prava linija koja prolazi kroz tačke i.

Zahtjev za jedinstvenost rješenja preveden je na grafički jezik na sljedeći način: horizontalne linije sa rezultirajućom površinom moraju imati samo jednu zajedničku tačku. Navedeni zahtjev zadovoljavaju prave linije i, gdje je ordinata tačke preseka parabole i prave.
Nađimo vrijednost:
= (nije pogodno za značenje zadatka),
Pronalaženje ordinate:
Odgovor: ,
Zadatak 16.
Pronađite sve vrijednosti parametaraA, pod kojim sistem nejednakosti
zadovoljava samo za jedan x.
Rješenje .
Konstruirajmo parabole i pokažimo senčenjem rješenje posljednjeg sistema.

1) , .
2) , .
Slika pokazuje da je uslov problema zadovoljen kada ili.
odgovor: ili.
Zadatak 17.
Za koje vrijednosti jednačina ima tačno tri korijena?
Rješenje.
Ova jednačina je ekvivalentna skupu
Grafikon stanovništva je kombinacija grafova parabole i uglova.

Prave sijeku rezultirajuću uniju u tri tačke.
odgovor: at.
Zadatak 18.
Za koje vrijednosti jednačina ima tačno tri rješenja?
Rješenje.
Transformirajmo lijevu stranu ove jednačine. Dobijamo kvadratnu jednačinu u odnosu na.
Dobijamo jednačinu
Što je ekvivalentno totalitetu

Unija grafova parabola je rješenje za populaciju.
Pronađite ordinatne tačke preseka parabola:
Čitamo potrebne informacije sa slike: ova jednačina ima tri rješenja na ili
odgovor: na ili
Zadatak 19.
Ovisno o parametru, odredite broj korijena jednadžbe
Rješenje .
Smatrajte ovu jednačinu kvadratnom u odnosu na a.
,
.
Dobijamo totalitet

Gradimo grafove jednadžbi stanovništva i odgovaramo na pitanje postavljeno u zadatku.
odgovor:: nema rješenja;
: jedno rješenje;
: dva rješenja;
ili: tri rješenja;
ili: četiri rješenja.
Zadatak 20.
Koliko rješenja ima sistem?
Rješenje.
Jasno je da je broj korijena druge jednačine sistema jednak broju rješenja samog sistema.
Imamo, .
Smatrajući ovu jednačinu kvadratnom jednačinom, dobijamo skup.
Sada pristup koordinatnoj ravni čini zadatak jednostavnim. Koordinate presječnih tačaka nalazimo rješavanjem jednačine

Odavde
Vrhovi parabola i.
Odgovor: četiri rješenja;
: dva rješenja;
: jedno rješenje;
: nema rješenja.
Zadatak 21.
Pronađite sve realne vrijednosti parametra za koji jednadžba ima samo dva različita korijena. Zapišite ove korijene.
Rješenje .
Nađimo korijene kvadratnog trinoma u zagradama:

Opišimo skup rješenja ove jednadžbe u koordinatnoj ravni konstruiranjem grafova pod uvjetom da
Čitamo potrebne informacije sa slike. Dakle, ova jednadžba ima dva različita korijena na (i) i na (i)
Odgovor: na (i) i
kod (i).
Zadatak 2 2 .
Riješite sistem nejednačina:
Rješenje.

Konstruišemo grafove parabola i pravih linija u ravni.
Sve tačke u zasjenjenom području su rješenje za sistem. Podijelimo izgrađeno područje na dva dijela.
Ako je tako, onda nema rješenja.
Ako, tada će apscisa tačaka zasjenjenog područja biti veća od apscise tačaka prave linije, ali manja od apscise (većeg korijena jednadžbe) parabole.
Izrazimo to kroz jednačinu pravolinijske:
Nađimo korijene jednačine:
Onda.
Ako je tako, onda.
odgovor: za i 1 nema rješenja;
at;
at.
Zadatak 23.
Riješite sistem nejednačina
Rješenje.
– vrh parabole.
Vrh parabole.
Pronađite apscisu presječnih tačaka parabola:

Zasjenjeno područje je rješenje sistema. Hajde da ga podelimo na dva dela.
U jednadžbama parabola izražavamo ih kroz:
Hajde da to zapišemo odgovor:
ako i, onda nema rješenja;
ako, onda< ;
ako, onda.
Zadatak 24.
Na kojim vrijednostima i jednačina nema rješenja?
Rješenje.
Jednačina je ekvivalentna sistemu
Konstruirajmo mnoga rješenja sistema.

Tri dijela parabole su rješenje ove jednačine.
Pronađimo na kojem i isključimo ga.
Dakle, jer nema rješenja;
kada nema rješenja;
(napomena: za ostaloApostoji jedno ili dva rješenja).
odgovor: ; .
Zadatak 25.
Za koje stvarne vrijednosti parametra postoji barem jedan koji zadovoljava uvjete:
Rješenje.
Rešimo nejednakost grafički koristeći “intervalnu metodu” i napravimo graf. Pogledajmo koji dio grafa spada u konstruirano područje za rješavanje nejednakosti i nađemo odgovarajuće vrijednostiA.
Gradimo grafove pravih linija i
Oni dijele koordinatnu ravan na 4 regije.
Posljednju nejednačinu riješit ćemo grafički metodom intervala.
Zasjenjeno područje je njegovo rješenje. Dio grafa parabole spada u ovo područje. Na intervalu; (po uslovu, nejednakost sistema je stroga) postoje koji zadovoljavaju uslove datog sistema.

odgovor:
Zadatak 26.
Pronađite sve vrijednosti parametra za svaku od kojih skup rješenja nejednakosti ne sadrži niti jedno rješenje nejednakosti.
Rješenje.

Konstruirajmo skup rješenja nejednakosti („koristeći metodu intervala“). Zatim ćemo konstruisati “traku” traženih vrijednosti parametaraq one u kojima nijedna točka navedenih područja ne pripada „traci“
odgovor: ili.
Zadatak 27.
Za koje vrijednosti parametra jednadžba ima jedinstveno rješenje?
Rješenje.
Razložimo brojilac razlomka.
Ova jednačina je ekvivalentna sistemu:
Napravimo graf stanovništva u koordinatnoj ravni.
ili
– tačka preseka linija i. Grafikon populacije je unija pravih linija.
„Izbušite“ tačke na grafikonu sa apscisama.

Crtamo prave linije i vidimo gdje se nalazi jedna tačka presjeka sa grafikom.
Očigledno je da samo za ili da ova jednačina ima jedinstveno rješenje.
odgovor: ili.
Zadatak 28.
Za koje realne vrijednosti parametra sistem nejednačina nema rješenja?
Rješenje.

Skup ravnih tačaka zasjenjenog područja zadovoljava ovaj sistem nejednakosti.
Gradimo ravne linije. Sa slike utvrđujemo da kada je ( je apscisa točke presjeka hiperbole i prave), prave ne sijeku zasjenjeno područje.
odgovor: at.
Zadatak 29.
Na kojim vrijednostima parametaraA sistem ima jedinstveno rešenje.
Rješenje.
Pređimo na sistem koji je ekvivalentan ovom.
U koordinatnoj ravni ćemo konstruisati grafove parabola i vrhova parabola, respektivno, tačaka i.
Izračunajmo apscise presječnih tačaka parabola rješavanjem jednačine
Osjenčano područje je rješenje za sistem nejednakosti. Direktno i

ima jednu zajedničku tačku sa zasjenjenim područjem.
odgovor: na i.
Zadatak 30.
Riješite nejednačinu:
Rješenje.
Ovisno o parametru, naći ćemo vrijednost.
Nejednakost ćemo riješiti korištenjem “intervalne metode”.
Napravimo parabole
: .
Izračunajmo koordinate presečne tačke parabola:

Tačke u zasjenjenom području zadovoljavaju ovu nejednakost. Crtajući pravu liniju, ovu oblast dijelimo na tri dijela.
1) Ako, onda nema rješenja.
2) Ako, onda u jednačini to izražavamo kroz:
Dakle, na područjuI imamo.
Ako jeste, onda pogledajte:
a) region II .
Izrazimo to u jednačini kroz.
Manji korijen
Veći korijen.
Dakle, u okolini II imamo.
b) region III : .
odgovor: kada nema rješenja;
at
u, .
književnost:
Galitsky M. L., Goldman A. M., Zvavich L. I. Zbirka zadataka iz algebre za 8. – 9. razred: Tutorial za učenike škola i odeljenja sa višim studijama matematike - 2. izd. – M.: Obrazovanje, 1994.
P. I. Gornshtein, V. B. Polonsky, M. S. Yakir. Problemi sa parametrima. 3. izdanje, prošireno i revidirano. – M.: Ilexa, Harkov: Gimnazija, 2003.
Faddeev D.K. Algebra 6 – 8. – M.: Obrazovanje, 1983 (b – ka nastavnik matematike).
A.H. Shakhmeister. Jednačine i nejednačine s parametrima. Uredio B. G. Ziv. S – Petersburg. Moskva. 2004.
V. V. Amelkin, V. L. Rabtsevich. Problemi sa parametrima Minsk “Asar”, 2002.
A.H. Shakhmeister. Problemi s parametrima na Jedinstvenom državnom ispitu. Izdavačka kuća Moskovskog univerziteta, CheRo na Nevi MTsNMO.
TO zadaci sa parametrom može uključiti, na primjer, traženje rješenja za linearne i kvadratne jednadžbe u opšti pogled, proučavanje jednadžbe za broj dostupnih korijena ovisno o vrijednosti parametra.
Bez davanja detaljnih definicija, razmotrite sljedeće jednadžbe kao primjere:
y = kx, gdje su x, y varijable, k je parametar;
y = kx + b, gdje su x, y varijable, k i b parametri;
ax 2 + bx + c = 0, gdje su x varijable, a, b i c su parametar.
Rješavanje jednadžbe (nejednakosti, sistema) sa parametrom znači, po pravilu, rješavanje beskonačan skup jednačine (nejednačine, sistemi).
Zadaci sa parametrom mogu se podijeliti u dvije vrste:
A) uslov kaže: riješi jednadžbu (nejednakost, sistem) - to znači, za sve vrijednosti parametra pronaći sva rješenja. Ako barem jedan slučaj ostane neistražen, takvo rješenje se ne može smatrati zadovoljavajućim.
b) potrebno je navesti moguće vrijednosti parametra kod kojih jednačina (nejednakost, sistem) ima određena svojstva. Na primjer, ima jedno rješenje, nema rješenja, ima rješenja koja pripadaju intervalu, itd. U takvim zadacima potrebno je jasno naznačiti pri kojoj vrijednosti parametra je traženi uslov zadovoljen.
Parametar, budući da je nepoznat fiksni broj, ima neku vrstu posebne dvojnosti. Prije svega, potrebno je uzeti u obzir da pretpostavljena popularnost ukazuje da se parametar mora percipirati kao broj. Drugo, sloboda manipulisanja parametrom ograničena je njegovom nejasnošću. Na primjer, operacije dijeljenja izrazom koji sadrži parametar ili izvlačenje korijena parnog stepena iz takvog izraza zahtijevaju preliminarno istraživanje. Stoga je potrebna pažnja pri rukovanju parametrom.
Na primjer, da biste uporedili dva broja -6a i 3a, morate uzeti u obzir tri slučaja:
1) -6a će biti veće od 3a ako je a negativan broj;
2) -6a = 3a u slučaju kada je a = 0;
3) -6a će biti manje od 3a ako je a pozitivan broj 0.
Rješenje će biti odgovor.
Neka je data jednadžba kx = b. Ova jednadžba je kratka forma za beskonačan broj jednačina s jednom promjenljivom.
Prilikom rješavanja takvih jednadžbi mogu postojati slučajevi:
1. Neka je k bilo koji realan broj koji nije jednak nuli i b bilo koji broj iz R, tada je x = b/k.
2. Neka je k = 0 i b ≠ 0, originalna jednačina će imati oblik 0 x = b. Očigledno, ova jednačina nema rješenja.
3. Neka su k i b brojevi jednaki nuli, tada imamo jednakost 0 x = 0. Njeno rješenje je bilo koji realan broj.
Algoritam za rješavanje ove vrste jednadžbe:
1. Odredite “kontrolne” vrijednosti parametra.
2. Riješite originalnu jednačinu za x za vrijednosti parametara koje su određene u prvom paragrafu.
3. Riješite originalnu jednadžbu za x za vrijednosti parametara različite od onih odabranih u prvom paragrafu.
4. Odgovor možete napisati u sljedećem obliku:
1) za ... (vrijednosti parametara), jednačina ima korijen ...;
2) za ... (vrijednosti parametara), nema korijena u jednadžbi.
Primjer 1.
Riješite jednadžbu s parametrom |6 – x| = a.
Rješenje.
Lako je vidjeti da je ovdje a ≥ 0.
Prema pravilu modula 6 – x = ±a, izražavamo x:
Odgovor: x = 6 ± a, gdje je a ≥ 0.
Primjer 2.
Riješite jednačinu a(x – 1) + 2(x – 1) = 0 u odnosu na varijablu x.
Rješenje.
Otvorimo zagrade: ah – a + 2h – 2 = 0
Zapišimo jednačinu standardni obrazac: x(a + 2) = a + 2.
Ako izraz a + 2 nije nula, tj. ako je a ≠ -2, imamo rješenje x = (a + 2) / (a + 2), tj. x = 1.
Ako je a + 2 jednako nuli, tj. a = -2, tada imamo tačnu jednakost 0 x = 0, pa je x bilo koji realan broj.
Odgovor: x = 1 za a ≠ -2 i x € R za a = -2.
Primjer 3.
Riješite jednačinu x/a + 1 = a + x u odnosu na varijablu x.
Rješenje.
Ako je a = 0, onda pretvaramo jednačinu u oblik a + x = a 2 + ax ili (a – 1)x = -a(a – 1). Posljednja jednadžba za a = 1 ima oblik 0 x = 0, stoga je x bilo koji broj.
Ako je a ≠ 1, tada će posljednja jednačina imati oblik x = -a.
Ovo rješenje se može ilustrirati na koordinatnoj liniji (sl. 1)
Odgovor: nema rješenja za a = 0; x – bilo koji broj sa a = 1; x = -a za a ≠ 0 i a ≠ 1.
Grafička metoda
Razmotrimo još jedan način rješavanja jednadžbi s parametrom - grafički. Ova metoda se koristi prilično često.
Primjer 4.
U zavisnosti od parametra a, koliko korijena ima jednačina ||x| – 2| = a?
Rješenje.
Za rješavanje pomoću grafičke metode, konstruiramo grafove funkcija y = ||x| – 2| i y = a (sl. 2).
Na crtežu su jasno prikazani mogući slučajevi položaja prave linije y = a i broj korijena u svakoj od njih.
Odgovor: jednadžba neće imati korijen ako je a< 0; два корня будет в случае, если a >2 i a = 0; jednadžba će imati tri korijena u slučaju a = 2; četiri korena – na 0< a < 2.

Primjer 5.
Pri čemu je jednačina 2|x| + |x – 1| = a ima jedan korijen?
Rješenje.
Oslikajmo grafove funkcija y = 2|x| + |x – 1| i y = a. Za y = 2|x| + |x – 1|, proširivanjem modula metodom intervala, dobijamo:
(-3x + 1, na x< 0,
y = (x + 1, za 0 ≤ x ≤ 1,
(3x – 1, za x > 1.
On Slika 3 Jasno se vidi da će jednadžba imati jedan korijen samo kada je a = 1.
Odgovor: a = 1.
Primjer 6.
Odrediti broj rješenja jednadžbe |x + 1| + |x + 2| = a u zavisnosti od parametra a?
Rješenje.
Grafikon funkcije y = |x + 1| + |x + 2| će biti izlomljena linija. Njegovi vrhovi će se nalaziti u tačkama (-2; 1) i (-1; 1) (Slika 4).
Odgovor: ako je parametar a manji od jedan, tada jednačina neće imati korijene; ako je a = 1, tada je rješenje jednadžbe beskonačan skup brojeva iz intervala [-2; -1]; ako su vrijednosti parametra a veće od jedan, tada će jednadžba imati dva korijena.
Imate još pitanja? Ne znate kako riješiti jednadžbe s parametrom?
Da biste dobili pomoć od tutora, registrujte se.
Prva lekcija je besplatna!
web stranicu, kada kopirate materijal u cijelosti ili djelomično, link na izvor je obavezan.
Za svaku vrijednost parametra a a riješite nejednakost | 2 x + a | ≤ x + 2 |2x+a| \leq x+2 .
Prvo, riješimo pomoćni problem. Razmotrimo ovu nejednakost kao nejednakost sa dvije varijable x x i a a i nacrtajmo na koordinatnoj ravni x O a xOa sve tačke čije koordinate zadovoljavaju nejednakost.
Ako je 2 x + a ≥ 0 2x+a \geq 0 (tj. na pravoj liniji a = - 2 x a=-2x i više), onda dobijamo 2 x + a ≤ x + 2 ⇔ a ≤ 2 - x 2x+ a \leq x+2 \leftrightarrow a \leq 2-x .
Set je prikazan na sl. 11.
Sada da riješimo originalni problem koristeći ovaj crtež. Ako popravimo a a , onda ćemo dobiti horizontalnu ravnu liniju a = const a = \textrm(const) . Da biste odredili vrijednosti x x, morate pronaći apscisu točaka presjeka ove linije sa skupom rješenja nejednakosti. Na primjer, ako je a = 8 a=8, tada nejednakost nema rješenja (prava linija ne siječe skup); ako je a = 1 a=1 , tada su rješenja sva x x iz segmenta [ - 1 ; 1 ] [-1;1] itd. Dakle, moguće su tri opcije.
1) Ako je $$a>4$$, onda nema rješenja.
2) Ako je a = 4 a=4, onda je x = - 2 x=-2.
ODGOVOR
na $$a
za a = 4 a=4 - x = - 2 x=-2 ;
za $$a>4$$ - nema rješenja.
Pronađite sve vrijednosti parametra a a za koje vrijedi nejednakost $$3-|x-a| > x^2$$ a) ima najmanje jedno rješenje; b) ima najmanje jedno pozitivno rješenje.
Prepišimo nejednačinu u obliku $$3-x^2 > |x-a)$$. Napravimo grafove lijevog i desnog dijela na ravni x O y xOy. Graf lijeve strane je parabola sa granama prema dolje sa vrhom u tački (0; 3) (0;3) . Graf siječe x-osu u tačkama (± 3 ; 0) (\pm \sqrt(3);0) . Grafikon desne strane je ugao sa vrhom na x-osi, čije su stranice usmjerene prema gore pod uglom od 45°45^(\circ) u odnosu na koordinatne ose. Apscisa temena je tačka x = a x=a .
a) Da bi nejednačina imala barem jedno rješenje, potrebno je i dovoljno da se barem u jednoj tački parabola nalazi iznad grafika y = | x - a | y=|x-a| . Ovo se postiže ako vrh ugla leži između tačaka A A i B B ose apscise (vidi sliku 12 - tačke A A i B B nisu uključene). Dakle, potrebno je odrediti na kojoj poziciji vrha jedna od grana ugla dodiruje parabolu.

Razmotrimo slučaj kada je vrh ugla u tački A A. Tada desna grana ugla dodiruje parabolu. Njegov nagib je jednak jedan. To znači da je derivacija funkcije y = 3 - x 2 y = 3-x^2 u tački tangentnosti jednaka 1 1, tj. - 2 x = 1 -2x=1, odakle je x = - 1 2 x = -\frac( 1)(2) . Tada je ordinata tačke tangente y = 3 - (1 2) 2 = 11 4 y = 3 - (\frac(1)(2))^2 = \frac(11)(4) . Jednadžba prave linije koja ima ugaoni koeficijent k = 1 k=1 i koja prolazi kroz tačku sa koordinatama (- 1 2 ; 11 4) (-\frac(1)(2); \frac(11)(4) ) je sljedeće * ( \^* : y - 11 4 = 1 · (x + 1 2) y - \frac{11}{4} = 1 \cdot (x+ \frac{1}{2}) , откуда y = x + 13 4 y = x + \frac{13}{4} .!}
Ovo je jednadžba desne grane ugla. Apscisa tačke preseka sa x osom je jednaka - 13 4 -\frac(13)(4), tj. tačka A A ima koordinate A (- 13 4 ; 0) A(-\frac(13)(4 0) . Iz razloga simetrije, tačka B B ima koordinate: B (13 4 ; 0) B(\frac(13)(4); 0) .
Odavde dobijamo da je a ∈ (- 13 4 ; 13 4) a\in (-\frac(13)(4); \frac(13)(4)) .
b) Nejednačina ima pozitivna rješenja ako je vrh ugla između tačaka F F i B B (vidi sliku 13). Pronalaženje položaja tačke F F nije teško: ako je vrh ugla u tački F F, onda je njegova desna grana (prava linija data jednadžbom y = x - a y = x-a prolazi kroz tačku (0; 3 ) (0;3) Odavde nalazimo da je a = - 3 a=-3 i tačka F F ima koordinate (- 3 ; 0) (-3; 0) \in (-3; \frac(13)(4) ) .
ODGOVOR
a) a ∈ (- 13 4 ; 13 4) , a\in (-\frac(13)(4); \frac(13)(4)),\:\:\: b) a ∈ (- 3 13 4) a \in (-3; \frac(13)(4)) .
* {\^* Полезные формулы: !}
- \-- prava linija koja prolazi kroz tačku (x 0 ; y 0) (x_0;y_0) i ima ugaoni koeficijent k k data je jednadžbom y - y 0 = k (x - x 0) y-y_0= k(x-x_0 ) ;
- \-- ugaoni koeficijent prave linije koja prolazi kroz tačke (x 0 ; y 0) (x_0;y_0) i (x 1 ; y 1) (x_1;y_1), gdje je x 0 ≠ x 1 x_0 \neq x_1, izračunava se po formuli k = y 1 - y 0 x 1 - x 0 k = \dfrac(y_1-y_0)(x_1-x_0) .
Komentar. Ako trebate pronaći vrijednost parametra na kojoj se dodiruju prava linija y = k x + l y=kx+l i parabola y = a x 2 + b x + c y = ax^2+bx+c, tada možete napisati uslov da jednadžba k x + l = a x 2 + b x + c kx+l = ax^2+bx+c ima tačno jedno rješenje je u tački A A je sljedeća: jednačina x - a = 3 - x 2 x-a = 3-x^2 ima tačno jedno rješenje ⇔ D = 1 + 4 (a + 3) = 0 ⇔ a = - 13 4 \Leftrightarrow D = 1 + 4(a+3) = 0 \Leftrightarrow a = -\ dfrac(13)(4) .
Imajte na umu da je na ovaj način nemoguće zapisati uslov da linija dodiruje proizvoljan graf. Na primjer, prava y = 3 x - 2 y = 3x - 2 dodiruje kubičnu parabolu y = x 3 y=x^3 u tački (1 ; 1) (1;1) i siječe je u tački (- 2 ; - 8) (-2;-8), tj. jednačina x 3 = 3 x + 2 x^3 = 3x+2 ima dva rješenja.
Pronađite sve vrijednosti parametra a a , za svaku od kojih je jednadžba (a + 1 - | x + 2 |) (x 2 + 4 x + 1 - a) = 0 (a+1-|x+2| )(x^2 +4x+1-a) = 0 ima a) tačno dva različita korijena; b) tačno tri različita korijena.
Uradimo isto kao u primjeru 25. Opišimo skup rješenja ove jednačine na ravni x O a xOa . To je ekvivalentno kombinaciji dvije jednačine:
1) a = | x + 2 | - 1 a = |x+2| -1 je ugao sa granama prema gore i vrhom u tački (- 2 ; - 1) (-2;-1) .
2) a = x 2 + 4 x + 1 a = x^2 + 4x + 1 - ovo je parabola sa granama prema gore i vrhom u tački (- 2 ; - 3) (-2;-3) . Vidi sl. 14.

Nalazimo presečne tačke dva grafika. Desna grana ugla je data jednačinom y = x + 1 y=x+1 . Rješavanje jednačine
x + 1 = x 2 + 4 x + 1 x+1 = x^2+4x+1
nalazimo da je x = 0 x=0 ili x = - 3 x=-3 . Pogodna je samo vrijednost x = 0 x=0 (pošto je za desnu granu x + 2 ≥ 0 x+2 \geq 0). Tada je a = 1 a=1 . Slično, nalazimo koordinate druge točke presjeka - (- 4 ; 1) (-4; 1) .
Vratimo se prvobitnom problemu. Jednačina ima tačno dva rješenja za one a a za koje horizontalna linija a = const a=\textrm(const) siječe skup rješenja jednadžbe u dvije tačke. Iz grafa vidimo da ovo vrijedi za a ∈ (- 3 ; - 1) ∪ ( 1 ) a\in (-3;-1)\bigcup\(1\) . U slučaju će biti tačno tri rješenja tri boda raskrsnice, što je moguće samo kada je a = - 1 a=-1 .
ODGOVOR
a) a ∈ (- 3 ; - 1) ∪ ( 1 ) ;
a\in (-3;-1)\bigcup\(1\);\:\:\: b) a = - 1 a=-1 .
$$\begin(slučajevi) x^2-x-a \leq 0,\\ x^2+2x-6a \leq 0 \end(slučajevi) $$
ima tačno jedno rešenje.

Prva nejednakost je zadovoljena tačkama koje leže na paraboli a = - x 2 + x a = -x^2+x i ispod nje, a druga je zadovoljena tačkama koje leže na paraboli a = x 2 + 6 x 6 a = \dfrac(x^2 +6x)(6) i više. Pronalazimo koordinate vrhova parabola i njihovih presječnih tačaka, a zatim gradimo graf. Vrh prve parabole je (1 2 ; 1 4) (\dfrac(1)(2);\dfrac(1)(4)), vrh druge parabole je (- 1 ; - 1 6) ( -1 -\dfrac(1)(6)), tačke preseka su (0; 0) (0;0) i (4 7; 12 49) (\dfrac(4)(7); \dfrac(12; )(49)). Skup tačaka koje zadovoljavaju sistem prikazan je na Sl. 15. Može se vidjeti da horizontalna linija a = const a=\textrm(const) ima tačno jednu zajedničku tačku sa ovim skupom (što znači da sistem ima tačno jedno rješenje) u slučajevima a = 0 a=0 i a = 1 4 a= \dfrac(1)(4) .
ODGOVOR
A = 0 , a = 1 4 a=0,\: a=\dfrac(1)(4)
Nađi najmanju vrijednost parametar a a , za svaki od kojih je sistem
$$\begin(slučajevi) x^2+y^2 + 3a^2 = 2y + 2\sqrt(3)ax,\\ \sqrt(3)|x|-y=4 \end(slučajevi) $$
ima jedinstveno rešenje.
Transformirajmo prvu jednačinu, isticanje kompletnih kvadrata:
(x 2 - 2 3 a x + 3 a 2) + (y 2 - 2 y + 1) = 1 ⇔ (x - a 3) 2 + (y - 1) 2 = 1.
18 (x^2- 2\sqrt(3)ax+3a^2)+(y^2-2y+1)=1 \Leftrightarrow (x-a\sqrt(3))^2+(y-1)^2 =1. \:\:\:\lijevo(18\desno)
Za razliku od prethodnih problema, ovdje je bolje prikazati crtež na ravnini x O y xOy (crtež u ravnini "varijabla - parametar" obično se koristi za probleme s jednom varijablom i jednim parametrom - rezultat je skup na ravnini U ovom problemu imamo posla sa dve promenljive i parametrom. Crtanje skupa tačaka (x; y; a) u trodimenzionalnom prostoru je težak zadatak da bude vizuelno). Jednačina (18) određuje kružnicu sa centrom (a 3 ; 1) (a\sqrt(3);1) poluprečnika 1. Centar ove kružnice, u zavisnosti od vrijednosti a a, može se nalaziti u bilo kojoj tački na prava y = 1 y=1.

Druga jednadžba sistema je y = 3 | x | - 4 y = \sqrt(3)|x|-4 postavlja ugao sa stranicama nagore pod uglom od 60 ° 60^(\circ) na osu apscise (ugaoni koeficijent prave linije je tangenta ugao nagiba tg 60° = 3 \textrm(tg )(60^(\circ)) = \sqrt(3)), sa vrhom u tački (0; - 4) (0;-4) . Ovaj sistem jednadžbe imaju tačno jedno rješenje ako kružnica dodiruje jednu od grana ugla. Ovo je moguće učetiri slučaja (Sl. 16): centar kruga može biti u jednoj od tačaka A A, B B, C C, D D. Pošto treba da nađemo najmanju vrednost parametra a a, zanima nas apscisa tačke D D. Hajde da razmotrimo D H M D H M . Udaljenost od tačke D D do prave H M HM jednaka je poluprečniku kružnice, dakle D H = 1 DH=1. Dakle, D M = D H sin 60 ° = 2 3 DM=\dfrac(DH)(\textrm(sin)(60^(\circ))) = \dfrac(2)(\sqrt(3)) . Koordinate tačke M M nalaze se kao koordinate presečne tačke dve prave y = 1 y=1 i y = - 3 x - 4 y=-\sqrt(3)x-4 (leva strana ugla) .
Dobijamo M (- 5 3) M(-\dfrac(5)(\sqrt(3))) . Tada je apscisa tačke D D jednaka - 5 3 - 2 3 = - 7 3 -\dfrac(5)(\sqrt(3))-\dfrac(2)(\sqrt(3))=-\dfrac( 7)(\ sqrt(3)) .
Kako je apscisa centra kružnice jednaka a 3 a\sqrt(3) , slijedi da je a = - 7 3 a=-\dfrac(7)(3) .
ODGOVOR
A = - 7 3 a=-\dfrac(7)(3)
Pronađite sve vrijednosti parametra a a , za svaku od kojih je sistem
$$\begin(cases) |4x+3y| \leq 12a,\\ x^2+y^2 \leq 14ax +6ay -57a^2+16a+64 \end(slučajevi) $$
$$\begin(slučajevi) x^2-x-a \leq 0,\\ x^2+2x-6a \leq 0 \end(slučajevi) $$
Opišimo skupove rješenja svake od nejednačina na ravni x O y xOy.
U drugoj nejednakosti biramo savršene kvadrate:
x 2 - 14 a x + 49 + y 2 - 6 a y + 9 a 2 ≤ a 2 + 16 a + 64 ⇔ (x - 7 a) 2 + (y - 3 a) 2 ≤ (a + 8) 2 ) x^2-14ax+49 + y^2-6ay + 9a^2 \leq a^2 + 16a + 64 \Leftrightarrow (x-7a)^2+(y-3a)^2 \leq (a+8 )^2 \:\:\:\: (19)
Kada je a + 8 = 0 a+8=0 (a = - 8 a=-8), nejednakost (19) određuje tačku sa koordinatama (7 a ; 3 a) (7a;3a), tj. (- 56 ; - 24) (-56;-24) . Za sve ostale vrijednosti a (19) definira kružnicu sa centrom u tački (7a; 3a) (7a;3a) polumjera | a+8 | |a+8| .
Razmotrimo prvu nejednakost.
1) Za negativno a a nema rješenja. To znači da sistem nema rješenja.
2) Ako je a = 0 a=0, onda dobijamo pravu liniju 4 x + 3 y = 0 4x+3y=0. Iz druge nejednakosti dobijamo kružnicu sa centrom (0; 0) (0; 0) poluprečnika 8. Očigledno, postoji više od jednog rješenja.
3) Ako je $$a>0$$, onda je ova nejednakost ekvivalentna dvostrukoj nejednakosti - 12 a ≤ 4 x + 3 y ≤ 12 a -12a \leq 4x+3y \leq 12a . Definira traku između dvije prave linije y = ± 4 a - 4 x 3 y=\pm 4a -\dfrac(4x)(3) , od kojih je svaka paralelna pravoj liniji 4 x + 3 y = 0 4x+ 3y=0 (slika 17).

Pošto razmatramo $$a>0$$, centar kruga se nalazi u prvoj četvrtini na pravoj y = 3 x 7 y = \dfrac(3x)(7) . Zaista, koordinate centra su x = 7 a x=7a , y = 3 a y=3a ; izražavajući a a i izjednačavajući, dobijamo x 7 = y 3 \dfrac(x)(7)=\dfrac(y)(3) , odakle je y = 3 x 7 y = \dfrac(3x)(7) . Da bi sistem imao tačno jedno rešenje, potrebno je i dovoljno da kružnica dodiruje pravu liniju a 2 a_2 . Ovo se dešava kada je poluprečnik kružnice jednak udaljenosti od centra kružnice do prave a 2 a_2. Prema formuli za udaljenost od tačke do prave * (\^{*} получаем, что расстояние от точки (7 a ; 3 a) (7a;3a) до прямой 4 x + 3 y - 12 a = 0 4x+3y-12a=0 равно | 4 · 7 a + 3 · 3 a - 12 a | 4 2 + 3 2 = 5 a \dfrac{|4\cdot 7a + 3\cdot 3a -12a|}{\sqrt{4^2+3^2}} = 5\left|a\right| . Приравнивая к радиусу круга, получаем 5 a = | a + 8 | 5{a} = |a+8| . Так как $$a>0$$, опускаем модули и находим, что a = 2 a=2 .!}
ODGOVOR
A = 2 a=2
* {\^{*} Пусть даны точка M (x 0 ; y 0) M (x_0;y_0) и прямая l l , !} dato jednačinom a x + b y + c = 0 ax+by+c=0 . Tada je udaljenost od tačke M M do prave l l određena formulom ρ = | a x 0 + b x 0 + c | a 2 + b 2 \rho = \dfrac(|ax_0+bx_0+c|)(\sqrt(a^2+b^2)) .
Na kojim vrijednostima parametra a a radi sistem
$$\begin(cases) |x|+|y|=1,\\ |x+a|+|y+a|=1 \end(cases)$$ nema rješenja?
Prva jednadžba sistema definira kvadrat A B C D ABCD na ravni x O y xOy (da biste je konstruirali, razmotrite x ≥ 0 x\geq 0 i y ≥ 0 y\geq 0 . Tada jednačina poprima oblik x + y = 1 x+y=1 Dobijamo odsječak - dio prave linije x + y = 1 x+y=1, koji leži u prvoj četvrtini odražavaju rezultujući skup u odnosu na osu O y Oy (vidi sliku 18). Druga jednačina definiše kvadrat P Q R S PQRS , jednak kvadratu A B C D ABCD , ali sa centrom u tački (- a ; - a) (-a;-a) . Na sl. Kao primjer, slika 18 prikazuje ovaj kvadrat za a = - 2 a=-2. Sistem nema rješenja ako se ova dva kvadrata ne sijeku.

Lako je vidjeti da ako se segmenti P Q PQ i B C BC poklapaju, onda je centar drugog kvadrata u tački (1; 1) (1;1). Prikladne su nam one vrijednosti a kod kojih se centar nalazi "iznad" i "desno", tj. $$a1$$.
ODGOVOR
A ∈ (- ∞ ; - 1) ∪ (1 ; + ∞) a\in (-\infty;-1)\bigcup(1;+\infty) .
Pronađite sve vrijednosti parametra b b za koje je sistem
$$\begin(slučajevi) y=|b-x^2|,\\ y=a(x-b) \end(slučajevi) $$
ima barem jedno rješenje za bilo koju vrijednost a .
Razmotrimo nekoliko slučajeva.
1) Ako je $$b2) Ako je b = 0 b=0, tada sistem ima oblik $$\begin(cases) y=x^2,\\ y=ax .\end(cases) $$
Za bilo koje a a par brojeva (0 ; 0) (0;0) je rješenje ovog sistema, stoga je b = 0 b=0 pogodan.

3) Hajde da popravimo neke $$b>0$$. Prva jednačina je zadovoljena skupom tačaka dobijenih iz parabole y = x 2 - b y=x^2-b odbijanjem dijela ove parabole u odnosu na osu O x Ox (vidi sliku 19a, b). Druga jednačina definira familiju linija (zamjena različita značenja a a , možete dobiti sve vrste pravih linija koje prolaze kroz tačku (b ; 0) (b;0) , osim vertikalne, prolazeći kroz tačku (b ; 0) (b;0) . Ako tačka (b ; 0) (b;0) leži na segmentu [ - b ; b ] [-\sqrt(b);\sqrt(b)] . apscisa, tada prava linija siječe grafik prve funkcije za bilo koji nagib (slika 19a). U suprotnom (slika 19b) u svakom slučaju će postojati prava linija koja ne siječe ovaj graf. Rješavajući nejednačinu - b ≤ b ≤ b -\sqrt(b)\leq b \leq \sqrt(b) i uzimajući u obzir da je $$b>0$$, dobijamo da je b ∈ (0 ; 1 ] b \ u (0;1] .
Kombinujemo rezultate: $$b \u $$.
ODGOVOR
$$b \u $$
Pronađite sve vrijednosti a a, za svaku od kojih je funkcija f (x) = x 2 - | x - a 2 | - 3 x f(x) = x^2-|x-a^2|-3x ima najmanje jednu maksimalnu tačku.
Proširujući modul, dobijamo to
$$f(x) = \begin(slučajevi) x^2-4x+a^2, \:\:\: x\geq a^2 ,\\ x^2-2x-a^2, \:\ :\: x\leq a^2 . \end(slučajevi) $$
Na svakom od dva intervala, graf funkcije y = f (x) y=f(x) je parabola sa granama prema gore.

Pošto parabole sa granama nagore ne mogu imati maksimalne tačke, jedina mogućnost je da je tačka maksimuma granična tačka ovih intervala - tačka x = a 2 x=a^2 . U ovom trenutku će postojati maksimum ako vrh parabole y = x 2 - 4 x + a 2 y=x^2-4x+a^2 pada na interval $$x>a^2$$, i vrh parabole y = x 2 - 2 x - a 2 y=x^2-2x-a^2 - za interval $$x\lt a^2$$ (vidi sliku 20). Ovaj uslov je dat nejednačinama i $$2 \gt a^2$$ i $$1 \lt a^2$$, rješavanjem kojih nalazimo da je a ∈ (- 2 ; 1) ∪ (1 ; 2) a\in (-\ sqrt(2);1)\bigcup(1;\sqrt(2)) .
ODGOVOR
A ∈ (- 2 ; 1) ∪ (1 ; 2) a\in (-\sqrt(2);1)\bigcup(1;\sqrt(2))
Pronađite sve vrijednosti a a, za svaku od njih opšta rješenja nejednakosti
y + 2 x ≥ a y+2x \geq a i y - x ≥ 2 a (20) y-x \geq 2a \:\:\:\:\:\:\:\: (20)
su rješenja nejednakosti
$$2y-x>a+3 \:\:\:\:\:\:\:\:\: (21)$$
Za kretanje kroz situaciju, ponekad je korisno uzeti u obzir vrijednost jednog parametra. Napravimo crtež, na primjer, za a = 0 a=0 . Nejednačine (20) (zapravo, radi se o sistemu nejednačina (20)) zadovoljavaju tačke ugla B A C BAC (vidi sliku 21) - tačke, od kojih svaka leži iznad obe prave y = - 2 x y=-2x i y = x y =x (ili na ovim linijama). Nejednakost (21) je zadovoljena tačkama koje leže iznad prave linije y = 1 2 x + 3 2 y = \dfrac(1)(2)x + \dfrac(3)(2) . Može se vidjeti da kada je a = 0 a=0 uslov problema nije zadovoljen.

Šta će se promijeniti ako uzmemo drugu vrijednost za parametar a a ? Svaka od linija će se kretati i pretvoriti u pravu paralelnu sebi, budući da kutni koeficijenti pravih ne ovise o a a. Da bi uslov zadatka bio ispunjen, ceo ugao B A C BAC mora ležati iznad prave l l . Budući da su ugaoni koeficijenti pravih A B AB i A C AC veći u apsolutnoj vrijednosti nagib prava l l , potrebno je i dovoljno da vrh ugla leži iznad prave l l .
Rješavanje sistema jednačina
$$\begin(slučajevi) y+2x=a,\\ y-x=2a, \end(slučajevi)$$
pronaći koordinate tačke A (- a 3 ; 5 a 3) A(-\dfrac(a)(3);\dfrac(5a)(3)) . Moraju zadovoljiti nejednakost (21), pa $$\dfrac(10a)(3)+\dfrac(a)(3) > a+3$$, odakle $$a>\dfrac(9)(8)$$ .
ODGOVOR
$$a>\dfrac(9)(8)$$