Primjeri rješavanja logaritamskih nejednačina povećane složenosti. Sve o logaritamskim nejednačinama. Analiza primjera

Mislite li da ima još vremena do Jedinstvenog državnog ispita i da ćete imati vremena da se pripremite? Možda je to tako. Ali u svakom slučaju, što ranije student počne sa pripremama, to će uspješnije polagati ispite. Danas smo odlučili posvetiti članak logaritamskim nejednačinama. Ovo je jedan od zadataka, što znači mogućnost da dobijete dodatni kredit.

Da li već znate šta je logaritam? Zaista se nadamo. Ali čak i ako nemate odgovor na ovo pitanje, to nije problem. Razumjeti šta je logaritam je vrlo jednostavno.

Zašto 4? Morate podići broj 3 na ovaj stepen da dobijete 81. Kada shvatite princip, možete nastaviti sa složenijim proračunima.

Prošli ste kroz nejednakosti prije nekoliko godina. I od tada se stalno susrećete s njima u matematici. Ako imate problema s rješavanjem nejednakosti, pogledajte odgovarajući odjeljak.
Sada kada smo se upoznali sa konceptima pojedinačno, pređimo na njihovo razmatranje općenito.

Najjednostavnija logaritamska nejednakost.

Najjednostavnije logaritamske nejednakosti nisu ograničene na ovaj primjer, postoje još tri, samo s različitim predznacima. Zašto je ovo potrebno? Da bolje razumijemo kako riješiti nejednakosti logaritmima. Sada dajmo primjereniji primjer, još uvijek prilično jednostavan, ostavit ćemo složene logaritamske nejednakosti za kasnije.

Kako to riješiti? Sve počinje od ODZ-a. Vrijedi znati više o tome ako želite uvijek lako riješiti bilo koju nejednakost.

Šta je ODZ? ODZ za logaritamske nejednakosti

Skraćenica označava područje prihvatljive vrijednosti. Ova formulacija se često pojavljuje u zadacima za Jedinstveni državni ispit. ODZ će vam biti od koristi ne samo u slučaju logaritamskih nejednakosti.

Pogledajte ponovo gornji primjer. Na osnovu njega ćemo razmotriti ODZ, kako biste razumjeli princip, a rješavanje logaritamskih nejednačina ne postavlja pitanja. Iz definicije logaritma slijedi da 2x+4 mora biti veće od nule. U našem slučaju to znači sljedeće.

Ovaj broj, po definiciji, mora biti pozitivan. Riješite gore prikazanu nejednakost. Ovo se čak može učiniti i usmeno, ovdje je jasno da X ne može biti manji od 2. Rješenje nejednakosti će biti definicija raspona prihvatljivih vrijednosti.
Pređimo sada na rješavanje najjednostavnije logaritamske nejednakosti.

Odbacujemo same logaritme sa obe strane nejednakosti. Šta nam ovo ostavlja? Jednostavna nejednakost.

To nije teško riješiti. X mora biti veći od -0,5. Sada kombinujemo dve dobijene vrednosti u sistem. dakle,

Ovo će biti raspon prihvatljivih vrijednosti za logaritamsku nejednakost koja se razmatra.

Zašto nam je uopšte potreban ODZ? Ovo je prilika da se iskorijene netačni i nemogući odgovori. Ako odgovor nije u rasponu prihvatljivih vrijednosti, onda odgovor jednostavno nema smisla. Ovo je vrijedno pamćenja dugo vremena, jer u Jedinstvenom državnom ispitu često postoji potreba za traženjem ODZ-a, a ne tiče se samo logaritamskih nejednakosti.

Algoritam za rješavanje logaritamske nejednakosti

Rješenje se sastoji od nekoliko faza. Prvo morate pronaći raspon prihvatljivih vrijednosti. U ODZ-u će biti dva značenja, o tome smo raspravljali gore. Zatim moramo riješiti samu nejednakost. Metode rješenja su sljedeće:

• metoda zamjene množitelja;
• raspadanje;
• metoda racionalizacije.

Ovisno o situaciji, vrijedi koristiti jednu od gore navedenih metoda. Pređimo direktno na rješenje. Otkrijmo najpopularniju metodu, koja je pogodna za rješavanje zadataka Jedinstvenog državnog ispita u gotovo svim slučajevima. Zatim ćemo pogledati metodu dekompozicije. Može vam pomoći ako naiđete na posebno nezgodnu nejednakost. Dakle, algoritam za rješavanje logaritamske nejednakosti.

Primjeri rješenja :

Nije uzalud uzeli upravo ovu nejednakost! Obratite pažnju na bazu. Zapamtite: ako je veći od jedan, predznak ostaje isti prilikom pronalaženja raspona prihvatljivih vrijednosti; u suprotnom, morate promijeniti predznak nejednakosti.

Kao rezultat, dobijamo nejednakost:

Sada predstavljamo lijevoj strani na oblik jednačine jednak nuli. Umjesto znaka “manje od” stavljamo “jednako” i rješavamo jednačinu. Tako ćemo pronaći ODZ. Nadamo se da ćemo sa rješenjem za ovo jednostavna jednačina nećete imati nikakvih problema. Odgovori su -4 i -2. To nije sve. Ove tačke morate prikazati na grafikonu, stavljajući “+” i “-”. Šta treba učiniti za ovo? Zamijenite brojeve iz intervala u izraz. Gdje su vrijednosti pozitivne, stavljamo "+".

Odgovori: x ne može biti veći od -4 i manji od -2.

Pronašli smo raspon prihvatljivih vrijednosti samo za lijevu stranu, sada moramo pronaći raspon prihvatljivih vrijednosti za desnu stranu. Ovo je mnogo lakše. Odgovor: -2. Presijecamo oba rezultirajuća područja.

I tek sada počinjemo da se bavimo samom nejednakošću.

Pojednostavimo ga što je više moguće kako bismo ga lakše riješili.

Ponovo koristimo metodu intervala u rješenju. Preskočimo kalkulacije s tim je već sve jasno iz prethodnog primjera. Odgovori.

Ali ova metoda je prikladna ako logaritamska nejednakost ima iste baze.

Rješavanje logaritamskih jednadžbi i nejednačina sa iz različitih razloga pretpostavlja početno svođenje na jednu bazu. Zatim koristite metodu opisanu gore. Ali ima još toga težak slučaj. Razmotrimo jednu od najbrojnijih složene vrste logaritamske nejednakosti.

Logaritamske nejednakosti sa promenljivom bazom

Kako riješiti nejednakosti sa takvim karakteristikama? Da, i takvi se ljudi mogu naći na Jedinstvenom državnom ispitu. Rješavanje nejednačina na sljedeći način također će vam koristiti obrazovni proces. Hajde da razumemo problem detaljno. Odbacimo teoriju i pređimo odmah na praksu. Za rješavanje logaritamskih nejednakosti dovoljno je jednom se upoznati s primjerom.

Za rješavanje logaritamske nejednakosti prikazanog oblika potrebno je desnu stranu svesti na logaritam s istom osnovom. Princip liči na ekvivalentne prelaze. Kao rezultat, nejednakost će izgledati ovako.

Zapravo, ostaje samo da se napravi sistem nejednakosti bez logaritama. Koristeći metodu racionalizacije, prelazimo na ekvivalentan sistem nejednakosti. Shvatit ćete samo pravilo kada zamijenite odgovarajuće vrijednosti i pratite njihove promjene. Sistem će imati sljedeće nejednakosti.

Kada koristite metodu racionalizacije pri rješavanju nejednakosti, morate zapamtiti sljedeće: jedan se mora oduzeti od baze, x, po definiciji logaritma, oduzima se od obje strane nejednakosti (desno slijeva), dva izraza se množe i postavljen pod originalnim predznakom u odnosu na nulu.

Dalje rješenje se provodi metodom intervala, ovdje je sve jednostavno. Važno je da shvatite razlike u metodama rješenja, tada će sve početi lako funkcionirati.

Postoje mnoge nijanse u logaritamskim nejednačinama. Najjednostavnije od njih je prilično lako riješiti. Kako možete riješiti svaki od njih bez problema? Već ste dobili sve odgovore u ovom članku. Sada je pred vama duga praksa. Konstantno vježbajte rješavanje najviše različite zadatke u okviru ispita i moći ćete da dobijete najviši rezultat. Sretno u Vašem teškom zadatku!

Među čitavom raznolikošću logaritamskih nejednakosti posebno se proučavaju nejednakosti sa promjenjivom bazom. Oni se rješavaju pomoću posebne formule, koja se iz nekog razloga rijetko uči u školi:

log k (x) f (x) ∨ log k (x) g (x) ⇒ (f (x) − g (x)) (k (x) − 1) ∨ 0

Umjesto “∨” polja za potvrdu možete staviti bilo koji znak nejednakosti: više ili manje. Glavna stvar je da su u obje nejednakosti predznaci isti.

Na ovaj način se rješavamo logaritama i problem svodimo na racionalna nejednakost. Potonje je mnogo lakše riješiti, ali pri odbacivanju logaritma mogu se pojaviti dodatni korijeni. Da biste ih odsjekli, dovoljno je pronaći raspon prihvatljivih vrijednosti. Ako ste zaboravili ODZ logaritma, toplo preporučujem da ga ponovite - pogledajte “Šta je logaritam”.

Sve što se odnosi na raspon prihvatljivih vrijednosti mora se posebno zapisati i riješiti:

f(x) > 0; g(x) > 0; k(x) > 0; k(x) ≠ 1.

Ove četiri nejednakosti čine sistem i moraju biti zadovoljene istovremeno. Kada je raspon prihvatljivih vrijednosti pronađen, ostaje samo da ga presječemo rješenjem racionalne nejednakosti - i odgovor je spreman.

Zadatak. Riješite nejednačinu:

Prvo, napišimo ODZ logaritma:

Prve dvije nejednakosti su zadovoljene automatski, ali će posljednja morati biti ispisana. Pošto je kvadrat broja nula ako i samo ako je sam broj nula, imamo:

x 2 + 1 ≠ 1;
x 2 ≠ 0;
x ≠ 0.

Ispada da su ODZ logaritma svi brojevi osim nule: x ∈ (−∞ 0)∪(0; +∞). Sada rješavamo glavnu nejednakost:

Vršimo prijelaz sa logaritamske nejednakosti na racionalnu. Izvorna nejednakost ima predznak “manje od”, što znači da rezultirajuća nejednakost također mora imati predznak “manje od”. imamo:

(10 − (x 2 + 1)) · (x 2 + 1 − 1)< 0;
(9 − x 2) x 2< 0;
(3 − x) · (3 + x) · x 2< 0.

Nule ovog izraza su: x = 3; x = −3; x = 0. Štaviše, x = 0 je korijen drugog višestrukosti, što znači da se pri prolasku kroz njega predznak funkcije ne mijenja. imamo:

Dobijamo x ∈ (−∞ −3)∪(3; +∞). Ovaj set je u potpunosti sadržan u ODZ-u logaritma, što znači da je ovo odgovor.

Pretvaranje logaritamskih nejednakosti

Često je originalna nejednakost drugačija od gornje. Ovo se lako može ispraviti korištenjem standardnih pravila za rad s logaritmima - pogledajte “Osnovna svojstva logaritma”. naime:

1. Bilo koji broj se može predstaviti kao logaritam sa datom bazom;
2. Zbir i razlika logaritama sa istim bazama mogu se zamijeniti jednim logaritmom.

Zasebno, želio bih vas podsjetiti na raspon prihvatljivih vrijednosti. Budući da u izvornoj nejednakosti može biti nekoliko logaritama, potrebno je pronaći VA svakog od njih. dakle, opšta šema rješenja logaritamskih nejednakosti su sljedeća:

1. Pronađite VA svakog logaritma uključenog u nejednakost;
2. Nejednakost svesti na standardnu ​​koristeći formule za sabiranje i oduzimanje logaritama;
3. Riješi rezultirajuću nejednačinu koristeći gornju shemu.

Zadatak. Riješite nejednačinu:

Nađimo domen definicije (DO) prvog logaritma:

Rješavamo metodom intervala. Pronalaženje nula brojilaca:

3x − 2 = 0;
x = 2/3.

Zatim - nule imenioca:

x − 1 = 0;
x = 1.

Na koordinatnoj strelici označavamo nule i znakove:

Dobijamo x ∈ (−∞ 2/3)∪(1; +∞). Drugi logaritam će imati isti VA. Ako mi ne vjerujete, možete provjeriti. Sada transformiramo drugi logaritam tako da je baza dva:

Kao što vidite, trojke u osnovi i ispred logaritma su smanjene. Dobili smo dva logaritma sa istom bazom. Hajde da ih zbrojimo:

log 2 (x − 1) 2< 2;
log 2 (x − 1) 2< log 2 2 2 .

Dobili smo standardnu ​​logaritamsku nejednakost. Riješimo se logaritama pomoću formule. Budući da izvorna nejednakost sadrži znak “manje od”, rezultirajuća racionalno izražavanje također mora biti manji od nule. imamo:

(f (x) − g (x)) (k (x) − 1)< 0;
((x − 1) 2 − 2 2) (2 − 1)< 0;
x 2 − 2x + 1 − 4< 0;
x 2 − 2x − 3< 0;
(x − 3)(x + 1)< 0;
x ∈ (−1; 3).

Imamo dva seta:

1. ODZ: x ∈ (−∞ 2/3)∪(1; +∞);
2. Odgovor kandidata: x ∈ (−1; 3).

Ostaje presijecati ove skupove - dobijamo pravi odgovor:

Zanima nas presjek skupova, pa biramo intervale koji su zasjenjeni na obje strelice. Dobijamo x ∈ (−1; 2/3)∪(1; 3) - sve tačke su izbušene.

Definicija logaritma Najlakši način da to napišete matematički je:

Definicija logaritma se može napisati na drugi način:

Obratite pažnju na ograničenja koja su nametnuta bazi logaritma ( a) i na sublogaritamski izraz ( x). U budućnosti će se ovi uvjeti pretvoriti u važna ograničenja za OD, koja će se morati uzeti u obzir pri rješavanju bilo koje jednadžbe sa logaritmima. Dakle, sada, pored standardnih uslova koji dovode do ograničenja na ODZ (pozitivnost izraza pod korenima parnih stepena, nejednak imenilac nuli, itd.), moraju se uzeti u obzir i sledeći uslovi:

• Sublogaritamski izraz može biti samo pozitivan.
• Osnova logaritma može biti samo pozitivna, a ne jednaka jedinici.

Imajte na umu da ni osnova logaritma ni podlogaritamski izraz ne mogu biti jednaki nuli. Također imajte na umu da sama vrijednost logaritma može poprimiti sve moguće vrijednosti, tj. Logaritam može biti pozitivan, negativan ili nula. Logaritama ima mnogo razna svojstva, koji proizlaze iz svojstava potencija i definicije logaritma. Hajde da ih navedemo. Dakle, svojstva logaritama:

Logaritam proizvoda:

Logaritam razlomka:

Izuzimanje stepena iz predznaka logaritma:

Posebno obratite pažnju na one od posljednjih navedenih svojstava u kojima se znak modula pojavljuje nakon uzimanja stepena. Ne zaboravite da kada stavljate parni stepen izvan znaka logaritma, ispod logaritma ili na osnovu, morate ostaviti znak modula.

Ostalo korisna svojstva logaritmi:

Posljednje svojstvo se vrlo često koristi u složenim logaritamskim jednačinama i nejednačinama. Treba ga pamtiti kao i sve ostale, iako se često zaboravlja.

Najjednostavnije logaritamske jednadžbe izgledaju ovako:

A njihovo rješenje je dato formulom koja direktno slijedi iz definicije logaritma:

Druge najjednostavnije logaritamske jednadžbe su one koje se, korištenjem algebarskih transformacija i gornjih formula i svojstava logaritama, mogu svesti na oblik:

Rješenje takvih jednačina uzimajući u obzir ODZ je sljedeće:

Neki drugi logaritamske jednadžbe s promjenljivom u osnovi može se svesti na oblik:

U takvim logaritamskim jednačinama opšti pogled rješenje također slijedi direktno iz definicije logaritma. Samo u ovom slučaju postoje dodatna ograničenja za DZ koja treba uzeti u obzir. Kao rezultat toga, da biste riješili logaritamsku jednadžbu s promjenljivom u bazi, morate riješiti sljedeći sistem:

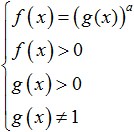
Prilikom rješavanja složenijih logaritamskih jednadžbi koje se ne mogu svesti na jednu od gore predstavljenih jednačina, također se aktivno koristi varijabilna metoda zamjene. Kao i obično, kada koristite ovu metodu, morate imati na umu da nakon uvođenja zamjene, jednadžba bi trebala biti pojednostavljena i više ne sadrži staru nepoznatu. Također morate zapamtiti da izvršite obrnutu zamjenu varijabli.

Ponekad pri rješavanju logaritamskih jednadžbi također morate koristiti grafička metoda . Ova metoda sastoji se u tome da se što preciznije na jednoj koordinatnoj ravni konstruišu grafovi funkcija koji se nalaze na levoj i desnoj strani jednačine, a zatim se sa crteža pronađu koordinate njihovih presečnih tačaka. Korijeni dobiveni na ovaj način moraju se provjeriti zamjenom u originalnu jednačinu.

Prilikom rješavanja logaritamskih jednačina često je također korisno metod grupisanja. Kada koristite ovu metodu, glavna stvar koju treba zapamtiti je da: da bi proizvod nekoliko faktora bio jednak nuli, potrebno je da barem jedan od njih bude jednak nuli, a ostalo je postojalo. Kada su faktori logaritmi ili zagrade sa logaritmima, a ne samo zagrade sa varijablama kao u racionalne jednačine, tada se mogu pojaviti mnoge greške. Budući da logaritmi imaju mnoga ograničenja na regiju u kojoj postoje.

Prilikom odlučivanja sistemi logaritamskih jednačina Najčešće morate koristiti ili metodu zamjene ili metodu zamjene varijable. Ako postoji takva mogućnost, onda se pri rješavanju sistema logaritamskih jednačina mora nastojati osigurati da se svaka od jednačina sistema pojedinačno dovede u oblik u kojem će biti moguć prijelaz iz logaritamske jednačine u racionalan.

Najjednostavnije logaritamske nejednačine rješavaju se na približno isti način kao i slične jednadžbe. Prvo, koristeći algebarske transformacije i svojstva logaritama, moramo pokušati da ih dovedemo do oblika u kojem će logaritmi na lijevoj i desnoj strani nejednačine imati iste osnove, tj. dobiti nejednakost oblika:

Nakon toga morate prijeći na racionalnu nejednakost, uzimajući u obzir da ovaj prijelaz treba izvesti na sljedeći način: ako je osnova logaritma veća od jedan, tada se ne treba mijenjati znak nejednakosti, a ako je baza logaritma je manja od jedan, tada trebate promijeniti predznak nejednakosti u suprotan (to znači promjenu "manje" u "više" ili obrnuto). U ovom slučaju, nema potrebe mijenjati znake minus u plus jedan, zaobilazeći prethodno naučena pravila. Zapišimo matematički šta smo dobili kao rezultat izvođenja takvog prijelaza. Ako je baza veća od jedan dobijamo:

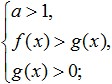
Ako je osnova logaritma manja od jedan, mijenjamo predznak nejednakosti i dobijamo sljedeći sistem:

Kao što vidimo, pri rješavanju logaritamskih nejednačina, kao i obično, uzima se u obzir i ODZ (ovo je treći uvjet u gornjim sistemima). Štaviše, u ovom slučaju moguće je ne zahtijevati pozitivnost oba podlogaritamska izraza, već zahtijevati pozitivnost samo manjeg od njih.

Prilikom odlučivanja logaritamske nejednakosti sa promenljivom u osnovi logaritma, potrebno je samostalno razmotriti obje opcije (kada je baza manja od jedan, a veća od jedan) i spojiti rješenja ovih slučajeva u skup. Istovremeno, ne smijemo zaboraviti na DL, tj. o činjenici da i baza i svi podlogaritamski izrazi moraju biti pozitivni. Dakle, pri rješavanju nejednakosti oblika:

Dobijamo sledeći set sistema:

Složenije logaritamske nejednakosti također se mogu riješiti korištenjem promjena varijabli. Neke druge logaritamske nejednačine (kao i logaritamske jednačine) zahtijevaju rješavanje postupka uzimanja logaritma obje strane nejednačine ili jednačine. istu osnovu. Dakle, kada se provodi takav postupak s logaritamskim nejednakostima, postoji suptilnost. Imajte na umu da kada se logaritmi uzimaju na bazu veću od jedan, predznak nejednakosti se ne mijenja, ali ako je baza manja od jedan, onda se predznak nejednakosti obrće.

Ako se logaritamska nejednakost ne može svesti na racionalnu ili riješiti zamjenom, tada se u ovom slučaju mora koristiti metoda generalizovanog intervala, što je kako slijedi:

• Define DL;
• Transformirajte nejednakost tako da na desnoj strani bude nula (na lijevoj strani, ako je moguće, smanjite na zajednički imenilac, faktorizacija, itd.);
• Pronađite sve korijene brojnika i nazivnika i ucrtajte ih na brojevnu osu, a ako nejednakost nije stroga, prebojite korijene brojnika, ali u svakom slučaju ostavite korijene nazivnika iscrtane;
• Pronađite predznak cijelog izraza na svakom od intervala zamjenom broja iz datog intervala u transformiranu nejednačinu. U tom slučaju više nije moguće mijenjati znakove na bilo koji način pri prolasku kroz točke na osi. Potrebno je odrediti predznak izraza na svakom intervalu zamjenom vrijednosti iz intervala u ovaj izraz, i tako dalje za svaki interval. Nema drugog načina (o tome se radi, uglavnom, razlika između metode generaliziranog intervala i uobičajene);
• Pronađite presjek ODZ-a i intervala koji zadovoljavaju nejednakost, ali ne gubite pojedinačne točke koje zadovoljavaju nejednakost (korijene brojnika u nestrogim nejednačinama), i ne zaboravite iz odgovora isključiti sve korijene imenilac u svim nejednačinama.

• Nazad
• Naprijed

Kako se uspješno pripremiti za CT iz fizike i matematike?

Da bi se uspješno pripremili za CT iz fizike i matematike, između ostalog, potrebno je ispuniti tri najvažnija uslova:

1. Proučite sve teme i ispunite sve testove i zadatke date u edukativnim materijalima na ovoj stranici. Da biste to učinili, ne trebate baš ništa, naime: svaki dan posvetite tri do četiri sata pripremi za CT iz fizike i matematike, proučavanju teorije i rješavanju problema. Činjenica je da je CT ispit na kojem nije dovoljno samo znati fiziku ili matematiku, potrebno ga je i riješiti brzo i bez grešaka veliki broj zadaci za različite teme I različite složenosti. Ovo poslednje se može naučiti samo rešavanjem hiljada problema.
2. Naučite sve formule i zakone u fizici, te formule i metode u matematici. U stvari, ovo je takođe vrlo jednostavno za napraviti, potrebne formule u fizici ima svega oko 200 komada, a u matematici još nešto manje. Svaki od ovih predmeta ima desetak standardnih metoda za rješavanje problema osnovni nivo poteškoće koje se takođe mogu naučiti, a samim tim potpuno automatski i bez poteškoća pravi trenutak većina DH. Nakon toga, morat ćete razmišljati samo o najtežim zadacima.
3. Pohađati sve tri faze probnog testiranja iz fizike i matematike. Svaki RT se može posjetiti dva puta da se odluči za obje opcije. Opet, na CT-u, pored sposobnosti brzog i efikasnog rješavanja problema, te poznavanja formula i metoda, morate znati i pravilno planirati vrijeme, rasporediti snage, i što je najvažnije, pravilno popuniti formular za odgovore, bez zbunjujući brojeve odgovora i zadataka, ili svoje prezime. Takođe, tokom RT-a, važno je naviknuti se na stil postavljanja pitanja u problemima, što se nespremnoj osobi u DT-u može učiniti vrlo neuobičajenim.

Uspješna, marljiva i odgovorna primjena ove tri tačke omogućit će vam da se pojavite na CT-u odličan rezultat, maksimum onoga za šta ste sposobni.

Našli ste grešku?

Ako mislite da ste pronašli grešku u edukativni materijali, a zatim pišite o tome putem e-pošte. Takođe možete prijaviti grešku društvena mreža(). U pismu naznačite predmet (fizika ili matematika), naziv ili broj teme ili testa, broj zadatka ili mjesto u tekstu (stranici) na kojem, po vašem mišljenju, postoji greška. Također opišite o čemu se sumnja na grešku. Vaše pismo neće proći nezapaženo, greška će biti ili ispravljena, ili će Vam biti objašnjeno zašto nije greška.

Očuvanje vaše privatnosti nam je važno. Iz tog razloga smo razvili Politiku privatnosti koja opisuje kako koristimo i pohranjujemo vaše podatke. Pregledajte našu praksu privatnosti i javite nam ako imate pitanja.

Prikupljanje i korištenje ličnih podataka

Lični podaci odnose se na podatke koji se mogu koristiti za identifikaciju ili kontaktiranje određene osobe.

Od vas se može tražiti da unesete svoje lične podatke u bilo koje vrijeme kada nas kontaktirate.

U nastavku su navedeni neki primjeri vrsta ličnih podataka koje možemo prikupljati i kako ih možemo koristiti.

Koje lične podatke prikupljamo:

• Kada podnesete zahtjev na web stranici, možemo prikupiti različite informacije, uključujući vaše ime, broj telefona, adresu email itd.

Kako koristimo vaše lične podatke:

• Prikupljeno od nas lične podatke omogućava nam da vas kontaktiramo i informiramo o jedinstvenim ponudama, promocijama i drugim događajima i nadolazećim događajima.
• S vremena na vrijeme možemo koristiti vaše lične podatke za slanje važnih obavijesti i komunikacija.
• Također možemo koristiti lične podatke za interne svrhe kao što su revizija, analiza podataka i razne studije kako bismo poboljšali usluge koje pružamo i dali vam preporuke u vezi s našim uslugama.
• Ako učestvujete u nagradnoj igri, natjecanju ili sličnoj promociji, možemo koristiti informacije koje nam date za upravljanje takvim programima.

Otkrivanje informacija trećim licima

Podatke koje dobijemo od vas ne otkrivamo trećim licima.

Izuzeci:

• Po potrebi, u skladu sa zakonom, sudski postupak, V suđenje, i/ili na osnovu javnih zahtjeva ili zahtjeva od vladine agencije na teritoriji Ruske Federacije - otkrijte svoje lične podatke. Također možemo otkriti informacije o vama ako utvrdimo da je takvo otkrivanje neophodno ili prikladno za sigurnosne, provođenje zakona ili druge svrhe javnog zdravlja. važnim slučajevima.
• U slučaju reorganizacije, spajanja ili prodaje, možemo prenijeti lične podatke koje prikupimo na odgovarajuću treću stranu.

Zaštita ličnih podataka

Poduzimamo mjere opreza - uključujući administrativne, tehničke i fizičke - da zaštitimo vaše osobne podatke od gubitka, krađe i zloupotrebe, kao i neovlaštenog pristupa, otkrivanja, izmjene i uništenja.

Poštivanje vaše privatnosti na nivou kompanije

Kako bismo osigurali da su vaši lični podaci sigurni, našim zaposlenima prenosimo standarde privatnosti i sigurnosti i striktno provodimo praksu privatnosti.

Logaritamske nejednakosti

U prethodnim lekcijama smo se upoznali sa logaritamskim jednadžbama i sada znamo šta su i kako ih riješiti. Današnja lekcija će biti posvećena proučavanju logaritamskih nejednakosti. Koje su to nejednakosti i koja je razlika između rješavanja logaritamske jednadžbe i nejednakosti?

Logaritamske nejednakosti- to su nejednačine koje imaju varijablu pod znakom logaritma ili u njegovoj osnovi.

Ili, također možemo reći da je logaritamska nejednačina nejednakost u kojoj će se njena nepoznata vrijednost, kao u logaritamskoj jednadžbi, pojaviti pod znakom logaritma.

Najjednostavnije logaritamske nejednakosti imaju sljedeći oblik:

gdje su f(x) i g(x) neki izrazi koji zavise od x.

Pogledajmo ovo koristeći ovaj primjer: f(x)=1+2x+x2, g(x)=3x−1.

Rješavanje logaritamskih nejednačina

Prije rješavanja logaritamskih nejednačina, vrijedi napomenuti da su kada su riješene slične eksponencijalne nejednakosti, naime:

Prvo, kada prelazimo sa logaritma na izraze pod znakom logaritma, takođe treba da uporedimo bazu logaritma sa jedinicom;

Drugo, kada rješavamo logaritamsku nejednakost korištenjem promjene varijabli, moramo rješavati nejednakosti s obzirom na promjenu dok ne dobijemo najjednostavniju nejednakost.

Ali vi i ja smo razmatrali slične aspekte rješavanja logaritamskih nejednačina. Sada obratimo pažnju na prilično značajnu razliku. Ti i ja to znamo logaritamska funkcija ima ograničeno područje definicije, dakle, prelazeći s logaritama na izraze pod znakom logaritma, morate uzeti u obzir raspon dopuštenih vrijednosti (APV).

Odnosno, to treba uzeti u obzir prilikom odlučivanja logaritamska jednačina Ti i ja možemo prvo pronaći korijene jednadžbe, a zatim provjeriti ovo rješenje. Ali rješavanje logaritamske nejednakosti neće funkcionirati na ovaj način, jer će pri prelasku s logaritama na izraze pod predznakom logaritma biti potrebno zapisati ODZ nejednakosti.

Osim toga, vrijedi zapamtiti da se teorija nejednakosti sastoji od realnih brojeva, koji su pozitivni i negativni brojevi, kao i broj 0.

Na primjer, kada je broj “a” pozitivan, tada trebate koristiti sljedeću notaciju: a >0. U ovom slučaju, i zbir i proizvod ovih brojeva također će biti pozitivni.

Glavni princip rješavanja nejednakosti je zamijeniti je jednostavnijom nejednakošću, ali glavno je da je ona ekvivalentna datoj. Nadalje, također smo dobili nejednakost i ponovo je zamijenili onom koja ima jednostavniji oblik, itd.

Prilikom rješavanja nejednakosti s promjenljivom, potrebno je pronaći sva njena rješenja. Ako dvije nejednačine imaju istu varijablu x, onda su takve nejednakosti ekvivalentne, pod uslovom da se njihova rješenja poklapaju.

Prilikom izvođenja zadataka na rješavanju logaritamskih nejednačina, morate imati na umu da kada je a > 1, tada se logaritamska funkcija povećava, a kada je 0< a < 1, то такая функция имеет свойство убывать. Эти свойства вам будут необходимы при решении логарифмических неравенств, поэтому вы их должны хорошо знать и помнить.

Metode rješavanja logaritamskih nejednačina

Pogledajmo sada neke od metoda koje se primjenjuju pri rješavanju logaritamskih nejednačina. Radi boljeg razumijevanja i asimilacije, pokušat ćemo ih razumjeti na konkretnim primjerima.

Svi znamo da najjednostavnija logaritamska nejednakost ima sljedeći oblik:

U ovoj nejednakosti, V – je jedan od sljedećih znakova nejednakosti:<,>, ≤ ili ≥.

Kada je baza datog logaritma veća od jedan (a>1), čineći prijelaz sa logaritama na izraze pod predznakom logaritma, tada je u ovoj verziji znak nejednakosti sačuvan, a nejednakost će imati sljedeći oblik:

što je ekvivalentno ovom sistemu:

U slučaju kada je osnova logaritma veća od nule i manja od jedan (0

Ovo je ekvivalentno ovom sistemu:

Pogledajmo još primjera rješavanja najjednostavnijih logaritamskih nejednačina prikazanih na slici ispod:

Primjeri rješavanja

Vježbajte. Pokušajmo riješiti ovu nejednakost:

Rješavanje raspona prihvatljivih vrijednosti.

Pokušajmo sada pomnožiti njegovu desnu stranu sa:

Hajde da vidimo šta možemo da smislimo:

Sada, pređimo na pretvaranje podlogaritamskih izraza. Zbog činjenice da je osnova logaritma 0< 1/4 <1, то от сюда следует, что знак неравенства изменится на противоположный:

3x - 8 > 16;
3x > 24;
x > 8.

A iz ovoga proizilazi da interval koji smo dobili u potpunosti pripada ODZ-u i da je rješenje takve nejednakosti.

Evo odgovora koji smo dobili:

Šta je potrebno za rješavanje logaritamskih nejednakosti?

Pokušajmo sada analizirati šta nam je potrebno za uspješno rješavanje logaritamskih nejednakosti?

Prvo, koncentrišite svu svoju pažnju i pokušajte da ne pogrešite kada izvodite transformacije koje su date u ovoj nejednakosti. Također, treba imati na umu da je prilikom rješavanja ovakvih nejednačina potrebno izbjegavati proširenja i kontrakcije nejednačina, što može dovesti do gubitka ili sticanja stranih rješenja.

Drugo, kada rješavate logaritamske nejednakosti, morate naučiti logično razmišljati i razumjeti razliku između pojmova kao što su sistem nejednakosti i skup nejednakosti, tako da možete lako odabrati rješenja nejednakosti, a pritom se voditi njenim DL.

Treće, da biste uspješno riješili takve nejednakosti, svako od vas mora savršeno poznavati sva svojstva elementarne funkcije i jasno razumeju njihovo značenje. Takve funkcije uključuju ne samo logaritamske, već i racionalne, stepene, trigonometrijske, itd., jednom riječju, sve one koje ste proučavali tijekom školovanje algebra.

Kao što vidite, nakon što ste proučili temu logaritamskih nejednakosti, nema ništa teško u rješavanju ovih nejednakosti, pod uvjetom da ste pažljivi i uporni u postizanju svojih ciljeva. Da biste izbjegli bilo kakve probleme u rješavanju nejednakosti, potrebno je što više vježbati, rješavajući različite zadatke i pritom zapamtiti osnovne metode rješavanja takvih nejednačina i njihovih sistema. Ako ne uspete da rešite logaritamske nejednakosti, trebalo bi da pažljivo analizirate svoje greške kako se ne biste više vraćali na njih u budućnosti.

Domaći

Da biste bolje razumjeli temu i konsolidirali obrađeni materijal, riješite sljedeće nejednakosti: