Koja funkcija se zove parna i neparna. Studija funkcije
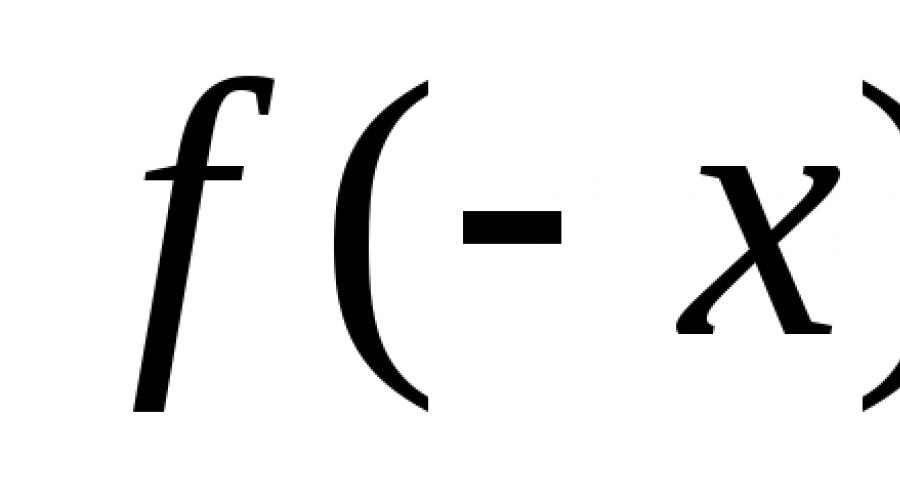
Pročitajte također
Parnost i neparnost funkcije su jedno od njenih glavnih svojstava, a parnost zauzima impresivnu ulogu školski kurs matematike. U velikoj mjeri određuje ponašanje funkcije i uvelike olakšava konstrukciju odgovarajućeg grafa.
Odredimo parnost funkcije. Općenito govoreći, proučavana funkcija se smatra čak i ako se za suprotne vrijednosti nezavisne varijable (x) koja se nalazi u njenoj domeni definicije, odgovarajuće vrijednosti y (funkcija) pokažu jednake.
Hajde da damo strožiju definiciju. Razmotrimo neku funkciju f (x), koja je definirana u domeni D. To će biti čak i ako za bilo koju tačku x koja se nalazi u domeni definicije:
- -x (suprotna tačka) takođe leži u ovom opsegu,
- f(-x) = f(x).
Iz gornje definicije slijedi uslov neophodan za domenu definicije takve funkcije, naime, simetrija u odnosu na tačku O, koja je ishodište koordinata, jer ako je neka tačka b sadržana u domeni definicije parnog funkcija, tada odgovarajuća tačka b takođe leži u ovom domenu. Iz navedenog, dakle, slijedi sljedeći zaključak: ravnomjerna funkcija ima simetričan izgled u odnosu na os ordinate (Oy).
Kako odrediti paritet funkcije u praksi?
Neka se specificira pomoću formule h(x)=11^x+11^(-x). Prateći algoritam koji slijedi direktno iz definicije, prvo ispitujemo njen domen definicije. Očigledno je definiran za sve vrijednosti argumenta, odnosno, prvi uvjet je zadovoljen.
Sljedeći korak je zamjena suprotne vrijednosti (-x) za argument (x).
Dobijamo:
h(-x) = 11^(-x) + 11^x.
Pošto sabiranje zadovoljava komutativni (komutativni) zakon, očito je da je h(-x) = h(x) i dato funkcionalna zavisnost- čak.
Provjerimo parnost funkcije h(x)=11^x-11^(-x). Prateći isti algoritam, dobijamo da je h(-x) = 11^(-x) -11^x. Uzimajući minus, na kraju imamo
h(-x)=-(11^x-11^(-x))=- h(x). Dakle, h(x) je neparan.
Usput, treba podsjetiti da postoje funkcije koje se ne mogu klasificirati prema ovim kriterijima, ne nazivaju se ni parnim ni neparnim.
Čak i funkcije imaju niz zanimljivih svojstava:
- kao rezultat dodavanja sličnih funkcija, dobijaju parnu;
- kao rezultat oduzimanja takvih funkcija, dobiva se paran;
- čak, takođe čak;
- kao rezultat množenja dvije takve funkcije, dobiva se parna;
- kao rezultat množenja neparnih i parnih funkcija, dobiva se neparna;
- kao rezultat dijeljenja neparnih i parnih funkcija, dobiva se neparna;
- derivacija takve funkcije je neparna;
- Ako kvadrirate neparnu funkciju, dobit ćete parnu funkciju.
Parnost funkcije može se koristiti za rješavanje jednačina.
Za rješavanje jednačine kao što je g(x) = 0, gdje je lijeva strana jednadžba je parna funkcija, bit će sasvim dovoljno pronaći njena rješenja za nenegativne vrijednosti varijable. Dobiveni korijeni jednadžbe moraju se kombinirati sa suprotnim brojevima. Jedan od njih podliježe verifikaciji.
Ovo se također uspješno koristi za rješavanje nestandardni zadaci sa parametrom.
Na primjer, postoji li neka vrijednost parametra a za koju će jednačina 2x^6-x^4-ax^2=1 imati tri korijena?
Ako uzmemo u obzir da varijabla ulazi u jednačinu po parnim potencijama, onda je jasno da zamjena x sa - x zadata jednačina neće se promeniti. Iz toga slijedi da ako je određeni broj njegov korijen, onda je i suprotni broj korijen. Zaključak je očigledan: korijeni jednadžbe koji se razlikuju od nule uključeni su u skup njenih rješenja u „parovima“.
Jasno je da sam broj nije 0, odnosno da broj korijena takve jednadžbe može biti samo paran i, naravno, za bilo koju vrijednost parametra ne može imati tri korijena.
Ali broj korijena jednačine 2^x+ 2^(-x)=ax^4+2x^2+2 može biti neparan i za bilo koju vrijednost parametra. Zaista, lako je provjeriti da skup korijena ove jednadžbe sadrži rješenja “u parovima”. Provjerimo da li je 0 korijen. Kada ga zamenimo u jednačinu, dobijamo 2=2. Dakle, pored „sparenih“ 0 je i koren, što dokazuje njihov neparni broj.
Ravnomjerna funkcija.
Čak je funkcija čiji se predznak ne mijenja kada se predznak promijeni x.
x jednakost važi f(–x) = f(x). Potpiši x ne utiče na znak y.
Grafikon parne funkcije je simetričan u odnosu na koordinatnu os (slika 1).
Primjeri parne funkcije:
y=cos x
y = x 2
y = –x 2
y = x 4
y = x 6
y = x 2 + x
Objašnjenje:
Uzmimo funkciju y = x 2 ili y = –x 2 .
Za bilo koju vrijednost x funkcija je pozitivna. Potpiši x ne utiče na znak y. Grafikon je simetričan u odnosu na koordinatnu os. Ovo je ravnomjerna funkcija.
Neparna funkcija.
Odd je funkcija čiji se predznak mijenja kada se predznak promijeni x.
Drugim riječima, za bilo koju vrijednost x jednakost važi f(–x) = –f(x).
Grafikon neparne funkcije je simetričan u odnosu na ishodište (slika 2).
Primjeri neparnih funkcija:
y= grijeh x
y = x 3
y = –x 3
Objašnjenje:
Uzmimo funkciju y = – x 3 .
Sva značenja at imaće znak minus. To je znak x utiče na znak y. Ako je nezavisna varijabla pozitivan broj, onda je funkcija pozitivna, ako je nezavisna varijabla negativan broj, tada je funkcija negativna: f(–x) = –f(x).
Grafikon funkcije je simetričan u odnosu na ishodište. Ovo je čudna funkcija.
Svojstva parnih i neparnih funkcija:
BILJEŠKA:
Nisu sve funkcije parne ili neparne. Postoje funkcije koje se ne povinuju takvoj gradaciji. Na primjer, root funkcija at = √X ne odnosi se ni na parne ni neparne funkcije (slika 3). Prilikom navođenja svojstava takvih funkcija treba dati odgovarajući opis: ni par ni neparan.
Kao što znate, periodičnost je ponavljanje određenih procesa u određenom intervalu. Pozivaju se funkcije koje opisuju ove procese periodične funkcije. Odnosno, to su funkcije u čijim grafovima postoje elementi koji se ponavljaju u određenim numeričkim intervalima.
Funkcija se naziva parna (neparna) ako je za bilo koji i jednakost 
 .
.
Grafikon parne funkcije je simetričan u odnosu na os  .
.
Graf neparne funkcije je simetričan u odnosu na ishodište.
Primjer 6.2. Ispitajte je li funkcija parna ili neparna
1)
 ;
2)
;
2) ;
3)
;
3) .
.
Rješenje.
1) Funkcija je definirana kada  . Naći ćemo
. Naći ćemo  .
.
One.  . znači, ovu funkciju je čak.
. znači, ovu funkciju je čak.
2) Funkcija je definirana kada 
One.  . Dakle, ova funkcija je čudna.
. Dakle, ova funkcija je čudna.
3) funkcija je definirana za , tj. Za
 ,
,
 . Stoga funkcija nije ni parna ni neparna. Nazovimo to funkcijom općeg oblika.
. Stoga funkcija nije ni parna ni neparna. Nazovimo to funkcijom općeg oblika.
3. Proučavanje funkcije za monotonost.
Funkcija  naziva se povećanjem (opadanjem) na određenom intervalu ako je u tom intervalu svaki veća vrijednost argument odgovara većoj (manjoj) vrijednosti funkcije.
naziva se povećanjem (opadanjem) na određenom intervalu ako je u tom intervalu svaki veća vrijednost argument odgovara većoj (manjoj) vrijednosti funkcije.
Funkcije koje rastu (opadaju) u određenom intervalu nazivaju se monotonim.
Ako je funkcija  diferencibilan na intervalu
diferencibilan na intervalu  i ima pozitivan (negativni) izvod
i ima pozitivan (negativni) izvod  , zatim funkciju
, zatim funkciju  povećava (smanjuje) u ovom intervalu.
povećava (smanjuje) u ovom intervalu.
Primjer 6.3. Naći intervale monotonosti funkcija
1)
 ;
3)
;
3) .
.
Rješenje.
1) Ova funkcija je definirana na cijeloj brojevnoj pravoj. Nađimo derivat.
Izvod je jednak nuli ako  I
I  . Domen definicije je brojevna osa, podijeljena tačkama
. Domen definicije je brojevna osa, podijeljena tačkama  ,
, u intervalima. Odredimo predznak derivacije u svakom intervalu.
u intervalima. Odredimo predznak derivacije u svakom intervalu.

U intervalu  derivacija je negativna, funkcija opada na ovom intervalu.
derivacija je negativna, funkcija opada na ovom intervalu.
U intervalu  derivacija je pozitivna, dakle, funkcija raste u ovom intervalu.
derivacija je pozitivna, dakle, funkcija raste u ovom intervalu.
2) Ova funkcija je definirana ako  ili
ili
 .
.

Određujemo predznak kvadratnog trinoma u svakom intervalu.
Dakle, domen definicije funkcije
Nađimo derivat  ,
, , Ako
, Ako  , tj.
, tj.  , Ali
, Ali  . Odredimo predznak derivacije u intervalima
. Odredimo predznak derivacije u intervalima  .
.

U intervalu  derivacija je negativna, pa se funkcija smanjuje na intervalu
derivacija je negativna, pa se funkcija smanjuje na intervalu  . U intervalu
. U intervalu  izvod je pozitivan, funkcija raste u intervalu
izvod je pozitivan, funkcija raste u intervalu  .
.
4. Proučavanje funkcije na ekstremumu.
Dot  naziva maksimalnom (minimalnom) tačkom funkcije
naziva maksimalnom (minimalnom) tačkom funkcije  , ako postoji takva okolina tačke
, ako postoji takva okolina tačke  to je za sve
to je za sve  iz ovog susjedstva vrijedi nejednakost
iz ovog susjedstva vrijedi nejednakost 
 .
.
Maksimalne i minimalne tačke funkcije nazivaju se tačke ekstrema.
Ako je funkcija  u tački
u tački  ima ekstrem, onda je derivacija funkcije u ovoj tački jednaka nuli ili ne postoji (neophodan uslov za postojanje ekstrema).
ima ekstrem, onda je derivacija funkcije u ovoj tački jednaka nuli ili ne postoji (neophodan uslov za postojanje ekstrema).
Tačke u kojima je izvod nula ili ne postoji nazivaju se kritičnim.
5. Dovoljni uslovi za postojanje ekstrema.
Pravilo 1. Ako je tokom tranzicije (s lijeva na desno) kroz kritičnu tačku  derivat
derivat  mijenja znak iz “+” u “–”, a zatim u tački
mijenja znak iz “+” u “–”, a zatim u tački  funkcija
funkcija  ima maksimum; ako je od “–” do “+”, onda minimum; Ako
ima maksimum; ako je od “–” do “+”, onda minimum; Ako  ne mijenja predznak, onda nema ekstrema.
ne mijenja predznak, onda nema ekstrema.
Pravilo 2. Neka u tački  prvi izvod funkcije
prvi izvod funkcije  jednaka nuli
jednaka nuli  , a drugi izvod postoji i razlikuje se od nule. Ako
, a drugi izvod postoji i razlikuje se od nule. Ako  , To
, To  – maksimalni bod, ako
– maksimalni bod, ako  , To
, To  – minimalna tačka funkcije.
– minimalna tačka funkcije.
Primjer 6.4 . Istražite maksimalne i minimalne funkcije:
1)
 ;
2)
;
2) ;
3)
;
3) ;
;
4)
 .
.
Rješenje.
1) Funkcija je definirana i kontinuirana na intervalu  .
.
Nađimo derivat  i riješi jednačinu
i riješi jednačinu  , tj.
, tj.  .Odavde
.Odavde  – kritične tačke.
– kritične tačke.
Odredimo predznak derivacije u intervalima ,  .
.

Prilikom prolaska kroz tačke  I
I  derivacija mijenja predznak iz “–” u “+”, dakle, prema pravilu 1
derivacija mijenja predznak iz “–” u “+”, dakle, prema pravilu 1  – minimalni bodovi.
– minimalni bodovi.
Prilikom prolaska kroz tačku  derivacija mijenja predznak iz “+” u “–”, dakle
derivacija mijenja predznak iz “+” u “–”, dakle  – maksimalni poen.
– maksimalni poen.
 ,
,
 .
.
2) Funkcija je definirana i kontinuirana u intervalu  . Nađimo derivat
. Nađimo derivat  .
.
Nakon što smo riješili jednačinu  , naći ćemo
, naći ćemo  I
I  – kritične tačke. Ako je imenilac
– kritične tačke. Ako je imenilac  , tj.
, tj.  , onda izvod ne postoji. dakle,
, onda izvod ne postoji. dakle,  – treća kritična tačka. Odredimo predznak derivacije u intervalima.
– treća kritična tačka. Odredimo predznak derivacije u intervalima.

Dakle, funkcija ima minimum u tački  , maksimum u bodovima
, maksimum u bodovima  I
I  .
.
3) Funkcija je definirana i kontinuirana ako  , tj. at
, tj. at  .
.
Nađimo derivat 
 .
.
Nađimo kritične tačke: 

Susjedstva tačaka  ne pripadaju domenu definicije, stoga nisu ekstremi. Dakle, hajde da ispitamo kritične tačke
ne pripadaju domenu definicije, stoga nisu ekstremi. Dakle, hajde da ispitamo kritične tačke  I
I  .
.

4) Funkcija je definirana i kontinuirana na intervalu  . Koristimo pravilo 2. Pronađite izvod
. Koristimo pravilo 2. Pronađite izvod  .
.
Nađimo kritične tačke:
Nađimo drugi izvod  i odredi njegov predznak u tačkama
i odredi njegov predznak u tačkama 
U tačkama  funkcija ima minimum.
funkcija ima minimum.
U tačkama  funkcija ima maksimum.
funkcija ima maksimum.
Grafovi parnih i neparnih funkcija imaju sljedeće karakteristike:
Ako je funkcija parna, tada je njen graf simetričan u odnosu na ordinatu. Ako je funkcija neparna, tada je njen graf simetričan u odnosu na ishodište.
Primjer. Konstruirajte graf funkcije \(y=\left|x \right|\).Rješenje. Razmotrite funkciju: \(f\left(x \right)=\left|x \right|\) i zamijenite suprotnu \(-x \) umjesto \(x \). Kao rezultat jednostavnih transformacija dobijamo: $$f\left(-x \right)=\left|-x \right|=\left|x \right|=f\left(x \right)$$ U drugim riječi, ako zamijenite argument suprotnim predznakom, funkcija se neće promijeniti.
To znači da je ova funkcija parna, a njen graf će biti simetričan u odnosu na ordinatnu osu ( vertikalna osa). Grafikon ove funkcije prikazan je na slici lijevo. To znači da prilikom konstruisanja grafika možete nacrtati samo polovinu, a drugi dio (lijevo od vertikalne ose, crtati simetrično na desni dio). Određivanjem simetrije funkcije prije nego što počnete crtati njen graf, možete uvelike pojednostaviti proces konstruiranja ili proučavanja funkcije. Ako je teško izvesti opću provjeru, možete to učiniti jednostavnije: zamijenite iste vrijednosti različitih predznaka u jednadžbu. Na primjer -5 i 5. Ako se ispostavi da su vrijednosti funkcije iste, onda se možemo nadati da će funkcija biti parna. Sa matematičke tačke gledišta, ovaj pristup nije sasvim ispravan, ali je s praktične tačke gledišta prikladan. Da biste povećali pouzdanost rezultata, možete zamijeniti nekoliko parova takvih suprotnih vrijednosti.
Primjer. Konstruirajte graf funkcije \(y=x\left|x \right|\).
Rješenje. Provjerimo isto kao u prethodnom primjeru: $$f\left(-x \right)=x\left|-x \right|=-x\left|x \right|=-f\left(x \right) ) $$ Ovo znači da je originalna funkcija neparna (predznak funkcije je promijenjen u suprotan).
Zaključak: funkcija je simetrična u odnosu na ishodište. Možete izgraditi samo jednu polovinu, a drugu nacrtati simetrično. Ovu vrstu simetrije je teže nacrtati. To znači da grafikon gledate s druge strane lista, pa čak i naopako. Ili možete učiniti ovo: uzmite nacrtani dio i zarotirajte ga oko ishodišta za 180 stepeni suprotno od kazaljke na satu.
Primjer. Konstruirajte graf funkcije \(y=x^3+x^2\).
Rješenje. Izvršimo istu provjeru promjene predznaka kao u prethodna dva primjera. $$f\left(-x \right)=\left(-x \right)^3+\left(-x \right)^2=-x^2+x^2$$ Kao rezultat, dobijamo to: $$f\left(-x \desno)\not=f\left(x \right),f\left(-x \right)\not=-f\left(x \right)$$ I ovo znači da funkcija nije ni parna ni neparna.
Zaključak: funkcija nije simetrična ni u odnosu na ishodište ni centar koordinatnog sistema. To se dogodilo jer je to zbir dvije funkcije: parne i neparne. Ista situacija će se dogoditi ako oduzmete dvije različite funkcije. Ali množenje ili dijeljenje će dovesti do drugačijeg rezultata. Na primjer, proizvod parne i neparne funkcije proizvodi neparnu funkciju. Ili količnik dva neparna broja vodi do parne funkcije.
Sakrij prikaz
Metode za određivanje funkcije
Neka je funkcija data formulom: y=2x^(2)-3. Dodjeljivanjem bilo koje vrijednosti nezavisnoj varijabli x, možete izračunati, koristeći ovu formulu, odgovarajuće vrijednosti zavisne varijable y. Na primjer, ako je x=-0,5, onda, koristeći formulu, nalazimo da je odgovarajuća vrijednost y y=2 \cdot (-0,5)^(2)-3=-2,5.
Uzimajući bilo koju vrijednost koju uzima argument x u formuli y=2x^(2)-3, možete izračunati samo jednu vrijednost funkcije koja joj odgovara. Funkcija se može predstaviti kao tabela:
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −4 | −3 | −2 | −1 | 0 | 1 |
Koristeći ovu tablicu, možete vidjeti da će za vrijednost argumenta −1 odgovarati vrijednost funkcije −3; a vrijednost x=2 će odgovarati y=0, itd. Također je važno znati da svaka vrijednost argumenta u tablici odgovara samo jednoj vrijednosti funkcije.
Više funkcija se može specificirati pomoću grafikona. Pomoću grafa se utvrđuje koja vrijednost funkcije korelira sa određenom vrijednošću x. Najčešće će to biti približna vrijednost funkcije.
Parna i neparna funkcija
Funkcija je ravnomjerna funkcija, kada je f(-x)=f(x) za bilo koji x iz domene definicije. Takva funkcija će biti simetrična u odnosu na Oy os.
Funkcija je neparna funkcija, kada je f(-x)=-f(x) za bilo koji x iz domene definicije. Takva funkcija će biti simetrična u odnosu na ishodište O (0;0) .
Funkcija je čak ni, ni čudno i zove se funkcija opšti pogled , kada nema simetriju u odnosu na os ili ishodište.
Hajde da ispitamo sljedeću funkciju radi pariteta:
f(x)=3x^(3)-7x^(7)
D(f)=(-\infty ; +\infty) sa simetričnim domenom definicije u odnosu na ishodište. f(-x)= 3 \cdot (-x)^(3)-7 \cdot (-x)^(7)= -3x^(3)+7x^(7)= -(3x^(3)-7x^(7))= -f(x).
To znači da je funkcija f(x)=3x^(3)-7x^(7) neparna.
Periodična funkcija
Funkcija y=f(x) , u čijoj domeni vrijedi jednakost f(x+T)=f(x-T)=f(x) za bilo koji x, naziva se periodična funkcija sa periodom T \neq 0 .
Ponavljanje grafika funkcije na bilo kojem segmentu x-ose koji ima dužinu T.
Intervali u kojima je funkcija pozitivna, odnosno f(x) > 0, su segmenti ose apscise koji odgovaraju tačkama grafa funkcije koje leže iznad ose apscise.
f(x) > 0 uključeno (x_(1); x_(2)) \cup (x_(3); +\infty)

Intervali u kojima je funkcija negativna, odnosno f(x)< 0 - отрезки оси абсцисс, которые отвечают точкам графика функции, лежащих ниже оси абсцисс.
f(x)< 0 на (-\infty; x_(1)) \cup (x_(2); x_(3))

Ograničena funkcija
Ograničeno odozdo Uobičajeno je pozvati funkciju y=f(x), x \in X kada postoji broj A za koji vrijedi nejednakost f(x) \geq A za bilo koje x \in X .
Primjer funkcije ograničene odozdo: y=\sqrt(1+x^(2)) budući da je y=\sqrt(1+x^(2)) \geq 1 za bilo koji x .
Ograničeno odozgo funkcija y=f(x), x \in X se poziva kada postoji broj B za koji vrijedi nejednakost f(x) \neq B za bilo koji x \in X .
Primjer funkcije ograničene ispod: y=\sqrt(1-x^(2)), x \in [-1;1] budući da je y=\sqrt(1+x^(2)) \neq 1 za bilo koji x \in [-1;1] .
Ograničeno Uobičajeno je zvati funkciju y=f(x), x \u X kada postoji broj K > 0 za koji je nejednakost \left | f(x)\desno | \neq K za bilo koji x \u X .
Primjer ograničena funkcija: y=\sin x je ograničen na cijeloj brojevnoj osi, jer \levo | \sin x \right | \neq 1.
Povećajuća i opadajuća funkcija
Uobičajeno je govoriti o funkciji koja raste na intervalu koji se razmatra kao povećanje funkcije tada, kada veća vrijednost x odgovara većoj vrijednosti funkcije y=f(x) . Slijedi da uzimajući dvije proizvoljne vrijednosti argumenta x_(1) i x_(2) iz intervala koji se razmatra, sa x_(1) > x_(2) , rezultat će biti y(x_(1)) > y(x_(2)).
Poziva se funkcija koja se smanjuje na intervalu koji se razmatra opadajuća funkcija kada veća vrijednost x odgovara manjoj vrijednosti funkcije y(x) . Iz toga slijedi da će, uzimajući iz intervala koji se razmatra, dvije proizvoljne vrijednosti argumenta x_(1) i x_(2) i x_(1) > x_(2) , rezultat biti y(x_(1))< y(x_{2}) .
Function Roots Uobičajeno je nazivati tačke u kojima funkcija F=y(x) siječe osu apscise (dobijaju se rješavanjem jednadžbe y(x)=0).
a) Ako za x > 0 parna funkcija raste, onda se smanjuje za x< 0

b) Kada se parna funkcija smanjuje na x > 0, tada raste na x< 0
.png)
c) Kada se neparna funkcija povećava na x > 0, tada raste i na x< 0

d) Kada se neparna funkcija smanji za x > 0, tada će se smanjiti i za x< 0
.png)
Ekstremi funkcije
Minimalna tačka funkcije y=f(x) se obično naziva tačka x=x_(0) čije će susjedstvo imati druge tačke (osim tačke x=x_(0)), a za njih će nejednakost f(x) > f tada biti zadovoljan (x_(0)) . y_(min) - oznaka funkcije u minimalnoj tački.
Maksimalna tačka funkcije y=f(x) se obično naziva tačka x=x_(0) čije će susjedstvo imati druge tačke (osim tačke x=x_(0)), i za njih će tada biti zadovoljena nejednakost f(x)< f(x^{0}) . y_{max} - обозначение функции в точке max.
Preduvjet
Prema Fermatovoj teoremi: f"(x)=0 kada će funkcija f(x) koja je diferencibilna u tački x_(0) imati ekstrem u ovoj tački.
Dovoljno stanje
- Kada derivacija promijeni predznak iz plusa u minus, tada će x_(0) biti minimalna tačka;
- x_(0) - biće maksimalna tačka samo kada derivacija promeni predznak sa minusa na plus kada prolazi kroz stacionarnu tačku x_(0) .
Najveća i najmanja vrijednost funkcije u intervalu
Koraci izračunavanja:
- Traži se derivacija f"(x);
- Pronalaze se stacionarne i kritične tačke funkcije i odabiru one koje pripadaju segmentu;
- Vrijednosti funkcije f(x) nalaze se na stacionarnim i kritičnim točkama i krajevima segmenta. Dobiveni rezultati će biti manji najniža vrijednost funkcije, i više - najveća.