قرار Nok 34 و 2. كيفية إيجاد المضاعف المشترك الأصغر لرقمين
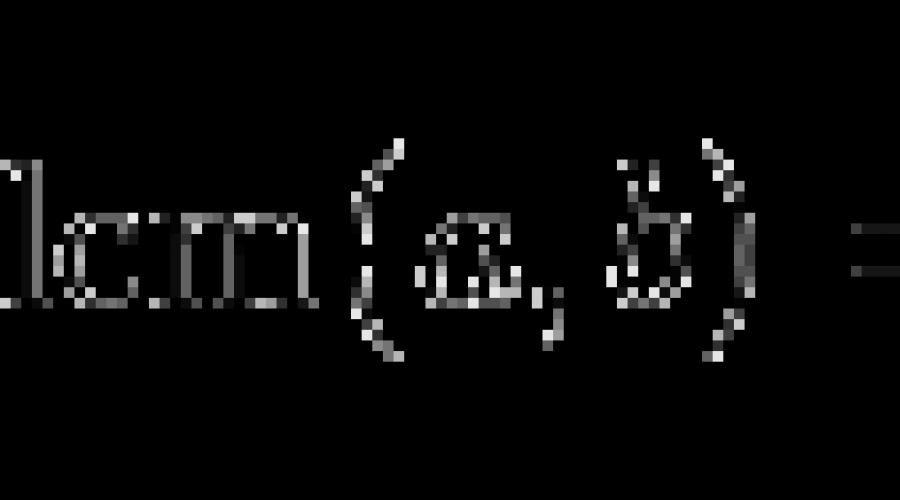
اقرأ أيضا
القاسم المشترك الأكبر والمضاعف المشترك الأصغر هما مفاهيم حسابية أساسية تسمح لك بالعمل دون عناء الكسور العادية. المضاعف المشترك الأصغر ويستخدم غالبًا لإيجاد القاسم المشترك للعديد من الكسور.
مفاهيم أساسية
المقسوم على العدد الصحيح X هو عدد صحيح آخر Y يمكن بواسطته X القسمة بدون باقي. على سبيل المثال ، القاسم على 4 هو 2 ، و 36 هو 4 ، 6 ، 9. مضاعف العدد الصحيح X هو الرقم Y الذي يقبل القسمة على X بدون باقي. على سبيل المثال ، 3 هو مضاعف 15 ، و 6 هو مضاعف 12.
يمكننا إيجاد القواسم والمضاعفات المشتركة لأي زوج من الأعداد. على سبيل المثال ، بالنسبة إلى 6 و 9 ، المضاعف المشترك هو 18 ، والمقسوم عليه المشترك هو 3. من الواضح أن الأزواج يمكن أن تحتوي على عدة قواسم ومضاعفات ، لذلك يتم استخدام القاسم الأكبر من GCD وأصغر مضاعف للمضاعف المشترك الأصغر في العمليات الحسابية .
أصغر قاسم لا معنى له ، لأنه دائمًا ما يكون واحدًا لأي رقم. المضاعف الأكبر لا معنى له أيضًا ، لأن تسلسل المضاعفات يميل إلى اللانهاية.
البحث عن GCD
توجد طرق عديدة لإيجاد القاسم المشترك الأكبر وأشهرها:
- التعداد المتسلسل للمقسومات واختيار المقسومات المشتركة للزوج والبحث عن أكبرها ؛
- تحلل الأعداد إلى عوامل غير قابلة للتجزئة ؛
- خوارزمية إقليدس
- خوارزمية ثنائية.
اليوم في المؤسسات التعليميةالطرق الأكثر شيوعًا هي التحلل إلى العوامل الأوليةوخوارزمية إقليدس. هذا الأخير ، بدوره ، يستخدم في حل معادلات ديوفانتين: البحث عن GCD مطلوب للتحقق من المعادلة لإمكانية حلها في أعداد صحيحة.
البحث عن شهادة عدم الممانعة
يتم تحديد المضاعف المشترك الأصغر أيضًا بدقة من خلال التعداد أو التحليل التكراري إلى عوامل غير قابلة للتجزئة. بالإضافة إلى ذلك ، من السهل العثور على المضاعف المشترك الأصغر إذا تم تحديد القاسم الأكبر بالفعل. بالنسبة للأرقام X و Y ، يرتبط LCM و GCD بالعلاقة التالية:
المضاعف المشترك الأصغر (X ، Y) = X × Y / GCM (X ، Y).
على سبيل المثال ، إذا كانت gcd (15،18) = 3 ، فإن المضاعف المشترك الأصغر (15،18) = 15 × 18/3 = 90. يتمثل الاستخدام الأكثر وضوحًا لـ LCM في إيجاد المقام المشترك ، وهو أقل المضاعف المشترك الكسور المعطاة.
أرقام Coprime
إذا كان زوج من الأرقام لا يحتوي على قواسم مشتركة ، فإن هذا الزوج يسمى coprime. دائمًا ما يكون GCM لمثل هذه الأزواج يساوي واحدًا ، وبناءً على اتصال القواسم والمضاعفات ، فإن GCM للجريمة المشتركة يساوي منتجهم. على سبيل المثال ، الرقمان 25 و 28 هما جريمة مشتركة ، لأنه لا يوجد بينهما قواسم مشتركة ، و LCM (25 ، 28) = 700 ، وهو ما يتوافق مع منتجهما. أي رقمين غير قابلين للتجزئة سيكونان دائمًا جريمة جماعية.
القاسم المشترك والحاسبة المتعددة
باستخدام الآلة الحاسبة الخاصة بنا ، يمكنك حساب GCD و LCM لأي عدد من الأرقام للاختيار من بينها. توجد مهام حساب القواسم والمضاعفات المشتركة في الحساب للصفين الخامس والسادس ، ومع ذلك ، فإن GCD و LCM هي المفاهيم الأساسية للرياضيات وتستخدم في نظرية الأعداد وقياس الكواكب والجبر التواصلي.
أمثلة من الحياة الواقعية
المقام المشترك للكسور
يستخدم المضاعف المشترك الأصغر عند إيجاد المقام المشترك للعديد من الكسور. افترض في مسألة حسابية أنه مطلوب جمع 5 كسور:
1/8 + 1/9 + 1/12 + 1/15 + 1/18.
لجمع كسور ، يجب اختزال التعبير إلى القاسم المشترك، مما يقلل من مشكلة إيجاد المضاعف المشترك الأصغر. للقيام بذلك ، حدد 5 أرقام في الآلة الحاسبة وأدخل قيم المقام في الخلايا المناسبة. سيحسب البرنامج المضاعف المشترك الأصغر (8 ، 9 ، 12 ، 15 ، 18) = 360. الآن أنت بحاجة إلى حساب العوامل الإضافية لكل كسر ، والتي يتم تعريفها على أنها نسبة المضاعف المشترك الأصغر إلى المقام. لذلك ستبدو المضاعفات الإضافية كما يلي:
- 360/8 = 45
- 360/9 = 40
- 360/12 = 30
- 360/15 = 24
- 360/18 = 20.
بعد ذلك ، نضرب كل الكسور في العامل الإضافي المقابل ونحصل على:
45/360 + 40/360 + 30/360 + 24/360 + 20/360.
يمكننا بسهولة إضافة هذه الكسور والحصول على النتيجة على شكل 159/360. نحن نقلل الكسر بمقدار 3 ونرى الإجابة النهائية - 53/120.
حل معادلات ديوفانتاين الخطية
معادلات ديوفانتين الخطية هي تعبيرات من الشكل ax + by = d. إذا كانت النسبة d / gcd (a، b) عددًا صحيحًا ، فإن المعادلة قابلة للحل في أعداد صحيحة. دعنا نتحقق من معادلتين لإمكانية حل عدد صحيح. أولاً ، تحقق من المعادلة 150x + 8y = 37. باستخدام الآلة الحاسبة ، نجد gcd (150.8) = 2. اقسم 37/2 = 18.5. الرقم ليس عددًا صحيحًا ، لذلك لا تحتوي المعادلة على جذور صحيحة.
دعنا نتحقق من المعادلة 1320x + 1760y = 10120. استخدم الآلة الحاسبة لإيجاد gcd (1320 ، 1760) = 440. اقسم 10120/440 = 23. نتيجة لذلك ، نحصل على عدد صحيح ، وبالتالي ، فإن معادلة ديوفنتين قابلة للحل في معاملات عدد صحيح .
خاتمة
يلعب GCD و LCM دورًا كبيرًا في نظرية الأعداد ، والمفاهيم نفسها مستخدمة على نطاق واسع في معظم الأحيان مناطق مختلفةالرياضيات. استخدم الآلة الحاسبة الخاصة بنا لحساب أكبر القواسم وأصغر مضاعفات لأي عدد من الأرقام.
لكن العديد من الأعداد الطبيعية قابلة للقسمة بالتساوي على أعداد طبيعية أخرى.
علي سبيل المثال:
الرقم 12 قابل للقسمة على 1 ، على 2 ، على 3 ، على 4 ، على 6 ، على 12 ؛
العدد 36 قابل للقسمة على 1 ، على 2 ، على 3 ، على 4 ، على 6 ، على 12 ، على 18 ، على 36.
الأرقام التي يمكن القسمة على الرقم 12 (الرقم 12 هو 1 و 2 و 3 و 4 و 6 و 12) تسمى عدد القواسم. القاسم على عدد طبيعي أهو الرقم الطبيعي الذي يقسم الرقم المحدد أدون أن يترك أثرا. يسمى الرقم الطبيعي الذي يحتوي على أكثر من عاملين مركب .
لاحظ أن العددين 12 و 36 لهما قواسم مشتركة. هذه هي الأرقام: 1 ، 2 ، 3 ، 4 ، 6 ، 12. أكبر قاسم على هذه الأرقام هو 12. القاسم المشترك لهذين العددين أو بهو الرقم الذي يمكن به القسمة على كلا الرقمين المعينين بدون باقي أو ب.
المضاعف المشتركعدة أرقام تسمى الرقم الذي يقبل القسمة على كل من هذه الأرقام. علي سبيل المثال، فإن المضاعف المشترك للأرقام 9 و 18 و 45 هو 180. لكن 90 و 360 هما أيضًا مضاعفاتهما المشتركة. من بين جميع مضاعفات jcommon ، هناك دائمًا الأصغر ، in هذه القضيةإنه 90. هذا الرقم يسمى الأقلالمضاعف المشترك (LCM).
دائمًا ما يكون المضاعف المشترك الأصغر عددًا طبيعيًا ، والذي يجب أن يكون أكبر من أكبر الأرقام التي تم تحديدها من أجلها.
المضاعف المشترك الأصغر (LCM). ملكيات.
التبادلية:
الترابطية:
![]()
على وجه الخصوص ، إذا كانت وأرقام حقوق الملكية الفكرية ، إذن:
المضاعف المشترك الأصغر لعددين صحيحين مو نهو القاسم على جميع المضاعفات المشتركة الأخرى مو ن. علاوة على ذلك ، مجموعة المضاعفات المشتركة م ، نيتطابق مع مجموعة مضاعفات المضاعف المشترك الأصغر ( م ، ن).
يمكن التعبير عن مقاربات من حيث عدد الوظائف النظرية.
لذا، وظيفة Chebyshev. إلى جانب:
هذا يتبع من تعريف وخصائص وظيفة لانداو ز (ن).
ما يلي من قانون توزيع الأعداد الأولية.
إيجاد المضاعف المشترك الأصغر.
شهادة عدم ممانعة ( أ ، ب) بعدة طرق:
1. إذا كان القاسم المشترك الأكبر معروفًا ، فيمكنك استخدام علاقته مع المضاعف المشترك الأصغر:
![]()
2. دع التحليل القانوني لكلا العددين إلى عوامل أولية معروفًا:
![]()
أين ص 1 ، ... ، ص ك- متنوع الأعداد الأولية، أ د 1 ، ... ، د كو ه 1 ، ... ، إلخهي أعداد صحيحة غير سالبة (يمكن أن تكون صفراً إذا لم يكن العدد الأولي المقابل في حالة التحلل).
ثم LCM ( أ,ب) حسب الصيغة:
بمعنى آخر ، يحتوي توسع المضاعف المشترك الأصغر على جميع العوامل الأولية المضمنة في واحد على الأقل من توسعات الأرقام أ ، ب، ويتم أخذ أكبر الأسين لهذا العامل.
مثال:
يمكن اختزال حساب المضاعف المشترك الأصغر لعدة أرقام إلى عدة حسابات متتالية للمضاعف المشترك الأصغر لرقمين:
القاعدة.للعثور على المضاعف المشترك الأصغر لسلسلة من الأرقام ، تحتاج إلى:
- تحلل الأرقام إلى عوامل أولية ؛
- تحويل التوسع الأكبر إلى عوامل المنتج المطلوب (ناتج عوامل عدد كبيرمن الأرقام المعطاة) ، ثم أضف عوامل من تحلل الأرقام الأخرى التي لا تحدث في الرقم الأول أو تكون فيه عددًا أقل من المرات ؛
- حاصل ضرب العوامل الأولية الناتج سيكون المضاعف المشترك الأصغر للأرقام المعطاة.
أي اثنين أو أكثر الأعداد الطبيعيةلديهم شهادة عدم ممانعة خاصة بهم. إذا لم تكن الأرقام مضاعفات لبعضها البعض أو لم يكن لها نفس العوامل في التوسع ، فإن المضاعف المشترك الأصغر الخاص بها يساوي حاصل ضرب هذه الأرقام.

تم استكمال العوامل الأولية للعدد 28 (2 ، 2 ، 7) بعامل 3 (الرقم 21) ، المنتج الناتج (84) سيكون أصغر رقم، والتي تقبل القسمة على 21 و 28.

تم استكمال العوامل الأولية لأكبر رقم 30 بمعامل 5 من الرقم 25 ، والمنتج الناتج 150 أكبر من أكبر رقم 30 وقابل للقسمة على جميع الأرقام المعطاة بدون باقي. هذا هو أصغر منتج ممكن (150 ، 250 ، 300 ...) تكون جميع الأرقام المعطاة من مضاعفاته.

الأعداد 2،3،11،37 أولية ، لذا فإن المضاعف المشترك الأصغر الخاص بها يساوي حاصل ضرب الأعداد المعطاة.
القاعدة. لحساب المضاعف المشترك الأصغر للأعداد الأولية ، عليك ضرب كل هذه الأعداد معًا.
خيار اخر:
للعثور على المضاعف المشترك الأصغر (LCM) لعدة أرقام تحتاجها:
1) تمثل كل رقم كمنتج من عوامله الأولية ، على سبيل المثال:
504 \ u003d 2 2 2 3 3 7 ،
2) اكتب قوى جميع العوامل الأولية:
504 \ u003d 2 2 2 3 3 7 \ u003d 2 3 3 2 7 1 ،
3) اكتب جميع القواسم الأولية (المضاعفات) لكل من هذه الأرقام ؛
4) اختر الدرجة الأكبر لكل منهم والموجودة في جميع توسعات هذه الأرقام ؛
5) اضرب هذه القوى.
مثال. أوجد المضاعف المشترك الأصغر للأرقام: 168 ، 180 ، 3024.
قرار. 168 \ u003d 2 2 2 3 7 \ u003d 2 3 3 1 7 1 ،
180 \ u003d 2 2 3 3 5 \ u003d 2 2 3 2 5 1 ،
3024 = 2 2 2 2 3 3 3 7 = 2 4 3 3 7 1.
نكتب أكبر قوى لجميع القواسم الأولية ونضربها:
المضاعف المشترك الأصغر = 2 4 3 3 5 1 7 1 = 15120.
مضاعف الرقم هو رقم يقبل القسمة على رقم معين بدون باقي. المضاعف المشترك الأصغر (LCM) لمجموعة من الأرقام هو أصغر رقم يقبل القسمة بالتساوي على كل رقم في المجموعة. لإيجاد المضاعف المشترك الأصغر ، عليك إيجاد العوامل الأولية للأرقام المحددة. أيضًا ، يمكن حساب المضاعف المشترك الأصغر باستخدام عدد من الطرق الأخرى التي تنطبق على مجموعات مكونة من رقمين أو أكثر.
خطوات
عدد من المضاعفات
- على سبيل المثال ، ابحث عن المضاعف المشترك الأصغر للعددين 5 و 8. فهذان عددان صغيران ، لذا يمكن استخدام هذه الطريقة.
-
مضاعف الرقم هو رقم يقبل القسمة على رقم معين بدون باقي. يمكن العثور على أرقام متعددة في جدول الضرب.
- على سبيل المثال ، الأرقام التي تكون من مضاعفات العدد 5 هي: 5 ، 10 ، 15 ، 20 ، 25 ، 30 ، 35 ، 40.
-
اكتب سلسلة من الأعداد على شكل مضاعفات العدد الأول.افعل ذلك ضمن مضاعفات الرقم الأول لمقارنة صفين من الأرقام.
- على سبيل المثال ، الأرقام التي تكون مضاعفات 8 هي: 8 و 16 و 24 و 32 و 40 و 48 و 56 و 64.
-
أوجد أصغر عدد يظهر في سلسلتي المضاعفات.قد تضطر إلى كتابة سلسلة طويلة من المضاعفات للعثور عليها الرقم الإجمالي. أصغر رقم يظهر في سلسلتي المضاعفات هو المضاعف المشترك الأصغر.
- على سبيل المثال ، أصغر رقم يظهر في سلسلة مضاعفات الرقمين 5 و 8 هو 40. لذلك ، فإن 40 هو المضاعف المشترك الأصغر للعددين 5 و 8.
التحليل الأولي
-
انظر إلى هذه الأرقام.يتم استخدام الطريقة الموصوفة هنا بشكل أفضل عند إعطاء رقمين أكبر من 10. إذا تم تقديم أرقام أصغر ، فاستخدم طريقة مختلفة.
- على سبيل المثال ، ابحث عن المضاعف المشترك الأصغر للعددين 20 و 84. كل رقم أكبر من 10 ، لذلك يمكن استخدام هذه الطريقة.
-
حلل الرقم الأول إلى عوامل.أي أنك تحتاج إلى إيجاد مثل هذه الأعداد الأولية ، عند ضربها ، تحصل على رقم معين. بعد أن وجدت العوامل الأولية ، اكتبها كمساواة.
- علي سبيل المثال، 2 × 10 = 20 (\ displaystyle (\ mathbf (2)) \ times 10 = 20)و 2 × 5 = 10 (\ displaystyle (\ mathbf (2)) \ times (\ mathbf (5)) = 10). إذن ، العوامل الأولية للعدد 20 هي الأعداد 2 و 2 و 5. اكتبهم على هيئة تعبير:.
-
حلل الرقم الثاني إلى عوامل أولية.افعل ذلك بالطريقة نفسها التي حللت بها الرقم الأول إلى عوامل ، أي أوجد مثل هذه الأعداد الأولية التي ، عند ضربها ، ستحصل على هذا العدد.
- علي سبيل المثال، 2 × 42 = 84 (\ displaystyle (\ mathbf (2)) \ times 42 = 84), 7 × 6 = 42 (\ displaystyle (\ mathbf (7)) \ times 6 = 42)و 3 × 2 = 6 (\ displaystyle (\ mathbf (3)) \ times (\ mathbf (2)) = 6). إذن ، العوامل الأولية للعدد 84 هي الأعداد 2 و 7 و 3 و 2. اكتبهم على شكل تعبير:.
-
اكتب العوامل المشتركة لكلا العددين.اكتب هذه العوامل مثل عملية الضرب. أثناء كتابة كل عامل ، اشطبه في كلا التعبيرين (التعبيرات التي تصف تحلل الأعداد إلى عوامل أولية).
- على سبيل المثال ، العامل المشترك لكلا العددين هو 2 ، لذا اكتب 2 × (displaystyle 2 times)واشطب الرقم 2 في كلا التعبيرين.
- العامل المشترك لكلا العددين هو عامل آخر للعدد 2 ، لذا اكتب 2 × 2 (\ displaystyle 2 \ times 2)واشطب 2 في كلا التعبيرين.
-
أضف العوامل المتبقية إلى عملية الضرب.هذه عوامل لم يتم شطبها في كلا التعبيرين ، أي عوامل غير مشتركة لكلا الرقمين.
- على سبيل المثال ، في التعبير 20 = 2 × 2 × 5 (\ displaystyle 20 = 2 \ times 2 \ times 5)تم شطب كلا الاثنين (2) لأنهما عاملين مشتركين. لم يتم شطب العامل 5 ، لذا اكتب عملية الضرب على النحو التالي: 2 × 2 × 5 (\ displaystyle 2 \ times 2 \ times 5)
- في التعبير 84 = 2 × 7 × 3 × 2 (\ displaystyle 84 = 2 \ times 7 \ times 3 \ times 2)كلا التعادلين (2) تم شطبهما. لم يتم شطب العاملين 7 و 3 ، لذلك اكتب عملية الضرب على النحو التالي: 2 × 2 × 5 × 7 × 3 (\ displaystyle 2 \ times 2 \ times 5 \ times 7 \ times 3).
-
احسب المضاعف المشترك الأصغر.للقيام بذلك ، اضرب الأرقام في عملية الضرب المكتوبة.
- علي سبيل المثال، 2 × 2 × 5 × 7 × 3 = 420 (\ displaystyle 2 \ times 2 \ times 5 \ times 7 \ times 3 = 420). إذن ، المضاعف المشترك الأصغر للعددين 20 و 84 هو 420.
إيجاد القواسم المشتركة
-
ارسم شبكة كما تفعل في لعبة تيك تاك تو.تتكون هذه الشبكة من خطين متوازيين يتقاطعان (بزوايا قائمة) مع خطين متوازيين آخرين. سينتج عن ذلك ثلاثة صفوف وثلاثة أعمدة (تشبه الشبكة إلى حد كبير علامة #). اكتب الرقم الأول في الصف الأول والعمود الثاني. اكتب الرقم الثاني في الصف الأول والعمود الثالث.
- على سبيل المثال ، أوجد المضاعف المشترك الأصغر بين 18 و 30. اكتب 18 في الصف الأول والعمود الثاني ، واكتب 30 في الصف الأول والعمود الثالث.
-
أوجد القاسم المشترك لكلا العددين.اكتبها في الصف الأول والعمود الأول. من الأفضل البحث عن قواسم أولية ، لكن هذا ليس شرطًا أساسيًا.
- على سبيل المثال ، 18 و 30 أعداد زوجية ، لذا فإن القاسم المشترك بينهما هو 2. لذا اكتب 2 في الصف الأول والعمود الأول.
-
قسّم كل رقم على القاسم الأول.اكتب كل حاصل تحت الرقم المقابل. حاصل القسمة هو نتيجة قسمة رقمين.
- علي سبيل المثال، 18 ÷ 2 = 9 (\ displaystyle 18 \ div 2 = 9)، لذلك اكتب 9 تحت سن 18.
- 30 ÷ 2 = 15 (\ displaystyle 30 \ div 2 = 15)، لذلك اكتب 15 تحت 30.
-
أوجد القاسم المشترك لكلا خارج القسمة.إذا لم يكن هناك قاسم من هذا القبيل ، فتخط الخطوتين التاليتين. وإلا فاكتب المقسوم عليه في الصف الثاني والعمود الأول.
- على سبيل المثال ، 9 و 15 يقبلان القسمة على 3 ، لذا اكتب 3 في الصف الثاني والعمود الأول.
-
اقسم كل حاصل على القاسم الثاني.اكتب كل نتيجة قسمة تحت حاصل القسمة المقابل.
- علي سبيل المثال، 9 ÷ 3 = 3 (\ displaystyle 9 \ div 3 = 3)، لذلك اكتب 3 تحت 9.
- 15 ÷ 3 = 5 (\ displaystyle 15 \ div 3 = 5)، لذا اكتب 5 تحت 15.
-
إذا لزم الأمر ، استكمل الشبكة بخلايا إضافية.كرر الخطوات السابقة حتى تحصل على قسمة مشتركة.
-
ضع دائرة حول الأرقام الموجودة في العمود الأول والصف الأخير من الشبكة.ثم اكتب الأرقام المميزة كعملية ضرب.
- على سبيل المثال ، الرقمان 2 و 3 موجودان في العمود الأول ، والأرقام 3 و 5 في الصف الأخير ، لذلك اكتب عملية الضرب على النحو التالي: 2 × 3 × 3 × 5 (\ displaystyle 2 \ times 3 \ times 3 \ times 5).
-
أوجد نتيجة ضرب الأعداد.سيحسب هذا المضاعف المشترك الأصغر بين عددين محددين.
- علي سبيل المثال، 2 × 3 × 3 × 5 = 90 (\ displaystyle 2 \ times 3 \ times 3 \ times 5 = 90). إذن ، المضاعف المشترك الأصغر للعددين 18 و 30 هو 90.
خوارزمية إقليدس
-
تذكر المصطلحات المرتبطة بعملية التقسيم.المقسوم هو الرقم الذي يتم تقسيمه. القاسم هو الرقم المطلوب القسمة عليه. حاصل القسمة هو نتيجة قسمة رقمين. الباقي هو الرقم المتبقي عند قسمة رقمين.
- على سبيل المثال ، في التعبير 15 ÷ 6 = 2 (\ displaystyle 15 \ div 6 = 2)راحة. 3:
15 هو الذي يقبل القسمة
6 هو القاسم
2 خاص
3 هو الباقي.
- على سبيل المثال ، في التعبير 15 ÷ 6 = 2 (\ displaystyle 15 \ div 6 = 2)راحة. 3:
انظر إلى هذه الأرقام.الطريقة الموصوفة هنا هي أفضل استخدام عند إعطاء رقمين كلاهما أقل من 10. إذا تم تقديم أعداد كبيرة ، فاستخدم طريقة مختلفة.
المواد أدناه استمرار منطقينظريات من المقالة بعنوان LCM - المضاعف المشترك الأصغر ، التعريف ، الأمثلة ، العلاقة بين LCM و GCM. هنا سنتحدث عن إيجاد المضاعف المشترك الأصغر (LCM)، و انتباه خاصدعنا نلقي نظرة على الأمثلة. دعونا أولاً نوضح كيف يتم حساب المضاعف المشترك الأصغر لرقمين من حيث GCD لهذه الأرقام. بعد ذلك ، ضع في اعتبارك إيجاد المضاعف المشترك الأصغر عن طريق تحليل الأعداد إلى عوامل أولية. بعد ذلك ، سنركز على إيجاد المضاعف المشترك الأصغر لثلاثة و أكثرالأرقام ، وانتبه أيضًا إلى حساب المضاعف المشترك الأصغر للأرقام السالبة.
التنقل في الصفحة.
حساب المضاعف المشترك الأصغر (LCM) من خلال gcd
تعتمد إحدى طرق العثور على المضاعف المشترك الأصغر على العلاقة بين LCM و GCD. تسمح لك العلاقة الحالية بين LCM و GCD بحساب المضاعف المشترك الأصغر لعددين صحيحين موجبين من خلال القاسم المشترك الأكبر المعروف. الصيغة المقابلة لها الشكل المضاعف المشترك الأصغر (أ ، ب) = أ ب: GCD (أ ، ب) . ضع في اعتبارك أمثلة لإيجاد المضاعف المشترك الأصغر وفقًا للصيغة أعلاه.
مثال.
أوجد المضاعف المشترك الأصغر للعددين 126 و 70.
قرار.
في هذا المثال أ = 126 ، ب = 70. دعونا نستخدم العلاقة بين LCM و GCD التي تعبر عنها الصيغة المضاعف المشترك الأصغر (أ ، ب) = أ ب: GCD (أ ، ب). أي ، علينا أولاً إيجاد القاسم المشترك الأكبر للعددين 70 و 126 ، وبعد ذلك يمكننا حساب المضاعف المشترك الأصغر لهذين العددين وفقًا للصيغة المكتوبة.
أوجد gcd (126، 70) باستخدام خوارزمية إقليدس: 126 = 70 1 + 56، 70 = 56 1 + 14، 56 = 14 4 ، وبالتالي gcd (126، 70) = 14.
الآن نجد المضاعف المشترك الأصغر المطلوب: المضاعف المشترك الأصغر (126 ، 70) = 126 70: المضاعف المشترك الأصغر (126 ، 70) = 126 70: 14 = 630.
إجابه:
المضاعف المشترك الأصغر (126 ، 70) = 630.
مثال.
ما هو LCM (68 ، 34)؟
قرار.
مثل 68 يقبل القسمة على 34 بالتساوي ، ثم gcd (68 ، 34) = 34. الآن نحسب المضاعف المشترك الأصغر: المضاعف المشترك الأصغر (68، 34) = 68 34: المضاعف المشترك الأصغر (68، 34) = 68 34: 34 = 68.
إجابه:
المضاعف المشترك الأصغر (68 ، 34) = 68.
لاحظ أن المثال السابق يناسب القاعدة التالية لإيجاد المضاعف المشترك الأصغر للأعداد الصحيحة الموجبة أ وب: إذا كان الرقم أ قابل للقسمة على ب ، فإن المضاعف المشترك الأصغر لهذه الأرقام هو أ.
إيجاد المضاعف المشترك الأصغر عن طريق تحليل الأرقام إلى العوامل الأولية
طريقة أخرى لإيجاد المضاعف المشترك الأصغر تعتمد على تحليل الأعداد إلى عوامل أولية. إذا صنعنا منتجًا لجميع العوامل الأولية لهذه الأرقام ، وبعد ذلك نستبعد من هذا المنتج جميع العوامل الأولية المشتركة الموجودة في توسعات هذه الأرقام ، فسيكون المنتج الناتج مساويًا للمضاعف المشترك الأصغر لهذه الأرقام.
القاعدة المعلنة لإيجاد المضاعف المشترك الأصغر تأتي من المساواة المضاعف المشترك الأصغر (أ ، ب) = أ ب: GCD (أ ، ب). في الواقع ، حاصل ضرب العددين a و b يساوي حاصل ضرب جميع العوامل المشاركة في تمددات العددين a و b. في المقابل ، gcd (أ ، ب) يساوي حاصل ضرب جميع العوامل الأولية الموجودة في نفس الوقت في توسعات الأرقام أ وب (الموصوفة في القسم الخاص بإيجاد gcd باستخدام تحليل الأرقام إلى عوامل أولية ).
لنأخذ مثالا. لنعلم أن 75 = 3 5 5 و 210 = 2 3 5 7. لنصنع منتجًا من جميع عوامل هذه التوسعات: 2 3 3 5 5 5 7. نستبعد الآن من هذا المنتج جميع العوامل الموجودة في توسيع الرقم 75 وفي توسيع الرقم 210 (هذه العوامل هي 3 و 5) ، ثم يأخذ المنتج الشكل 2 3 5 5 7. قيمة هذا المنتج تساوي المضاعف المشترك الأصغر للأرقام 75 و 210 ، أي ، المضاعف المشترك الأصغر (75 ، 210) = 2 3 5 5 7 = 1050.
مثال.
بعد تحليل العددين 441 و 700 إلى عوامل أولية ، أوجد المضاعف المشترك الأصغر لهذه الأعداد.
قرار.
لنحلل العددين 441 و 700 إلى عوامل أولية:
نحصل على 441 = 3 3 7 7 و 700 = 2 2 5 5 7.
لنصنع الآن حاصل ضرب جميع العوامل التي تدخل في فساد هذه الأعداد: 2 2 3 3 5 5 7 7 7. دعنا نستبعد من هذا المنتج جميع العوامل الموجودة في وقت واحد في كلا التوسيعين (يوجد عامل واحد فقط - هذا هو الرقم 7): 2 2 3 3 5 5 7 7. هكذا، المضاعف المشترك الأصغر (441، 700) = 2 2 3 3 5 5 7 7 = 44100.
إجابه:
المضاعف المشترك الأصغر (441 ، 700) = 44100.
يمكن صياغة قاعدة إيجاد المضاعف المشترك الأصغر باستخدام تحليل الأعداد إلى عوامل أولية بشكل مختلف قليلاً. إذا أضفنا العوامل المفقودة من توسيع الرقم b إلى العوامل من توسيع الرقم a ، فإن قيمة المنتج الناتج ستكون مساوية للمضاعف المشترك الأصغر للأرقام a و b.
على سبيل المثال ، لنأخذ جميع الأعداد نفسها 75 و 210 ، فوسعاتهم إلى العوامل الأولية هي كما يلي: 75 = 3 5 5 و 210 = 2 3 5 7. إلى العوامل 3 و 5 و 5 من تحلل الرقم 75 ، نضيف العوامل الناقصة 2 و 7 من تحلل الرقم 210 ، نحصل على الناتج 2 3 5 5 7 ، الذي قيمته هو المضاعف المشترك الأصغر (75) ، 210).
مثال.
أوجد المضاعف المشترك الأصغر للرقمين 84 و 648.
قرار.
نحصل أولاً على تحليل العددين 84 و 648 إلى عوامل أولية. تبدو مثل 84 = 2 2 3 7 و 648 = 2 2 2 3 3 3 3. إلى العوامل 2 و 2 و 3 و 7 من تحلل الرقم 84 نضيف العوامل المفقودة 2 و 3 و 3 و 3 من تحلل الرقم 648 ، نحصل على الناتج 2 2 2 3 3 3 3 7 ، وهو ما يساوي 4536. وبالتالي ، فإن المضاعف المشترك الأصغر المطلوب للعددين 84 و 648 هو 4،536.
إجابه:
المضاعف المشترك الأصغر (84، 648) = 4536.
إيجاد المضاعف المشترك الأصغر لثلاثة أرقام أو أكثر
يمكن إيجاد المضاعف المشترك الأصغر لثلاثة أرقام أو أكثر عن طريق إيجاد المضاعف المشترك الأصغر لرقمين على التوالي. تذكر النظرية المقابلة ، والتي تعطي طريقة لإيجاد المضاعف المشترك الأصغر لثلاثة أرقام أو أكثر.
نظرية.
لنفترض أن الأعداد الصحيحة الموجبة أ 1 ، أ 2 ، ... ، أ ك تُعطى ، المضاعف المشترك الأصغر م ك لهذه الأرقام موجود في الحساب المتسلسل م 2 = المضاعف المشترك الأصغر (أ 1 ، أ 2) ، م 3 = المضاعف المشترك الأصغر (م 2 ، أ 3) ، ... ، م ك = المضاعف المشترك الأصغر (م ك − 1 ، أ ك).
ضع في اعتبارك تطبيق هذه النظرية في مثال إيجاد المضاعف المشترك الأصغر لأربعة أرقام.
مثال.
أوجد المضاعف المشترك الأصغر للأعداد الأربعة 140 و 9 و 54 و 250.
قرار.
في هذا المثال ، 1 = 140 ، 2 = 9 ، 3 = 54 ، 4 = 250.
أولا نجد م 2 \ u003d م م 2 (أ 1 ، أ 2) \ u003d م م 2 (140 ، 9). للقيام بذلك ، باستخدام الخوارزمية الإقليدية ، نحدد gcd (140 ، 9) ، لدينا 140 = 9 15 + 5 ، 9 = 5 1 + 4 ، 5 = 4 1 + 1 ، 4 = 1 4 ، لذلك ، gcd ( 140 ، 9) = 1 من أين المضاعف المشترك الأصغر (140 ، 9) = 140 9: المضاعف المشترك الأصغر (140 ، 9) = 140 9: 1 = 1260. أي م 2 = 1260.
الآن نجد م 3 \ u003d م.س.م (م 2 ، أ 3) \ u003d م.س. (1260 ، 54). دعونا نحسبها من خلال gcd (1260 ، 54) ، والتي تحددها أيضًا خوارزمية إقليدس: 1260 = 54 23 + 18 ، 54 = 18 3. ثم gcd (1260 ، 54) = 18 ، من أين LCM (1260 ، 54) = 1260 54: gcd (1260 ، 54) = 1260 54: 18 = 3780. أي م 3 = 3780.
تركت لتجد م 4 \ u003d م م 3 (م 3 ، أ 4) \ u003d م م 3 (3780 ، 250). للقيام بذلك ، نجد GCD (3780 ، 250) باستخدام خوارزمية إقليدس: 3780 = 250 15 + 30 ، 250 = 30 8 + 10 ، 30 = 10 3. لذلك ، gcd (3780 ، 250) = 10 ، ومن أين gcd (3780 ، 250) = 3780250: gcd (3780، 250) = 3780250: 10 = 94500. أي م 4 = 94500.
إذن ، المضاعف المشترك الأصغر للأعداد الأربعة الأصلية هو 94500.
إجابه:
المضاعف المشترك الأصغر (140، 9، 54، 250) = 94،500.
في كثير من الحالات ، يمكن العثور بسهولة على المضاعف المشترك الأصغر لثلاثة أرقام أو أكثر باستخدام التحليل الأولي لأرقام معينة. في هذه الحالة ، يجب اتباع القاعدة التالية. المضاعف المشترك الأصغر لعدة أرقام يساوي المنتج ، والذي يتكون على النحو التالي: تضاف العوامل المفقودة من توسيع الرقم الثاني إلى جميع العوامل من توسيع الرقم الأول ، والعوامل المفقودة من توسيع الرقم الأول يضاف الرقم الثالث إلى العوامل التي تم الحصول عليها ، وهكذا.
ضع في اعتبارك مثالًا لإيجاد المضاعف المشترك الأصغر باستخدام تحليل الأرقام إلى عوامل أولية.
مثال.
أوجد المضاعف المشترك الأصغر لخمسة أعداد 84 ، 6 ، 48 ، 7 ، 143.
قرار.
أولاً ، نحصل على توسعات هذه الأعداد إلى عوامل أولية: 84 = 2 2 3 7 ، 6 = 2 3 ، 48 = 2 2 2 2 3 ، 7 عوامل أولية) و 143 = 11 13.
لإيجاد المضاعف المشترك الأصغر لهذه الأعداد ، تحتاج إلى إضافة العوامل المفقودة من توسيع العدد الثاني 6 إلى عوامل العدد الأول 84 (وهي 2 و 2 و 3 و 7). لا يحتوي توسيع الرقم 6 على عوامل مفقودة ، حيث إن كلا من 2 و 3 موجودان بالفعل في توسيع الرقم الأول 84. بالإضافة إلى العوامل 2 و 2 و 3 و 7 نضيف العوامل المفقودة 2 و 2 من توسيع الرقم الثالث 48 ، نحصل على مجموعة من العوامل 2 و 2 و 2 و 2 و 3 و 7. ليست هناك حاجة لإضافة عوامل إلى هذه المجموعة في الخطوة التالية ، حيث تم تضمين 7 بالفعل فيها. أخيرًا ، إلى العوامل 2 و 2 و 2 و 2 و 3 و 7 نضيف العوامل المفقودة 11 و 13 من مفكوك العدد 143. نحصل على حاصل الضرب 2 2 2 2 3 7 11 13 ، وهو ما يساوي 48 048.
القاسم المشترك الأكبر
التعريف 2
إذا كان الرقم الطبيعي a قابل للقسمة على رقم طبيعي $ b $ ، فإن $ b $ يسمى قاسمه $ a $ ، والرقم $ a $ يسمى مضاعف $ b $.
لنفترض أن $ a $ و $ b $ هما عددان طبيعيان. الرقم $ c $ يسمى القاسم المشترك لكل من $ a $ و $ b $.
مجموعة القواسم المشتركة للأرقام $ a $ و $ b $ محدودة ، حيث لا يمكن أن يكون أي من هذه القواسم أكبر من $ a $. هذا يعني أنه من بين هذه القواسم ، يوجد أكبر واحد ، والذي يسمى القاسم المشترك الأكبر للأرقام $ a $ و $ b $ ، ويتم استخدام الترميز للدلالة عليه:
$ gcd \ (a؛ b) \ or \ D \ (a؛ b) $
لإيجاد القاسم المشترك الأكبر لرقمين:
- ابحث عن حاصل ضرب الأرقام الموجودة في الخطوة 2. سيكون الرقم الناتج هو القاسم المشترك الأكبر المطلوب.
مثال 1
أوجد gcd للأرقام $ 121 و $ 132. $
242 دولارًا = 2 \ cdot 11 \ cdot 11 دولارًا
132 دولار = 2 \ cdot 2 \ cdot 3 \ cdot 11 دولار
اختر الأرقام التي تم تضمينها في توسيع هذه الأرقام
242 دولارًا = 2 \ cdot 11 \ cdot 11 دولارًا
132 دولار = 2 \ cdot 2 \ cdot 3 \ cdot 11 دولار
ابحث عن حاصل ضرب الأرقام الموجودة في الخطوة 2. سيكون الرقم الناتج هو القاسم المشترك الأكبر المطلوب.
$ gcd = 2 \ cdot 11 = 22 دولار
مثال 2
أوجد GCD للأحادية 63 دولارًا و 81 دولارًا.
سنجد وفقًا للخوارزمية المقدمة. لهذا:
دعونا نحلل الأعداد إلى عوامل أولية
63 دولارًا = 3 \ cdot 3 \ cdot 7 دولار
81 دولارًا = 3 \ cdot 3 \ cdot 3 \ cdot 3 $
نختار الأرقام التي يتم تضمينها في توسيع هذه الأرقام
63 دولارًا = 3 \ cdot 3 \ cdot 7 دولار
81 دولارًا = 3 \ cdot 3 \ cdot 3 \ cdot 3 $
لنجد حاصل ضرب الأرقام الموجودة في الخطوة 2. سيكون الرقم الناتج هو القاسم المشترك الأكبر المطلوب.
$ gcd = 3 \ cdot 3 = 9 $
يمكنك إيجاد GCD لرقمين بطريقة أخرى ، باستخدام مجموعة قواسم الأعداد.
مثال 3
أوجد gcd للأرقام 48 دولارًا و 60 دولارًا.
قرار:
ابحث عن مجموعة المقسومات بـ 48 $: $ \ left \ ((\ rm 1،2،3.4.6،8،12،16،24،48) \ right \) $
لنجد الآن مجموعة القواسم 60 دولارًا: $ \ left \ ((\ rm 1،2،3،4،5،6،10،12،15،20،30،60) \ right \) $
لنجد تقاطع هذه المجموعات: $ \ left \ ((\ rm 1،2،3،4،6،12) \ right \) $ - ستحدد هذه المجموعة مجموعة القواسم المشتركة للأرقام $ 48 و $ 60 $. أكبر عنصر في مجموعة معينةسيكون الرقم $ 12 $. إذن ، فإن القاسم المشترك الأكبر بين 48 دولارًا و 60 دولارًا هو 12 دولارًا.
تعريف شهادة عدم الممانعة
التعريف 3
المضاعف المشترك للأعداد الطبيعية$ a $ و $ b $ رقم طبيعي من مضاعفات كل من $ a $ و $ b $.
المضاعفات الشائعة للأرقام هي الأرقام التي تقبل القسمة على الأصل دون الباقي. على سبيل المثال ، بالنسبة للأرقام 25 دولارًا و 50 دولارًا ، ستكون المضاعفات المشتركة هي الأرقام 50،100،150،200 دولار ، إلخ.
يُطلق على المضاعف المشترك الأصغر اسم المضاعف المشترك الأصغر ويُشار إليه بواسطة LCM $ (a؛ b) $ أو K $ (a؛ b). $
للعثور على المضاعف المشترك الأصغر لرقمين ، تحتاج إلى:
- حلل الأعداد إلى عوامل أولية
- اكتب العوامل التي تشكل جزءًا من الرقم الأول وأضف إليها العوامل التي تشكل جزءًا من الثاني ولا تنتقل إلى الأول
مثال 4
أوجد المضاعف المشترك الأصغر للأرقام 99 $ و 77 $.
سنجد وفقًا للخوارزمية المقدمة. لهذا
حلل الأعداد إلى عوامل أولية
99 دولارًا = 3 \ cdot 3 \ cdot 11 دولارًا
اكتب العوامل المدرجة في الأول
أضف إليهم العوامل التي هي جزء من الثانية ولا تذهب إلى الأول
ابحث عن حاصل ضرب الأرقام الموجودة في الخطوة 2. سيكون الرقم الناتج هو المضاعف المشترك الأصغر المطلوب
$ LCC = 3 \ cdot 3 \ cdot 11 \ cdot 7 = 693 دولار
غالبًا ما يستغرق تجميع قوائم قواسم الأرقام وقتًا طويلاً. هناك طريقة للعثور على GCD تسمى خوارزمية إقليدس.
العبارات التي تستند إليها خوارزمية إقليدس:
إذا كان $ a $ و $ b $ من الأعداد الطبيعية ، و $ a \ vdots b $ ، فإن $ D (a؛ b) = b $
إذا كان $ a $ و $ b $ من الأعداد الطبيعية مثل $ b
باستخدام $ D (a؛ b) = D (a-b؛ b) $ ، يمكننا خفض الأرقام قيد الدراسة على التوالي حتى نصل إلى زوج من الأرقام بحيث يكون أحدهما قابلاً للقسمة على الآخر. ثم سيكون أصغر هذه الأرقام هو القاسم المشترك الأكبر المطلوب للأرقام $ a $ و $ b $.
خصائص GCD و LCM
- أي مضاعف مشترك لـ $ a $ و $ b $ يقبل القسمة على K $ (a؛ b) $
- إذا كان $ a \ vdots b $ ، فإن K $ (a؛ b) = a $
إذا كان K $ (a؛ b) = k $ و $ m $ - رقم طبيعي ، فإن K $ (am؛ bm) = km $
إذا كان $ d $ قاسمًا شائعًا لـ $ a $ و $ b $ ، فإن K ($ \ frac (a) (d)؛ \ frac (b) (d) $) = $ \ \ frac (k) (d ) $
إذا كان $ a \ vdots c $ و $ b \ vdots c $ ، فإن $ \ frac (ab) (c) $ هو مضاعف مشترك لـ $ a $ و $ b $
لأية أرقام طبيعية $ a $ و $ b $ تساوي المساواة
$ D (a؛ b) \ cdot K (a؛ b) = ab $
أي قاسم مشترك لـ $ a $ و $ b $ هو قاسمه $ D (a؛ b) $